Engage NY Eureka Math 6th Grade Module 3 Lesson 6 Answer Key
Eureka Math Grade 6 Module 3 Lesson 6 Example Answer Key
Example 1.
If b is a nonzero whole number, then the unit fraction \(\frac{1}{b}\) is located on the number line by dividing the segment between 0 and 1 into b segments of equal length. One of the b segments has 0 as its left end point; the right end point of this segment corresponds to the unit fraction \(\frac{1}{b}\).
Answer:
→ Since the number is a rational number, a number that can be represented as a fraction, determine how the number line should be scaled.1
→ First, divide the number line into two halves to represent positive and negative numbers.
Have students complete this task on their student pages.
→ Next, divide the right half of the number line segment between 0 and 1 into ten segments of equal length; each segment has a length of \(\frac{1}{10}\).
Students divide their number lines into ten equal segments as shown. Check for accuracy.
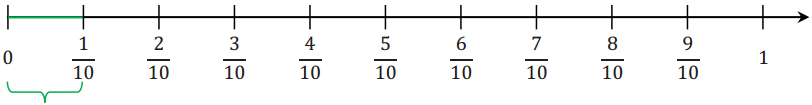
There are 10 equal segments. Each segment has a length of \(\frac{1}{10}\). The first segment has 0 as its left end point, and the right end point corresponds to \(\frac{1}{10}\).
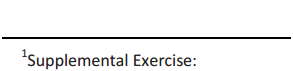
→ Have four students each stand in a square floor tile forming a straight line facing the class. Give each student a number to tie around his neck: 0, \(\frac{1}{10}\), \(\frac{2}{10}\), or \(\frac{3}{10}\). (Use index cards or construction paper.)
→ Ask a fifth student to assist by giving one end of a ball of string to the person at 0. This person holds one end of the string and passes the rest to the person to the left. (So the class sees it moving to the right.)
→ As the string gets passed down the line, each person announces her number, \(\frac{1}{10}, \frac{2}{10}, \frac{3}{10}\) stopping at \(\frac{3}{10}\).
→ The assistant cuts the string at \(\frac{3}{10}\) and gives that end of the string to the person holding , making one segment of length \(\frac{3}{10}\).
→ Have students turn over their numbers to reveal their opposites and rearrange themselves to represent the opposite of \(\frac{3}{10}\) using the same process. This time, students pass the string to the right. (So the class sees it moving to the left.)
The fraction \(\frac{a}{b}\) is located on the number line by joining a segments of length \(\frac{1}{b}\) so that (1) the left end point of the first segment is 0, and (2) the right end point of each segment is the left end point of the next segment. The right end point of the last segment corresponds to the fraction \(\frac{a}{b}\).
Answer:
→ To locate the number \(\frac{a}{b}\) on a number line, students should divide the interval between zero and 1 into b equal parts. Starting at 0, move along the number line a number of times.
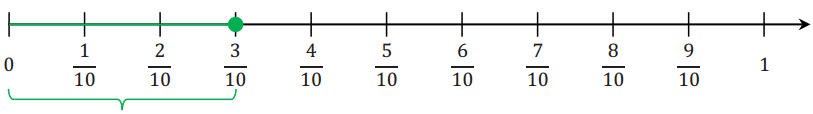
→ There are ten equal segments. Each segment has a length of \(\frac{1}{10}\). The first segment has a 0 as its left end point, and the right end point of the third segment corresponds to \(\frac{3}{10}\). The point is located at \(\frac{3}{10}\).
→ The opposite of \(\frac{3}{10}\) is located the same distance from zero as \(\frac{3}{10}\) but in the opposite direction or to the left.
Using your knowledge of opposites, what rational number represents the opposite of \(\frac{3}{10}\)?
– \(\frac{3}{10}\)
→ To locate the opposite of \(\frac{3}{10}\) on the number line, divide the interval between zero and – 1 into ten equal segments. Starting at zero, how far would we move to locate the opposite of \(\frac{3}{10}\) and in what direction?
We would move 3 units to the left of zero because that is the same distance but opposite direction we
moved to plot the point \(\frac{3}{10}\).
→ There are ten equal segments. Each segment has a length of \(\frac{1}{10}\). Three consecutive segments, starting at 0 and moving to the left, would have a total length of \(\frac{3}{10}\). The point is located at –\(\frac{3}{10}\).
\(\frac{3}{10}\)
→ Counting three consecutive segments of length of \(\frac{1}{10}\) from 0 moving to the left and taking the end point of the last segment corresponds to the number –\(\frac{3}{10}\) . Therefore, the opposite of \(\frac{3}{10}\) is –\(\frac{3}{10}\).
Locate and graph the number \(\frac{3}{10}\) and its opposite on a number line.
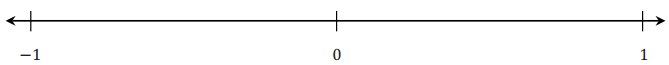
Answer:

Example 2.
Rational Numbers and the Real World
The water level of a lake rose 1.25 feet after it rained. Answer the following questions using the number line below.
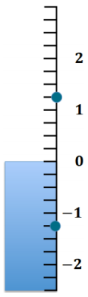
a. Write a rational number to represent the situation.
Answer:
1. 25 or 1\(\frac{1}{4}\)
b. What two integers is 1. 25 between on a number line?
Answer:
1 and 2
c. Write the length of each segment on the number line as a decimal and a fraction.
Answer:
0. 25 and \(\frac{1}{4}\)
d. What will be the water level after It rained? Graph the point on the number line.
Answer:
1.25 feet above the original lake level
e. After two weeks have passed, the water level of the lake Is now the opposite of the water level when It rained. What will be the new water level? Graph the point on the number line. Explain how you determined your answer.
Answer:
The water level would be 1.25 feet below the original lake level. If the water level was 1.25, the opposite of 1.25 is – 1.25.
f. State a rational number that is not an integer whose value is less than 1. 25, and describe Its location between two consecutive integers on the number line.
Answer:
Answers will vary. A rational number whose value is less than 1.25 is 0.75. It would be located between 0 and 1 on a number line.
Eureka Math Grade 6 Module 3 Lesson 6 Exercise Answer Key
Exercise 1.
Use what you know about the point –\(\frac{7}{4}\) and its opposite to graph both points on the number line below. The fraction – \(\frac{7}{4}\) is located between which two consecutive integers? Explain your reasoning.
![]()
Answer:

On the number line, each segment will have an equal length of \(\frac{1}{4}\). The fraction is located between – 1 and – 2.
Explanation:
\(\frac{7}{4}\) is the opposite of –\(\frac{7}{4}\). It is the same distance from zero but on the opposite side of zero. Since \(-\frac{7}{4}\) is to the left of zero, \(\frac{7}{4}\)is to the right of zero. The original fraction is located between – 2 (or –\(\frac{8}{4}\) and – 1 (or – \(\frac{4}{4}\)).
Exercise 2.
Our Story Problem
Answer:
Answers will vary.
Melissa and Samantha weigh the same amount. Melissa gained 5.5 pounds last month, while Samantha lost the same amount Melissa gained.

→ Our Scale: 1
→ Our Units: Pounds
→ Description: On the number line, zero represents Melissa and Samantha’s original weight. The point – 5.5 represents the change in Samantha’s weight. The amount lost is 5.5 pounds.
→ Other Information: A rational number to the left of 5.5 is 4. 5. A rational number to the right of 5.5 is 5.75.
Eureka Math Grade 6 Module 3 Lesson 6 Problem Set Answer Key
Question 1.
In the space provided, write the opposite of each number.
a. \(\frac{10}{7}\)
Answer:
\(-\frac{10}{7}\)
b. \(-\frac{5}{3}\)
Answer:
\(\frac{5}{3}\)
c. 3.82
Answer:
– 3. 82
d. -6\(-\frac{1}{2}\)
Answer:
6\(\frac{1}{2}\)
Question 2.
Choose a non-integer between O and 1. Label it point A and its opposite point B on the number line. Write values below the points.
Answer:
(Answers may vary)
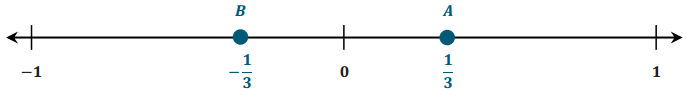
a. To draw a scale that would include both points, what could be the length of each segment?
Answer:
Answers may vary. \(\frac{1}{3}\)
b. In words, create a real-world situation that could represent the number line diagram.
Answer:
Answers may vary. Starting at home, I ran \(\frac{1}{3}\) mile. My brother ran \(\frac{1}{3}\) mile from home in the opposite direction.
Question 3.
Choose a value for point P that is between – 6 and – 7.
Answer:
Answers may vary. – \(\frac{13}{2}\), – 6.25, – 6.8
a. What is the opposite of point P?
Answer:
Answers may vary. \(\frac{13}{2}\), 6.25, 6.8
b. Use the value from part (a), and describe its location on the number line in relation to zero.
Answer:
\(\frac{13}{2}\) is the same distance as –\(\frac{13}{2}\) from zero but to the right. \(\frac{13}{2}\) is 6\(\frac{1}{2}\) units to the right of (or above) zero.
c. Find the opposite of the opposite of point P. Show your work, and explain your reasoning.
Answer:
The opposite of an opposite of the number ¡s the original number. If point P is located at – \(\frac{13}{2}\), then the
opposite of the opposite of point P is located at –\(\frac{13}{2}\) . The opposite of – \(\frac{13}{2}\) is \(\frac{13}{2}\). The opposite of \(\frac{13}{2}\) is –\(\frac{13}{2}\)
– (- \(\frac{13}{2}\)) = \(\frac{13}{2}\) and – (- (- \(\frac{13}{2}\))) = – \(\frac{13}{2}\)
Question 4.
Locate and label each point on the number line. Use the diagram to answer the questions.
Jill lives one block north of the pizza shop.
Janette’s house is \(\frac{1}{3}\) block past Jill’s house.
Jeffrey and Olivia are in the park \(\frac{4}{3}\) blocks south of the pizza shop.
Jenny’s Jazzy Jewelry Shop is located halfway between the pizza shop and the park.
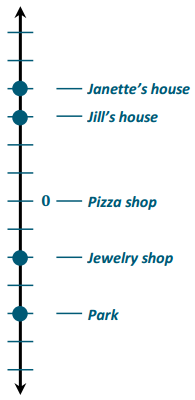
a. Describe an appropriate scale to show all the points in this situation.
Answer:
An appropriate scale would be \(\frac{1}{3}\) because the numbers given in the example all have denominators of 3. I would divide the number line into equal segments of \(\frac{1}{3}\).
b. What number represents the location of Jenny’s Jazzy Jewelry Shop? Explain your reasoning.
Answer:
The number is –\(\frac{2}{3}\). I got my answer by finding the park first. It is 4 units below 0. Since the jewelry shop is halfway between the pizza shop and the park, half of 4 is 2. Then, I moved 2 units down on the number line since the shop is south of the pizza shop before the park.
Eureka Math Grade 6 Module 3 Lesson 6 Exit Ticket Answer Key
Use the number line diagram below to answer the following questions.
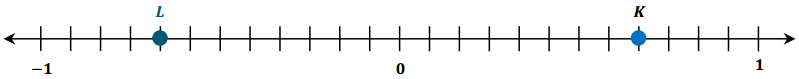
Question 1.
What is the length of each segment on the number line?
Answer:
\(\frac{1}{12}\)
Question 2.
What number does point K represent?
Answer:
\(\frac{8}{12}\) or \(\frac{2}{3}\)
Question 3.
What is the opposite of point K?
Answer:
\(-\frac{8}{12}\) or \(-\frac{2}{3}\)
Question 4.
Locate the opposite of point K on the number line, and label it point L.
Answer:
Question 5.
In the diagram above, zero represents the location of Martin Luther King Middle School. Point K represents the library, which is located to the east of the middle school. In words, create a real-world situation that could represent point L, and describe its location in relation to 0 and point K.
Answer:
Answers may vary. Point L is \(\frac{8}{12}\) units to the left of 0, so it is a negative number. Point L represents the recreation center, which is located \(\frac{8}{12}\) mile west of Martin Luther King Middle School. This means that the recreation center and library are the same distance from the middle school but in opposite directions because the opposite of \(\frac{8}{12}\) is \(-\frac{8}{12}\)
Eureka Math Grade 6 Module 3 Lesson 6 Opening Exercise Answer Key
a. Write the decimal equivalent of each fraction.
i. \(\frac{1}{2}\)
Answer:
0.5
ii. \(\frac{4}{5}\)
Answer:
0.8
iii. 6\(\frac{7}{10}\)
Answer:
6.70
b. Write the fraction equivalent of each decimal.
i. 0.42
Answer:
\(\frac{42}{100}=\frac{21}{50}\)
ii. 3.75
Answer:
\(3 \frac{75}{100}=3 \frac{3}{4}\)
iii. 36.90
Answer:
\(36 \frac{90}{100}=36 \frac{9}{10}\)