Engage NY Eureka Math Grade 6 Module 4 Lesson 34 Answer Key
Eureka Math Grade 6 Module 4 Lesson 34 Example Answer Key
Example 1:
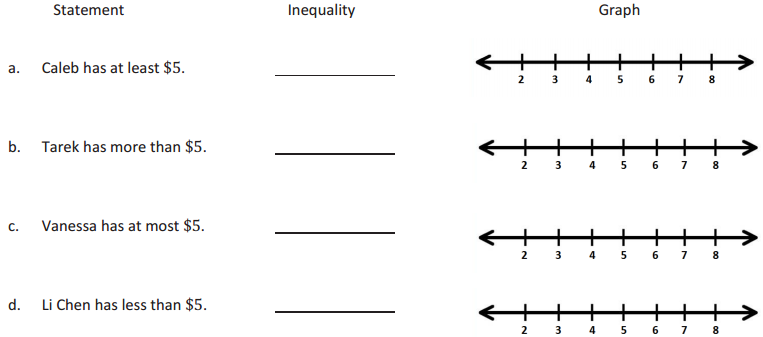
Answer:
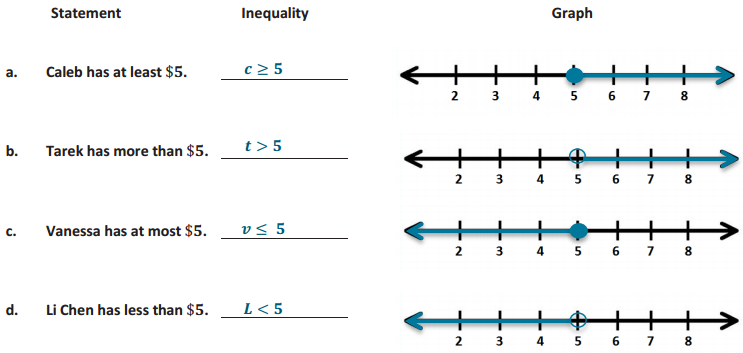
Example 2:
Kelly works for Quick Oil Change. If customers have to wait longer than 20 minutes for the oil change, the company does not charge for the service. The fastest oil change that Kelly has ever done took 6 minutes. Show the possible customer wait times in which the company charges the customer ![]()
Answer:
![]()
6 ≤ x ≤ 20
Example 3:
Gurnaz has been mowing lawns to save money for a concert. Gurnaz will need to work for at least six hours to save enough money, but he must work fewer than 16 hours this week. Write an inequality to represent this situation, and then graph the solution.
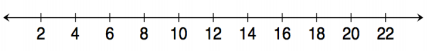
Answer:

6 ≤ x ≤ 16
Eureka Math Grade 6 Module 4 Lesson 34 Exercise Answer Key
Exercises 1 – 5:
Write an inequality to represent each situation. Then, graph the solution.
Exercise 1.
Blayton is at most 2 meters above sea level.
![]()
Answer:

b ≤ 2 where b is Blayton’s position in relationship to sea level in meters.
Exercise 2.
Edith must read for a minimum of 20 minutes.
![]()
Answer:

E ≤ 20, where E is the number of minutes Edith reads.
Exercise 3.
Travis milks his cows each morning. He has never gotten fewer than 3 gallons of milk; however, he always gets fewer than 9 gallons of milk.
![]()
Answer:

3 ≤ x < 9, where x represents the gallons of milk.
Exercise 4.
Rita can make 8 cakes for a bakery each day. So far, she has orders for more than 32 cakes. Right now, Rita needs more than four days to make all 32 cakes.

Answer:

x > 4, where x is the number of days Rito has to bake the cakes.
Exercise 5.
Rita must have all the orders placed right now done In 7 days or fewer. How will this change your inequality and your graph?

Answer:

4 < x ≤ 7
Our inequality will change because there is a range for the number of days Rita has to bake the cakes. The graph has changed because Rita is more limited in the amount of time she has to bake the cakes. Instead of the graph showing any number larger than 4, the graph now has a solid circle at 7 because Rita must be done baking the cakes in a maximum of 7 days.
Possible Extension Exercises 6 – 10:
Exercise 6.
Kasey has been mowing lawns to save up money for a concert. He earns $15 per hour and needs at least $90 to go to the concert. How many hours should he mow?
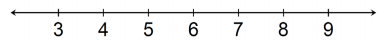
Answer:

15 x ≥ 90
\(\frac{15 x}{15} \geq \frac{90}{15}\)
x ≥ 6
kasey will need to mow for 6 or more hours.
Exercise 7.
Rachel can make 8 cakes for a bakery each day. So far, she has orders for more than 32 cakes. How many days will it take her to complete the orders?
![]()
Answer:

8x > 32
\(\frac{8 x}{8}>\frac{32}{8}\)
x > 4
Exercise 8.
Ranger saves $70 each week. He needs to save at least $2,800 to go on a trip to Europe. How many weeks will he need to save?
![]()
Answer:

70x ≥ 2800
\(\frac{70 x}{70} \geq \frac{2800}{70}\)
x ≥ 40
Exercise 9.
Clara has less than $75. She wants to buy 3 pairs of shoes. What price shoes can Clara afford if all the shoes are the same price?
![]()
Answer:

3x < 75
\(\frac{3 x}{3}<\frac{75}{3}\)
x < 25
Clara can afford shoes that are greater than $0 and less than $25.
Exercise 10.
A gym charges $25 per month plus $4 extra to swim in the pool for an hour. If a member only has $45 to spend each month, at most how many hours can the member swim?
![]()
Answer:

4x + 25 ≤ 45
4x + 25 – 25 ≤ 45 – 25
4x ≤ 20
\(\frac{4 x}{4} \leq \frac{20}{4}\)
x ≤ 5
The member can swim in the pool for 5 hours. However, we also know that the total amount of time the member spends in the pool must be greater than or equal to 0 hours because the member may choose not to swim.
0 ≤ x ≤ 5
Eureka Math Grade 6 Module 4 Lesson 34 Problem Set Answer Key
Write and graph an inequality for each problem.
Question 1.
At least 13
![]()
Answer:
![]()
x ≥ 13
Question 2.
Less than 7
![]()
Answer:
![]()
x < 7
Question 3.
Chad will need at least 24 minutes to complete the 5k race. However, he wants to finish in under 30 minutes.
![]()
Answer:

24 ≤ x < 30
Question 4.
Eva saves $60 each week. Since she needs to save at least $2,400 to go on a trip to Europe, she will need to save for at least 40 weeks.
![]()
Answer:
![]()
x ≥ 40
Question 5.
Clara has $100. She wants to buy 4 pairs of the same pants. Due to tax, Clara can afford pants that are less than $25.
![]()
Answer:
Clara must spend less than $25, but we also know that Clara will spend more than $0 when she buys pants at the store.
0 < x < 25

Question 6.
A gym charges $30 per month plus $4 extra to swim in the poo1 for an hour. Because a member has just $50 to spend at the gym each month, the member can swim at most 5 hours.
![]()
Answer:
The member can swim in the pool for 5 hours. However, we also know that the total amount of time the member spends in the pool must be greater than or equal to 0 hours because the member may choose not to swim.
0 ≤ x ≤ 5
![]()
Eureka Math Grade 6 Module 4 Lesson 34 Exit Ticket Answer Key
For each question, write an inequality. Then, graph your solution.
Question 1.
Keisha needs to make at least 28 costumes for the school play. Since she can make 4 costumes each week, Keisha plans to work on the costumes for at least 7 weeks.
![]()
Answer:
x ≥ 7
Keisha should plan to work on the costumes for 7 or more weeks.
![]()
Question 2.
If Keisha has to have the costumes complete in 10 weeks or fewer, how will our solution change?
![]()
Answer:
Keisha had 7 or more weeks in problem 1. It will still take her at least 7 weeks, but she cannot have more than 10 weeks.
7 ≤ x ≤ 10
![]()