Engage NY Eureka Math 7th Grade Module 1 Lesson 1 Answer Key
Eureka Math Grade 7 Module 1 Example Answer Key
Example 1.
How Fast Is Our Class?
Record the results from the paper-passing exercise in the table below.
| Key Terms from Grade 6 Ratios and Unit Rates
A ratio is an ordered pair of numbers which are not both zero. A ratio is denoted A : B to indicate the order of the numbers: the number is first, and the number is second. Two ratios A : B and C : D are equivalent ratios if there is a nonzero number c such that C = cA and D = cB. For example, two ratios are equivalent if they both have values that are equal. A ratio relationship between two types of quantities, such as 5 miles per 2 hours, can be described as a rate (i.e., the quantity 2.5 miles/hour). The numerical part of the rate is called the unit rate and is simply the value of the ratio, in this case 2.5. This means that in 1 hour the car travels 2.5 miles. The unit for the rate is miles/hour, read miles per hour. |
Answer:
To start this first class of the school year, conduct an exercise in how to pass out papers. The purpose of the task is not only to establish a routine at the start of the school year but also to provide a context to discuss ratio and rate.
Determine how papers will be passed out in class depending upon seating arrangement. For this task, it is best to divide the original stack so that one student (in each row or group) has a portion of the original stack. Based upon this determination, explain the system to students. A brief demonstration may help to provide a visual.
For example: If the room is arranged in rows, pass across the rows. Have students start on command and perhaps require that only the current paper-passing student may be out of his or her seat. If the room is arranged in groups or at tables, have the students pass papers to their left, on command, until everyone has a paper. Note: This procedure is highly customizable for use in any classroom structure.
Begin the task by handing a stack of papers to a starting person. Secretly start a stopwatch as the start command is given. Once every student has a paper, report the paper-passing time out loud. For example, “It took 12 seconds. Not bad, but let’s see if we can get these papers passed out in 11 seconds next time.”
Tell students to begin returning papers back in to the original stack, and then report the time upon completion.
- Excellent job. Now, pass them back out in 10 seconds. Excellent. Now, pass them back in 8 seconds. Pose the following questions to the students as a whole group, one question at a time.
- How will we measure our rate of passing out papers?
- Using a stopwatch or similar tool to measure the number of seconds taken to pass out papers.
- What quantities will we use to describe our rate?
- The number of papers passed out and the time that it took to pass them out.
Complete the second and third columns (number of papers and time) on the table as a class.
-
- Describe the quantities you want to measure by talking about what units we use to measure each quantity.
- One quantity measures the number of papers, and the other measures the number of seconds.
- Describe the quantities you want to measure by talking about what units we use to measure each quantity.
Review the Key Terms box defining ratio, rate, and unit rate in the student materials. Focus on reviewing the concept of ratio first, perhaps using a few quick examples.
Guide students to complete the ratio column in the table as shown below.
Record the results from the paper-passing exercise in the table below.
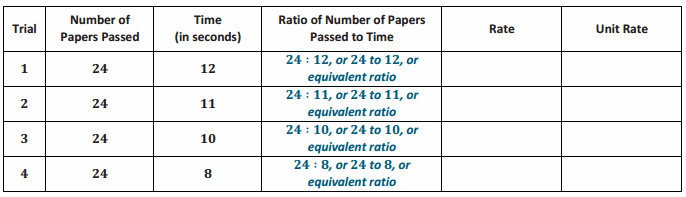
- When we started passing papers, the ratio of the number of papers to the number of seconds was 24 to 12, and by the end of the activity, the ratio of the number of papers to the number of seconds was 24 to 8.
Are these two ratios equivalent? Explain why or why not.
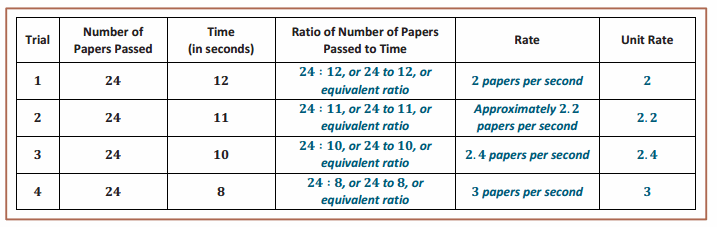
Guide students in a discussion about the fact that the number of papers was constant, and the time decreased with each successive trial. See if students can relate this to rate and ultimately determine which rate is greatest.
-
- The ratios are not equivalent since we passed the same number of papers in a shorter time. We passed 2 papers per second at the beginning and 3 papers per second by the end. Equivalent ratios must have the same value.
The following questioning is meant to guide students into the realization that unit rate helps us to make comparisons between a variety of ratios and compare different data points.
- In another class period, students were able to pass 28 papers in 15 seconds, and then 28 papers in 12 seconds. A third class period passed 18 papers in 10 seconds. How do these compare to our class?
Use sample data here, or use real data collected from other classes prepared in advance.
-
- We could find how many papers were passed per second to make these comparisons. Answers on how they compare would vary depending on class results in the table.
Review the meaning of rate and unit rate in the Key Terms box, and complete the last two columns of the table, modeling how to find both rate and unit rate. The associated unit rate is the numerical value \(\frac{A}{B}\) when there are A units of one quantity for every B units of another quantity.
Example 2:
Our Class by Gender
|
|
Number of Boys | Number of Girls | Ratio of Boys to Girls |
|
Class 1 |
|||
|
Class 2 |
|||
|
Whole 7th Grade |
Create a pair of equivalent ratios by making a comparison of quantities discussed in this Example.
Answer:
Let’s make a comparison of two quantities that are measured in the same units by comparing the ratio of the number of boys to the number of girls in this class to the ratio for different classes (and the whole grade). Sample discussion:
- In this class, we have 14 boys and 12 girls. In another class, there are 7 boys and 6 girls. Note: Any class may be used for comparison; the ratios do not need to be equivalent.
Guide students to complete the table accordingly, pausing to pose the questions below.
| Number of Boys | Number of Girls | Ratio of Boys to Girls | |
| Class 1 | 14 | 12 | 7 to 6 |
| Class 2 | 7 | 6 | 7 to 6 |
| Whole 7th Grade | Answers vary | Answers vary |
create a pair of equivalent ratios by making a comparison of quantities discussed in this example.
- Are the ratios of boys to girls in the two classes equivalent?
- What could these ratios tell us?
- What does the ratio of the number of boys to the number of girls in Class 1 to the ratio of the number of boys to the number of girls in the entire seventh-grade class tell us?
This information is necessary to have in advance.
- Are they equivalent?
- If there is a larger ratio of boys to girls in one class than in the grade as a whole, what must be true about the boy-to-girl ratio in other classes? (It may be necessary to modify this question based upon real results or provide additional examples where this is true.)
Provide ratios from four classes and the total number of students in seventh grade. Using these provided ratios, challenge students to determine the ratio of Class 5 and derive a conclusion. (See detailed explanation in chart below.)
-
- Sample solution: If the total number of students is 55 boys and 65 girls, or 120 students, then the missing number of boys for Class 5 is 55-47=8, and the missing number of girls for Class 5 is
65-49=16, resulting in a boy-to-girl ratio, 8:16=1:2, that is smaller than the whole grade ratio.
- Sample solution: If the total number of students is 55 boys and 65 girls, or 120 students, then the missing number of boys for Class 5 is 55-47=8, and the missing number of girls for Class 5 is
This extension also allows for students to see the usefulness of using the unit rate when making comparisons.
- How do we compare ratios when we have varying sizes of quantities?
- Finding the unit rate may help. In the data given here, the unit rate for both Classes 1 and 2 is approximately 1.16, and the unit rate for the whole grade is approximately 0.85. The unit rate for Class 4 is approximately 0.53, and the unit rate for Class 5 is 0.5.

The total number of students in the entire 7th grade is 120, which can be used to find the numbers for Class 5.
Review the Key Terms box focusing on the meaning of equivalent ratios, and give students 2 minutes to write down a pair of equivalent ratios comparing boys to girls or a similar comparison from their class. Discuss responses as a whole class.
Eureka Math Grade 7 Module 1 Lesson 1 Exercise Answer Key
Exercise 1:
Which is the Better Buy?
Value-Mart is advertising a Back-to-School sale on pencils. A pack of 30 sells for $7.97, whereas a 12-pack of the same brand costs $4.77. Which is the better buy? How do you know?
Answer:
The better buy is the pack of 30. The pack of 30 has a smaller unit rate, approximately 0.27, as compared to the pack of 12 with a unit price of 0.40. You would pay $0.27 per pencil in the pack of 30, whereas you would pay $0.40 per pencil in the pack of 12.
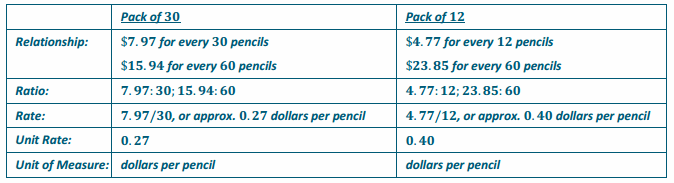
Students may instead choose to compare the costs for every 60 pencils or every 360 pencils, etc. Facilitate a discussion of the different methods students may have used to arrive at their decisions.
Eureka Math Grade 7 Module 1 Lesson 1 Problem Set Answer Key
Question 1.
Find each rate and unit rate.
a. 420 miles in 7 hours
b. 360 customers in 30 days
c. 40 meters in 16 seconds
d. $7.96 for 5 pounds
Answer:
Find each rate and unit rate.
a. 420 miles in 7 hours
Rate: 60 miles per hour; Unit Rate: 60
b. 360 customers in 30 days
Rate: 12 customers per day; Unit Rate: 12
c. 40 meters in 16 seconds
Rate: \(\frac{40}{16}\), or 2.5 meters per second; Unit Rate: 2.5
$7.96 for 5 pounds
Rate: \(\frac{7.96}{5}\), or approximately 1.59 dollars per pound; Unit Rate: 1.592
Question 2.
Write three ratios that are equivalent to the one given: The ratio of right-handed students to left-handed students is 18:4.
Answer:
Sample response: The ratio of right-handed students to left-handed students is 9:2. The ratio of right-handed students to left-handed students is 36:8. The ratio of right-handed students to left-handed students is 27:6
Question 3.
Mr. Rowley has 16 homework papers and 14 exit tickets to return. Ms. Rivera has 64 homework papers and 60 exit tickets to return. For each teacher, write a ratio to represent the number of homework papers to number of exit tickets they have to return. Are the ratios equivalent? Explain.
Answer:
Mr. Rowley’s ratio of homework papers to exit tickets is 16:14. Ms. Rivera’s ratio of homework papers to exit tickets is 64:60. The ratios are not equivalent because Mr. Rowley’s unit rate is \(\frac{8}{7}\), or approximately 1.14, and Ms. Rivera’s unit rate is \(\frac{16}{15}\), or approximately 1.07.
Question 4.
Jonathan’s parents told him that for every 5 hours of homework or reading he completes, he would be able to play 3 hours of video games. His friend Lucas’s parents told their son that he could play 30 minutes for every hour of homework or reading time he completes. If both boys spend the same amount of time on homework and reading this week, which boy gets more time playing video games? How do you know?
Answer:
If both boys spend 5 hours on homework and reading, Jonathan will be able to play 3 hours of video games, and Lucas will be able to play 2.5 hours of video games. Jonathan gets more time playing video games. Jonathan gets 0.6 hours (36 minutes) for every 1 hour of homework and reading time, whereas Lucas gets only 30 minutes for every 1 hour of homework or reading time.
Question 5.
Of the 30 girls who tried out for the lacrosse team at Euclid Middle School, 12 were selected. Of the 40 boys who tried out, 16 were selected. Are the ratios of the number of students on the team to the number of students trying out the same for both boys and girls? How do you know?
Answer:
Of the 30 girls who tried out for the lacrosse team at Euclid Middle School, 12 were selected. Of the 40 boys who tried out, 16 were selected. Are the ratios of the number of students on the team to the number of students trying out the same for both boys and girls? How do you know?
Yes, the ratios are the same: girls—12 to 30 or 2 to 5; boys—16 to 40 or 2 to 5. The value of each ratio is \(\frac{2}{5}\).
Question 6.
Devon is trying to find the unit price on a 6-pack of drinks on sale for $2.99. His sister says that at that price, each drink would cost just over $2.00. Is she correct, and how do you know? If she is not, how would Devon’s sister find the correct price?
Answer:
Devon’s sister is not correct. She divided the number of drinks by the cost, and to correctly find the unit price, she needs to divide the price by the number of drinks. \(\frac{2.99}{6}\), or approximately 0.50, is the correct unit price. The cost is approximately 0.50 dollars per drink.
Question 7.
Each year Lizzie’s school purchases student agenda books, which are sold in the school store. This year, the school purchased 350 books at a cost of $1,137.50. If the school would like to make a profit of $1,500 to help pay for field trips and school activities, what is the least amount they can charge for each agenda book? Explain how you found your answer.
Answer:
The unit price per book the school paid is 3.25. To make $1,500, you would need to make a profit of
1500÷350=4.29 per book. 3.25+4.29 is the cost per book or $7.54. $7.54∙350 generates a revenue of $2,639, and $2,639 minus the initial cost of the books, $1,137.50 (expense), gives $1,501.50 of profit.
Eureka Math Grade 7 Module 1 Lesson 1 Exit Ticket Answer Key
Students may need to see the video more than once. After watching the video the first time, it might be helpful for students to know that 100 meters is just a little longer than a football field (which measures 100 yards), and this record was recorded in 2009. Tillman the English bulldog covered a 100-meter stretch of a parking lot in a time of 19.678 seconds during the X Games XV in Los Angeles, California.
Watch the video clip of Tillman the English bulldog, the Guinness World Record holder for Fastest Dog on a Skateboard.
Question 1.
At the conclusion of the video, your classmate takes out his or her calculator and says, “Wow that was amazing! That means the dog went about 5 meters in 1 second!” Is your classmate correct, and how do you know?
Answer:
Watch the video clip of Tillman the English bulldog, the Guinness World Record holder for Fastest Dog on a Skateboard.
At the conclusion of the video, your classmate takes out his or her calculator and says, “Wow that was amazing! That means the dog went about 5 meters in 1 second!” Is your classmate correct, and how do you know?
Yes, the classmate is correct. The dog traveled at an average rate of 100 meters in 19.678 seconds, or an associated rate of \(\frac{100}{19.678}\) meters per second, giving a unit rate of approximately 5.08.
Question 2.
After seeing this video, another dog owner trained his dog, Lightning, to try to break Tillman’s skateboarding record. Lightning’s fastest recorded time was on a 75-meter stretch where it took him 15.5 seconds. Based on these data, did Lightning break Tillman’s record for fastest dog on a skateboard? Explain how you know.
Answer:
No, Lightning did not break Tillman’s record. Tillman traveled at an average rate of 5.08 meters per second (calculated from an associated rate of \(\frac{75}{15.5}\) meters per second), and Lightning traveled at an average rate of 4.84 meters per second (about \(\frac{1}{4}\) of a meter slower per second), making Tillman the faster skateboarder.