Engage NY Eureka Math 7th Grade Module 1 Lesson 14 Answer Key
Eureka Math Grade 7 Module 1 Lesson 14 Example Answer Key
Example 1.
Bargains
Peter’s Pants Palace advertises the following sale: Shirts are \(\frac{1}{2}\) off the original price; pants are \(\frac{1}{3}\) off the original price; and shoes are \(\frac{1}{4}\) off the original price.
a. If a pair of shoes costs $40, what is the sales price?
Answer:
Method 1: Tape Diagram
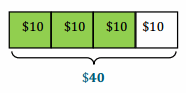
After \(\frac{1}{4}\) of the price is taken off the original price, the discounted price is $30.
Method 2:
Subtracting \(\frac{1}{4}\) of the price from the original price
40 – \(\frac{1}{4}\) (40)
40 – 10
$30
Method 3:
Finding the fractional part of the price being paid by subtracting \(\frac{1}{4}\) of the price from 1 whole
(1 – \(\frac{1}{4}\) )40
(\(\frac{3}{4}\) )40
$30
b. At Peter’s Pants Palace, a pair of pants usually sells for $33.00. What is the sales price of Peter’s pants?
Answer:
Method 1: Tape Diagram
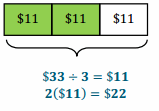
Method 2:
Use the given rate of discount, multiply by the price, and then subtract from the original price.
33 – \(\frac{1}{3}\) (33) = 33 – 11 = $22
The consumer pays \(\frac{2}{3}\) of the original price.
Method 3:
Subtract the rate from 1 whole, and then multiply that rate by the original price.
1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)
\(\frac{2}{3}\)(33) = $22.00
Use questioning to guide students to develop the methods above. Students do not need to use all three methods, but should have a working understanding of how and why they work in this problem.
Example 2.
Big Al’s Used Cars
A used car salesperson receives a commission of \(\frac{1}{12}\) of the sales price of the car for each car he sells. What would the sales commission be on a car that sold for $21,999?
Answer:
Commission = $21999(\(\frac{1}{12}\) ) = $1833.25
The sales commission would be $1,833.25 for a car sold for $21,999.
Example 3.
Tax Time
As part of a marketing plan, some businesses mark up their prices before they advertise a sales event. Some companies use this practice as a way to entice customers into the store without sacrificing their profits.
A furniture store wants to host a sales event to improve its profit margin and to reduce its tax liability before its inventory is taxed at the end of the year.
How much profit will the business make on the sale of a couch that is marked up by \(\frac{1}{3}\) and then sold at a \(\frac{1}{5}\) off discount if the original price is $2,400?
Answer:
Markup: $2400 + $2400(\(\frac{1}{3}\) ) =$3200 or $2400(1 \(\frac{1}{3}\) ) =$3200
Markdown: $3200 – $3200(\(\frac{1}{5}\) ) = $2560 or $3200(\(\frac{4}{5}\) ) =$2560
Profit = sales price – original price = $2560 – $2400 = $160.00
Example 4.
Born to Ride
A motorcycle dealer paid a certain price for a motorcycle and marked it up by \(\frac{1}{5}\) of the price he paid. Later, he sold it for $14,000. What is the original price?
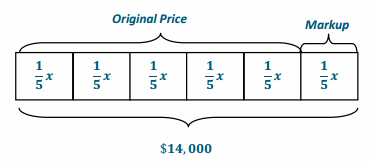
Let x = the original price
x + \(\frac{1}{5}\) x = 14000
\(\frac{6}{5}\) x=14000
(\(\frac{5}{6}\) ) \(\frac{6}{5}\) x = (\(\frac{5}{6}\) )14000
x = 11666.67
\(\frac{6}{5}\)x = 14000
(\(\frac{5}{6}\) )(\(\frac{6}{5}\) x)=(14000)(\(\frac{5}{6}\) )
x=14000(\(\frac{5}{6}\) )
x = 11666.67
The original price of the car is $11,666.67.
Eureka Math Grade 7 Module 1 Lesson 14 Problem Set Answer Key
Question 1.
A salesperson will earn a commission equal to \(\frac{1}{3}\) 2 of the total sales. What is the commission earned on sales totaling $24,000?
Answer:
(\(\frac{1}{3}\) 2)$24000=$750
Question 2.
DeMarkus says that a store overcharged him on the price of the video game he bought. He thought that the price was marked \(\frac{1}{4}\) of the original price, but it was really \(\frac{1}{4}\) off the original price. He misread the advertisement. If the original price of the game was $48, what is the difference between the price that DeMarkus thought he should pay and the price that the store charged him?
Answer:
\(\frac{1}{4}\) of $48 = $12 (the price DeMarkus thought he should pay); \(\frac{1}{4}\) off $48 = $36; Difference between prices:
$36 – $12=$24
Question 3.
What is the cost of a $1,200 washing machine after a discount of \(\frac{1}{5}\) the original price?
Answer:
(1 – \(\frac{1}{5}\) )$1200=$960 or $1200 – \(\frac{1}{5}\) ($1200)=$960
Question 4.
If a store advertised a sale that gave customers a \(\frac{1}{4}\) discount, what is the fractional part of the original price that the customer will pay?
Answer:
1 – \(\frac{1}{4}\) = \(\frac{3}{4}\) of original price
Question 5.
Mark bought an electronic tablet on sale for \(\frac{1}{4}\) off the original price of $825.00. He also wanted to use a coupon for \(\frac{1}{5}\) off the sales price. How much did Mark pay for the tablet?
Answer:
$825 (\(\frac{3}{4}\) ) =$618.75, then $618.75 (\(\frac{4}{5}\) ) =$495
Question 6.
A car dealer paid a certain price for a car and marked it up by \(\frac{7}{5}\) of the price he paid. Later, he sold it for $24,000. What is the original price?
Answer:
x + \(\frac{7}{5}\) x=24000
\(\frac{12}{5}\) x=24000
x = 10000
The original price was $10,000.
Question 7.
Joanna ran a mile in physical education class. After resting for one hour, her heart rate was 60 beats per minute. If her heart rate decreased by \(\frac{2}{5}\), what was her heart rate immediately after she ran the mile?
Answer:
x – \(\frac{2}{5}\)x = 60
\(\frac{3}{5}\) x=60
x = 100
Her heart rate was 100 beats per minute.
Eureka Math Grade 7 Module 1 Lesson 14 Exit Ticket Answer Key
Question 1.
A bicycle shop advertised all mountain bikes priced at a \(\frac{1}{3}\) discount.
a. What is the amount of the discount if the bicycle originally costs $327?
Answer:
\(\frac{1}{3}\) ($327)=$109 discount
b. What is the discount price of the bicycle?
Answer:
\(\frac{2}{3}\) ($327)=$218 discount price. Methods will vary.
c. Explain how you found your solution to part (b).
Answer:
Answers will vary.
Question 2.
A hand-held digital music player was marked down by \(\frac{1}{4}\) of the original price.
a. If the sales price is $128.00, what is the original price?
Answer:
x-\(\frac{1}{4}\) x=128
\(\frac{3}{4}\) x=128
x = 170.67
The original price is $170.67.
b. If the item was marked up by \(\frac{1}{2}\) before it was placed on the sales floor, what was the price that the store paid for the digital player?
Answer:
x + \(\frac{1}{2}\)x = 170.67
\(\frac{3}{2}\) x = 170.67
x = 113.78
The price that the store paid for the digital player was $113.78.
c. What is the difference between the discount price and the price that the store paid for the digital player?
Answer:
$128 – $113.78 = $14.22