Engage NY Eureka Math 7th Grade Module 2 Lesson 16 Answer Key
Eureka Math Grade 7 Module 2 Lesson 16 Example Answer Key
Example 1.
Using the Commutative and Associative Properties to Efficiently Multiply Rational Numbers
a. Evaluate the expression below.
-6 × 2 × (-2) × (-5) × (-3)
Answer:
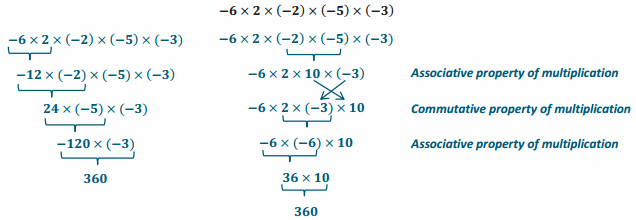
b. What types of strategies were used to evaluate the expressions?
Answer:
The strategies used were order of operations, rearranging the terms using the commutative property, and multiplying the terms in various orders using the associative property.
c. Can you identify the benefits of choosing one strategy versus another?
Answer:
Multiplying the terms allowed me to combine factors in more manageable ways, such as multiplying
(-2) × (-5) to get 10. Multiplying other numbers by 10 is very easy.
d. What is the sign of the product, and how was the sign determined?
Answer:
The product is a positive value. When calculating the product of the first two factors, the answer will be negative because when the factors have opposite signs, the result is a negative product. Two negative values multiplied together yield a positive product. When a negative value is multiplied by a positive product, the sign of the product again changes to a negative value. When this negative product is multiplied by the last (fourth) negative value, the sign of the product again changes to a positive value.
Example 2.
Using the Distributive Property to Multiply Rational Numbers
Rewrite the mixed number as a sum; then, multiply using the distributive property.
-6 × (5 \(\frac{1}{3}\))
Answer:
-6 × (5+\(\frac{1}{3}\))
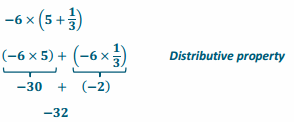
→ Did the distributive property make this problem easier to evaluate? How so?
→ Answers will vary, but most students will think that distributive property did make the problem easier to solve.
Example 3.
Using the Distributive Property to Multiply Rational Numbers
Evaluate using the distributive property.
16 × (-\(\frac{3}{8}\)) + 16 × \(\frac{1}{4}\)
16(-\(\frac{3}{8}\) + \(\frac{1}{4}\)) Distributive property
16(-\(\frac{3}{8}\) + \(\frac{2}{8}\)) Equivalent fractions
16(-\(\frac{1}{8}\))
-2
Example 4.
Using the Multiplicative Inverse to Rewrite Division as Multiplication
Rewrite the expression as only multiplication and evaluate.
1 ÷ \(\frac{2}{3}\) × (-8) × 3 ÷ (-\(\frac{1}{2}\))
Answer:
1 ÷ \(\frac{2}{3}\) × (-8) × 3 ÷ (-\(\frac{1}{2}\))

Eureka Math Grade 7 Module 2 Lesson 16 Exercise Answer Key
Exercise 1.
Find an efficient strategy to evaluate the expression and complete the necessary work.
-1 × (-3) × 10 × (-2) × 2
Answer:
Methods will vary.
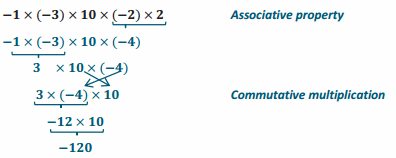
Exercise 2.
Find an efficient strategy to evaluate the expression and complete the necessary work.
Methods will vary.
4 × \(\frac{1}{3}\) × (-8) × 9 × (-\(\frac{1}{2}\))
Answer:

Exercise 3.
What terms did you combine first and why?
Answer:
I multiplied the –\(\frac{1}{2}\) × -8 and \(\frac{1}{3}\) × 9 because their products are integers; this eliminated the fractions.
Exercise 4.
Refer to the example and exercises. Do you see an easy way to determine the sign of the product first?
Answer:
The product of two negative integers yields a positive product. If there is an even number of negative factors, then each negative value can be paired with another negative value yielding a positive product. This means that all factors become positive values and, therefore, have a positive product.
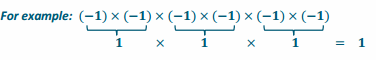
If there are an odd number of negative factors, then all except one can be paired with another negative. This leaves us with a product of a positive value and a negative value, which is negative.
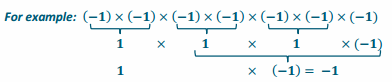
Exercise 5.
Multiply the expression using the distributive property.
9 × (-3 \(\frac{1}{2}\))
Answer:
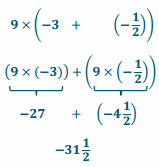
Exercise 6.
4.2 × (-\(\frac{1}{3}\))÷\(\frac{1}{6}\) × (-10)
Answer:
4.2 × (-\(\frac{1}{3}\))÷\(\frac{1}{6}\) × (-10)

Eureka Math Grade 7 Module 2 Lesson 16 Problem Set Answer Key
Question 1.
Evaluate the expression -2.2 × (-2)÷(-\(\frac{1}{4}\)) × 5
a. Using the order of operations only.
Answer:
4.4 ÷ (-\(\frac{1}{4}\)) × 5
-17.6 × 5
-88
b. Using the properties and methods used in Lesson 16.
Answer:
-2.2 × (-2) × (-4) × 5
-2.2 × (-2) × 5 × (-4)
-2.2 × (-10) × (-4)
22 × (-4)
-88
c. If you were asked to evaluate another expression, which method would you use, (a) or (b), and why?
Answer:
Answers will vary; however, most students should have found method (b) to be more efficient.
Question 2.
Evaluate the expressions using the distributive property.
a. (2 \(\frac{1}{4}\)) × (-8)
Answer:
2 × (-8)+\(\frac{1}{4}\) × (-8)
-16 + (-2)
-18
b. \(\frac{2}{3}\)(-7)+\(\frac{2}{3}\)(-5)
Answer:
\(\frac{2}{3}\) (-7+(-5))
\(\frac{2}{3}\) (-12)
-8
Question 3.
Mia evaluated the expression below but got an incorrect answer. Find Mia’s error(s), find the correct value of the expression, and explain how Mia could have avoided her error(s).
0.38 × 3÷(-\(\frac{1}{2}\)0) × 5÷(-8)
0.38 × 5 × (\(\frac{1}{2}\)0) × 3 × (-8)
0.38 × (\(\frac{1}{4}\)) × 3 × (-8)
0.38 × (\(\frac{1}{4}\)) × (-24)
0.38 × (-6)
-2.28
Answer:
Mia made two mistakes in the second line; first, she dropped the negative symbol from –\(\frac{1}{20}\) when she changed division to multiplication. The correct term should be (-20) because dividing a number is equivalent to multiplying its multiplicative inverse (or reciprocal). Mia’s second error occurred when she changed division to multiplication at the end of the expression; she changed only the operation, not the number. The term should be (-\(\frac{1}{8}\)). The correct value of the expressions is 14 \(\frac{1}{4}\), or 14.25.
Mia could have avoided part of her error if she had determined the sign of the product first. There are two negative values being multiplied, so her answer should have been a positive value.
Eureka Math Grade 7 Module 2 Lesson 15 Integer Multiplication Round 1 Answer Key
Directions: Determine the quotient of the integers, and write it in the column to the right.
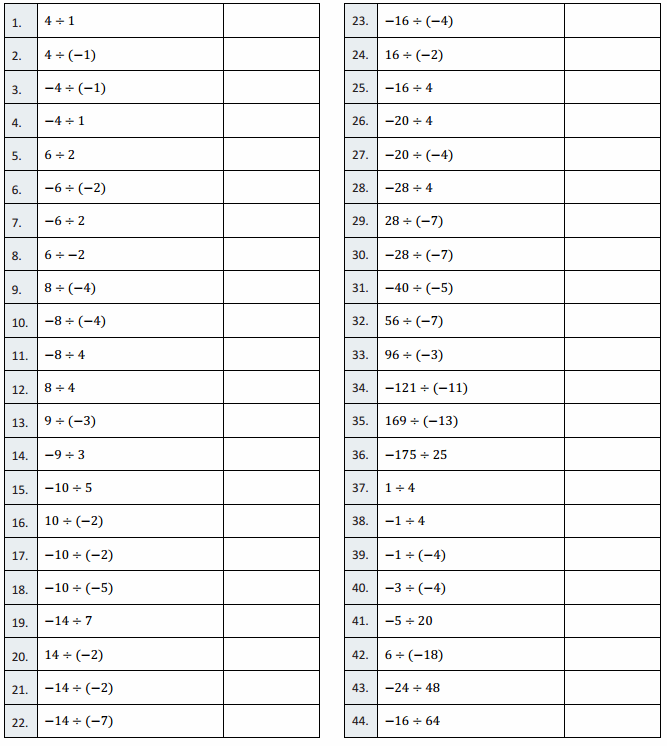
Answer:
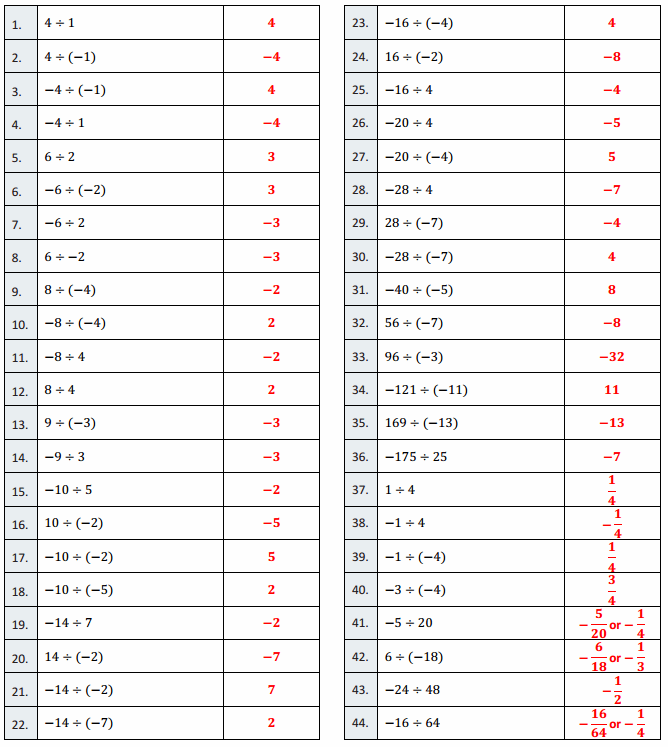
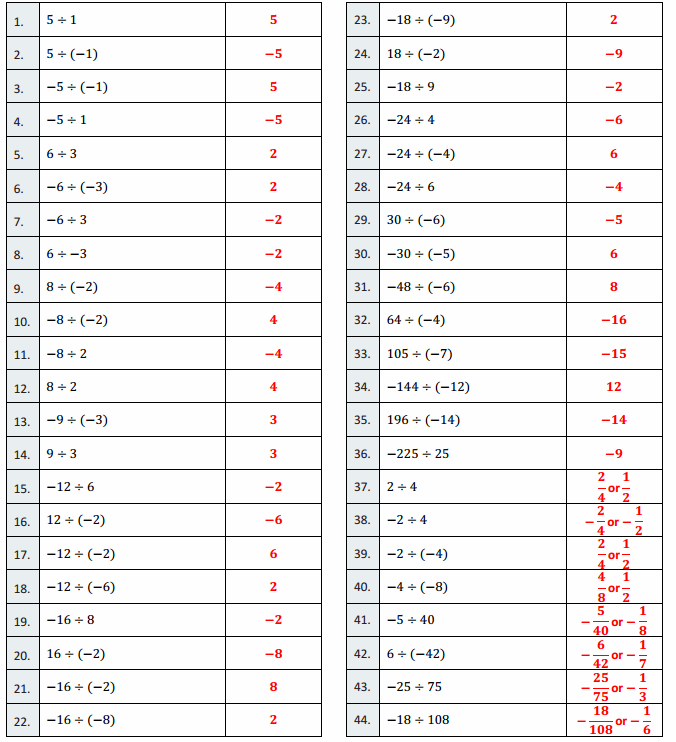
Eureka Math Grade 7 Module 2 Lesson 15 Integer Multiplication Round 2 Answer Key
Answer:
Eureka Math Grade 7 Module 2 Lesson 16 Exit Ticket Answer Key
Question 1.
Evaluate the expression below using the properties of operations.
18÷(-\(\frac{2}{3}\)) × 4÷(-7) × (-3)÷(\(\frac{1}{4}\))
Answer:
18 × (-\(\frac{3}{2}\)) × 4 × (-\(\frac{1}{7}\)) × (-3) × (\(\frac{4}{1}\))
-27 × 4 × (-\(\frac{1}{7}\)) × (-3) × (\(\frac{4}{1}\))
–\(\frac{1296}{7}\)
Answer: -185 \(\frac{1}{7}\) or –\(-185 . \overline{142857}\)
Question 2.
a. Given the expression below, what will the sign of the product be? Justify your answer.
-4 × (-\(\frac{8}{9}\)) × 2.78 × (1 \(\frac{1}{3}\)) × (-\(\frac{2}{5}\)) × (-6.2) × (-0.2873) × (3\(\frac{1}{11}\)) × A
Answer:
There are five negative values in the expression. Because the product of two numbers with the same sign yield a positive product, pairs of negative factors have positive products. Given an odd number of negative factors, all but one can be paired into positive products. The remaining negative factor causes the product of the terms without A to be a negative value. If the value of A is negative, then the pair of negative factors forms a positive product. If the value of A is positive, the product of the two factors with opposite signs yields a negative product.
b. Give a value for A that would result in a positive value for the expression.
Answer:
Answers will vary, but the answer must be negative. -2
c. Give a value for A that would result in a negative value for the expression.
Answer:
Answers will vary, but the answer must be positive. 3.6