Engage NY Eureka Math 7th Grade Module 2 Lesson 17 Answer Key
Eureka Math Grade 7 Module 2 Lesson 17 Opening Exercise Answer Key
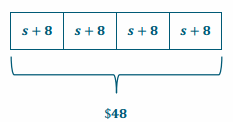
For his birthday, Zack and three of his friends went to a movie. They each got a ticket for $8.00 and the same snack from the concession stand. If Zack’s mom paid $48 for the group’s tickets and snacks, how much did each snack cost?
The equation 4(s+8)=48 represents the situation when s represents the cost, in dollars, of one snack.
Answer:
4(s + 8) = 48
\(\frac{1}{4}\) (4(s+8))=\(\frac{1}{4}\) (48)
s + 8 = 12
s + 8 – 8 = 12 – 8
s+0=4
s=4
OR
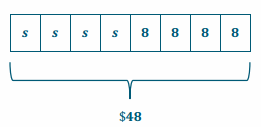
4(s+8)=48
4s+32=48
4s+32-32=48-32
4s+0=16
4s=16
\(\frac{1}{4}\) (4s)=\(\frac{1}{4}\) (16)
1s=4
s=4
Eureka Math Grade 7 Module 2 Lesson 17 Exercise Answer Key
Exercise
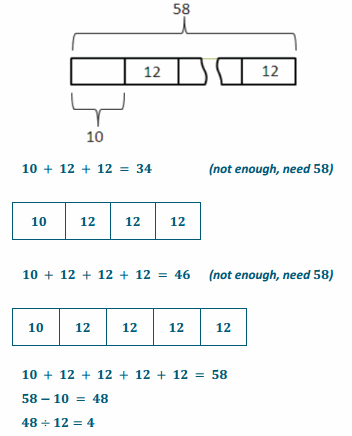
The cost of a babysitting service on a cruise is $10 for the first hour and $12 for each additional hour. If the total cost of babysitting baby Aaron was $58, how many hours was Aaron at the sitter?
Algebraic Solution
h = number of additional hours
12h + 10 = 58
12h + 10-10 = 58-10
12h + 0 = 48
(\(\frac{1}{12}\) )(12h)=(48)(\(\frac{1}{12}\) )
1h = 4
h=4
1+4=5
Aaron was with the babysitter for 5 hours
Eureka Math Grade 7 Module 2 Lesson 17 Exploratory Challenge Answer Key
Exploratory Challenge: Expenses on Your Family Vacation
John and Ag are summarizing some of the expenses of their family vacation for themselves and their three children, Louie, Missy, and Bonnie. Write an algebraic equation, create a model to determine how much each item will cost using all of the given information, and answer the questions that follow.
Expenses:

Your Group’s Scenario Solution:
Answer:
Scenario 1
During one rainy day on the vacation, the entire family decided to go watch a matinee movie in the morning and a drive-in movie in the evening. The price for a matinee movie in the morning is different than the cost of a drive-in movie in the evening. The tickets for the matinee morning movie cost $6 each. How much did each person spend that day on movie tickets if the ticket cost for each family member was the same? What was the cost for a ticket for the drive-in movie in the evening?
Answer:
Algebraic Equation & Solution
Morning matinee movie: $6 each
Evening drive-in movie: e each
5(e+6)=75
5e+30=75
5e+30-30=75-30
5e+0=45
(\(\frac{1}{5}\))5e=45(\(\frac{1}{5}\))
1e=9
e=9
OR
5(e+6)=75
(\(\frac{1}{5}\) )5(e+6)=75(\(\frac{1}{5}\) )
e+6=15
e+6-6=15-6
e =9
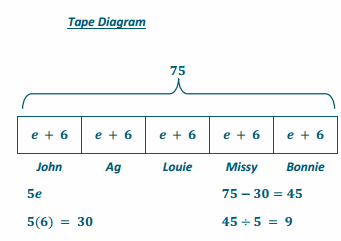
The total each person spent on movies in one day was $15. The evening drive-in movie costs $9 each
Scenario 2
For dinner one night, the family went to the local pizza parlor. The cost of a soda was $3. If each member of the family had a soda and one slice of pizza, how much did one slice of pizza cost?
Answer:
Algebraic Equation & Solution
One Soda: $3
Slice of Pizza: p dollars
5(p+3)=37.95
5p +15 = 37.95
5p+15-15 =37.95 -15
5p+0=22.95
(\(\frac{1}{5}\) )5p=22.95(\(\frac{1}{5}\) )
1p = 4.59
p= 4.59
OR
5(p+3)=37.95
(\(\frac{1}{5}\) )5(p+3)=(37.95)(\(\frac{1}{5}\) )
p + 3 = 7.59
p + 3-3 = 7.59-3
p = 4.59
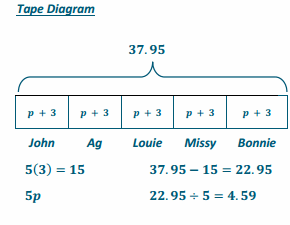
one slice of pizza cost $4.59
Scenario 3
One night, John, Louie, and Bonnie went to see the local baseball team play a game. They each bought a game ticket and a hat that cost $10. How much was each ticket to enter the ballpark?
Answer:
Algebraic Equation & Solution
Ticket: t dollars
Hat: $10
3(t +10)=103.83
3t + 30 = 103.83
3t+30-30=103.83-30
3t + 0 = 73.83
(\(\frac{1}{3}\) )3t=73.83(\(\frac{1}{3}\) )
1t = 24.61
t = 24.61
OR
3(t +10)=103.83
(\(\frac{1}{3}\) )3(t +10)=(103.83)(\(\frac{1}{3}\) )
t+10=34.61
t+10-10=34.61-10
t=24.61
One ticket costs $24.61.
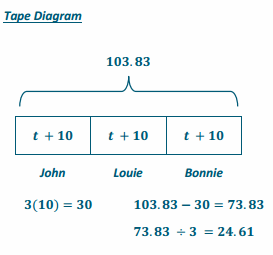
Scenario 4.
While John, Louie, and Bonnie went to see the baseball game, Ag and Missy went shopping. They bought a T-shirt for each member of the family and bought two pairs of sandals that cost $10 a pair. How much was each T-shirt?
Answer:
Algebraic Equation & Solution
T-Shirt: t dollars
Sandals: 2 × $10 = $20
5t + 20 = 120
5t +20-20 =120- 20
5t + 0 = 100
(\(\frac{1}{5}\) )5t=100(\(\frac{1}{5}\) )
1t=20
t=20
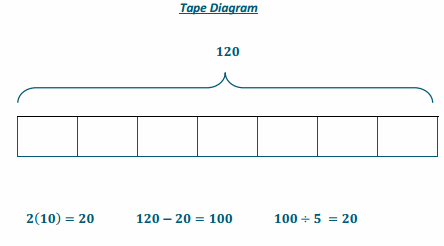
One T-shirt costs $20.
Scenario 5.
The family flew in an airplane to their vacation destination. Each person had to have his own ticket for the plane and also pay $25 in insurance fees per person. What was the cost of one ticket?
Answer:
Algebraic Equation & Solution
One ticket: t dollars
Insurance: $25 per person
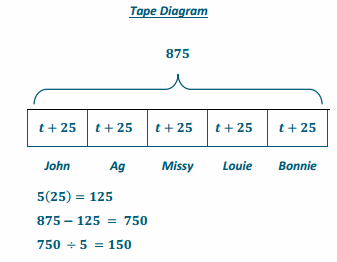
5(t + 25) =875
5t +125-125=875 -125
5t + 0 = 750
5t=750(\(\frac{1}{5}\) )
t = 150
OR
5(t + 25)=875
(\(\frac{1}{5}\) )5(t+25)=(\(\frac{1}{5}\) )(875)
t+25=175
t+25-25=175-25
t = 150
One ticket costs $150.
Scenario 6
While on vacation, the family rented a car to get them to all the places they wanted to see for five days. The car costs a certain amount each day, plus a one-time insurance fee of $50. How much was the daily cost of the car (not including the insurance fees)?
Answer:
Algebraic Equation & Solution
Daily fee: d dollars
Insurance fee: $50
5d + 50 = 400
5d +50-50 =400 –50
5d+0=350
(\(\frac{1}{5}\) )5d=350(\(\frac{1}{5}\) )
1d = 70
d = 70
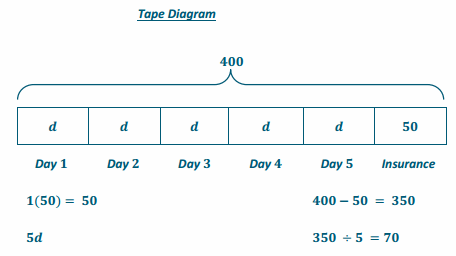
one day costs $70
Scenario 7.
The family decided to stay in a motel for four nights. The motel charges a nightly fee plus $60 in state taxes. What is the nightly charge with no taxes included?
Answer:
Algebraic Equation & Solution
Nightly charge: n dollars
Taxes: $60
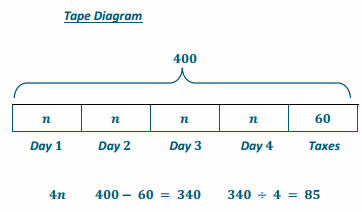
4n + 60 = 400
4n +60-60 =400-60
4n + 0=340
(\(\frac{1}{4}\) )4n=340(\(\frac{1}{4}\) )
1n = 85
n = 85
One night costs $85.
After collaborating with all of the groups, summarize the findings in the table below.
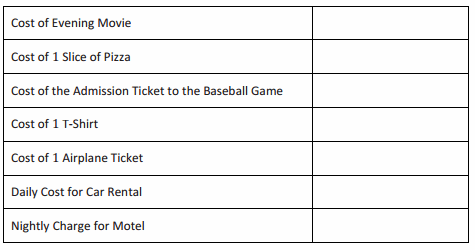
Answer:
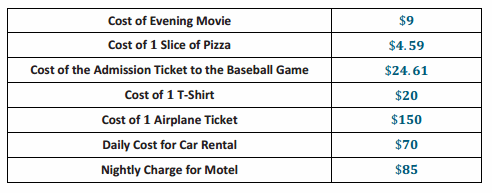
Using the results, determine the cost of the following:
Question 1.
A slice of pizza, 1 plane ticket, 2 nights in the motel, and 1 evening movie.
Answer:
4.59 + 150 + 2(85) + 9 = 333.59
Question 2.
One T-shirt, 1 ticket to the baseball game, and 1 day of the rental car.
Answer:
20 + 24.61 + 70 = 114.61
Eureka Math Grade 7 Module 2 Lesson 17 Problem Set Answer Key
Question 1.
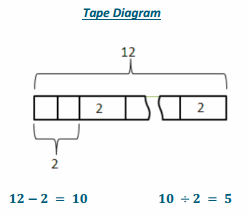
A taxi cab in Myrtle Beach charges $2 per mile and $1 for every person. If a taxi cab ride for two people costs $12, how far did the taxi cab travel?
Answer:
Algebraic Equation & Solution
Number of miles: m
People: 2
12-2 = 10 10 ÷2 = 5
2m+2=12
2m+2-2=12-2
2m+0=10
(1/2)2m=10(1/2)
1m=5
m = 5
The taxi cab traveled 5 miles.
Question 2.
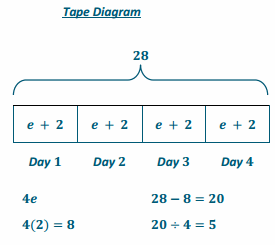
Heather works as a waitress at her family’s restaurant. She works 2 hours every morning during the breakfast shift and returns to work each evening for the dinner shift. In the last four days, she worked 28 hours. If Heather works the same number of hours every evening, how many hours did she work during each dinner shift?
Answer:
Algebraic Equation & Solution
Number of morning hours: 2
Number of evening hours: e
4(e +2)=28
4e+8-8=28-8
4e+0=20
(\(\frac{1}{4}\) )4e=20(\(\frac{1}{4}\) )
1e=5
e=5
OR
(\(\frac{1}{4}\) )4(e+2)=28(\(\frac{1}{4}\) )
e+2=7
e+2-2=7-2
e=5
Heather worked 5 hours in the evening.
Question 3.
Jillian exercises 5 times a week. She runs 3 miles each morning and bikes in the evening. If she exercises a total of 30 miles for the week, how many miles does she bike each evening?
Answer:
Algebraic Equation & Solution
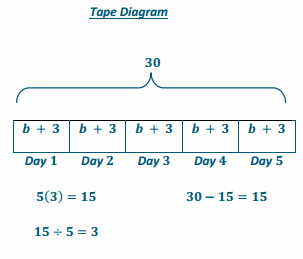
Run: 3 mi.
Bikes: b mi.
OR
(\(\frac{1}{5}\) )(b+3)=30(\(\frac{1}{5}\) )
b+3=6
b+3-3=6-3
b=3
Jillian bikes 3 miles every evening.
Question 4.
Marc eats an egg sandwich for breakfast and a big burger for lunch every day. The egg sandwich has 250 calories. If Marc has 5,250 calories for breakfast and lunch for the week in total, how many calories are in one big burger?
Answer:
Algebraic Equation & Solution
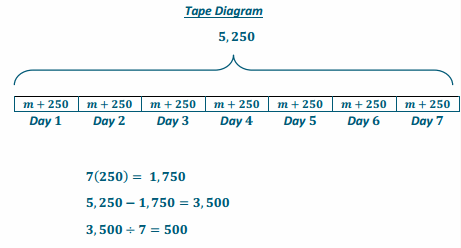
Egg Sandwich: 250 cal.
Hamburger: m cal
7(m+250)=5,250
7m+1,750-1750=5250-1750
7m+0=3,500
(\(\frac{1}{7}\) )7m=3,500(\(\frac{1}{7}\) )
1m = 500
m=500
OR
(\(\frac{1}{7}\) )7(m+250)=(\(\frac{1}{7}\) )5,250
m+250=750
m+250-250=750-250
m=500
Each hamburger has 500 calories.
Question 5.
Jackie won tickets playing the bowling game at the local arcade. The first time, she won 60 tickets. The second time, she won a bonus, which was 4 times the number of tickets of the original second prize. Altogether she won 200 tickets. How many tickets was the original second prize?
Answer:
Algebraic Equation & Solution
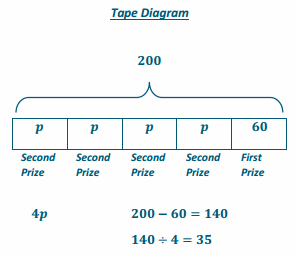
First Prize: 60 tickets
Second Prize: p tickets
4p+60=200
4p+60-60=200-60
4p+0=140
(\(\frac{1}{4}\) )4p=140(\(\frac{1}{4}\) )
1p=35
p=35
The original second prize was 35 tickets.
Eureka Math Grade 7 Module 2 Lesson 17 Exit Ticket Answer Key
Question 1.
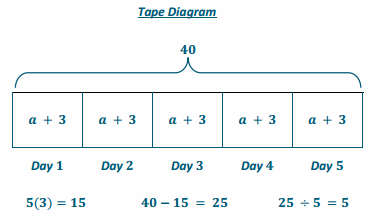
Eric’s father works two part-time jobs, one in the morning and one in the afternoon, and works a total of 40 hours each 5-day workweek. If his schedule is the same each day, and he works 3 hours each morning, how many hours does Eric’s father work each afternoon?
Answer:
Algebraic Equation & Solution
Number of afternoon hours: a
Number of morning hours: 3
5(a+3)=40
5a+15-15=40-15
5a+0= 25
(\(\frac{1}{5}\) )5a=25(\(\frac{1}{5}\) )
a=5
OR
5(a+3)=40
(\(\frac{1}{5}\) )5(a+3)=40(\(\frac{1}{5}\) )
a+3=8
a+3-3=8-3
a=5
Eric’s father works 5 hours in the afternoon.
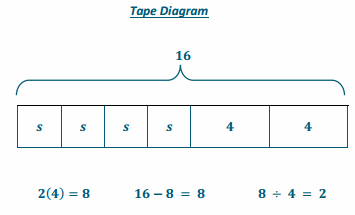
Question 2.
Henry is using a total of 16 ft. of lumber to make a bookcase. The left and right sides of the bookcase are each 4 ft. high. The top, bottom, and two shelves are all the same length, labeled S. How long is each shelf?
Answer:
Algebraic Equation & Solution
Shelves: s ft.
Sides: 8 ft.
4s+8=16
4s+8-8=16-8
4s+0=8
(\(\frac{1}{4}\) )4s=8(\(\frac{1}{4}\) )
1s=2
s=2
Each shelf is 2 ft. long.