Engage NY Eureka Math 7th Grade Module 2 Lesson 19 Answer Key
Eureka Math Grade 7 Module 2 Lesson 19 Example Answer Key
Example 1.
Tic-Tac-Toe Review
Fill in the 9 spaces with one expression from the list below. Use one expression per space. You will use 9 of the expressions:
12-4x
8x+4-12x
8(\(\frac{1}{2}\) x -2)
12-6x+2x
-4x+4
x-2+2x-4
4x-12
4(x-4)
3(x-2)
0.1(40x)-\(\frac{1}{2}\) (24)
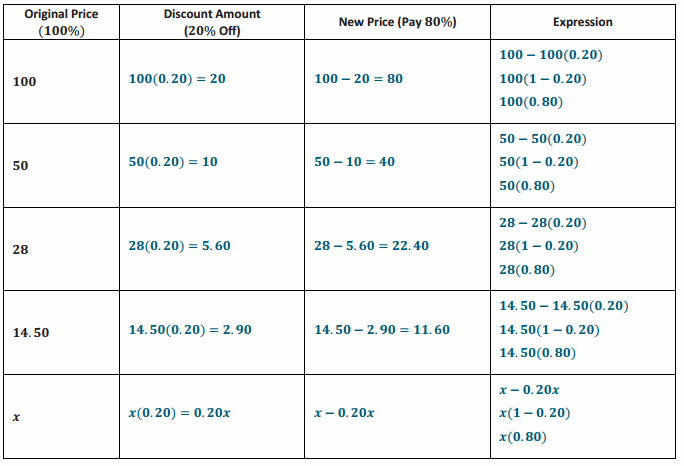
Example 2.

Answer:
Example 3.
An item that has an original price of x dollars is discounted 33%.
a. Write an expression that represents the amount of the discount.
Answer:
0.33x
b. Write two equivalent expressions that represent the new, discounted price.
Answer:
x-0 .33x
x(1-0.33)
x(0.67)
c. Use one of your expressions to calculate the new, discounted price if the original price was $56.
Answer:
0.67x
0.67(56)
37.52
The new discounted price is $37.52.
d. How would the expressions you created in parts (a) and (b) have to change if the item’s price had increased by 33% instead of decreased by 33%?
Answer:
Instead of subtracting 0.33x, you would have to add for the increase. The expression would be
x+0.33x
1.33x.
Example 4.
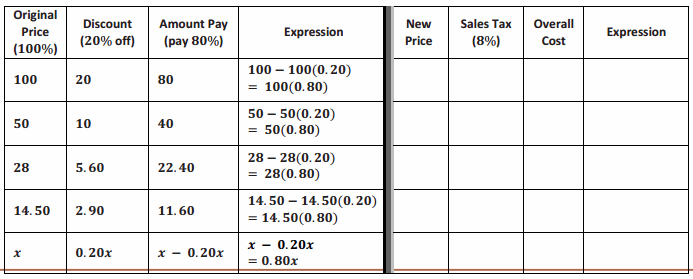
Answer:
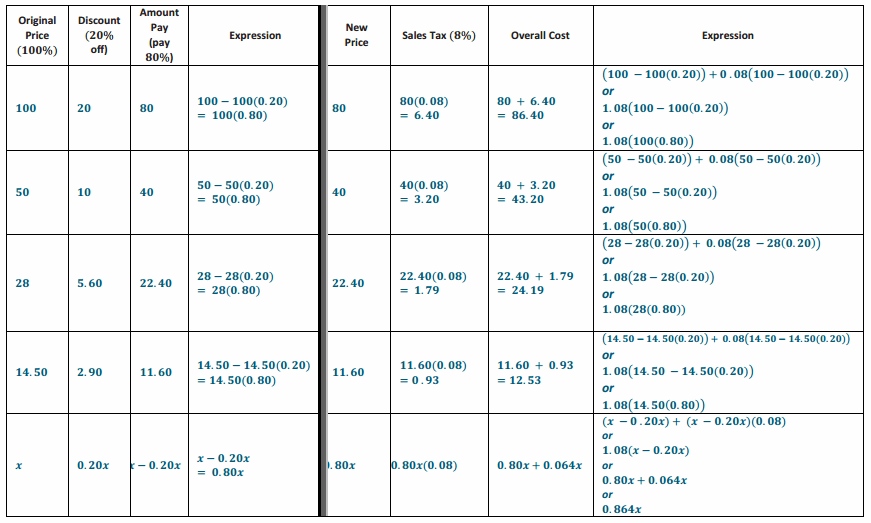
Eureka Math Grade 7 Module 2 Lesson 19 Problem Set Answer Key
Solve the following problems. If necessary, round to the nearest penny.
Question 1.
A family of 12 went to the local Italian restaurant for dinner. Every family member ordered a drink and meal, 3 ordered an appetizer, and 6 people ordered cake for dessert.
a. Write an expression that can be used to figure out the cost of the bill. Include the definitions for the variables the server used.
Answer:
d= drink
m = meal
a = appetizer
c = cake
12d+12m+3a+6c
b. The waitress wrote on her ordering pad the following expression: 3(4d+4m+a+2c). Was she correct? Explain why or why not.
Answer:
Yes, she was correct because her expression is equivalent to the expression from part (a). If the distributive property is applied, the expressions would be exact.
c. What is the cost of the bill if a drink costs $3, a meal costs $20, an appetizer costs $5.50, and a slice of cake costs $3.75?
Answer:
12d+12m+3a+6c
12(3)+12(20)+3(5.50)+6(3.75)
36+240+16.50+22.50
315
The cost of the bill is $315.
d. Suppose the family had a 10% discount coupon for the entire check and then left an 18% tip. What is the total?
Answer:
(315-315(0.10))+0.18(315-315(0.10))
1.18(315-315(0.10))
1.18(315(0.90))
334.53
After the discount and tip, the new total is $334.53.
Question 2.
Sally designs web pages for customers. She charges $135.50 per web page; however, she must pay a monthly rental fee of $650 for her office. Write an expression to determine her take-home pay after expenses. If Sally designed 5 web pages last month, what was her take-home pay after expenses?
w= number of webpages Sally designs
135.50w-650
135.50(5)-650
27.50
After expenses, Sally’s take-home pay is $27.50.
Question 3.
While shopping, Megan and her friend Rylie find a pair of boots on sale for 25% off the original price. Megan calculates the final cost of the boots by first deducting the 25% and then adding the 6% sales tax. Rylie thinks Megan will pay less if she pays the 6% sales tax first and then takes the 25% discount.
a. Write an expression to represent each girl’s scenario if the original price of the boots was x dollars.
Answer:

b. Evaluate each expression if the boots originally cost $200.
Answer:

Using both Megan’s and Rylie’s methods would show that the boots would cost $159.
c. Who was right? Explain how you know.
Answer:
Neither girl was right. They both pay the same amount.
d. Explain how both girls’ expressions are equivalent.
Answer:
Two expressions are equivalent if they yield the same number for every substitution of numbers for the variables in each expression. Since multiplication is commutative, the order of the multiplication can be reversed, and the result will remain the same.
Eureka Math Grade 7 Module 2 Lesson 19 Exit Ticket Answer Key
Question 1.
Write three equivalent expressions that can be used to find the final price of an item costing g dollars that is on sale for 15% off and charged 7% sales tax.
Answer:
(x-0.15x) + 0.07(x-0.15x) 1.07(x -0 .15x) 1.07(0.85x) or 0.85(1.07)x
Question 2.
Using all of the expressions, determine the final price for an item that costs $75. If necessary, round to the nearest penny.
Answer:
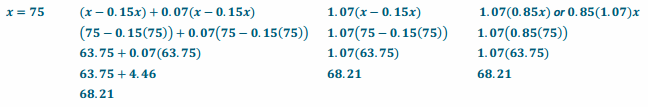
The final price of an item that costs $75 is $68.21.
Question 3.
If each expression yields the same final sale price, is there anything to be gained by using one over the other?
Answer:
Using the final two expressions makes the problem shorter and offers fewer areas to make errors. However, all three expressions are correct.
Question 4.
Describe the benefits, special characteristics, and properties of each expression.
Answer:
The second and third expressions collect like terms. The third expression can be written either way using the commutative property of multiplication. The first and second expressions find the discount price first, whereas the third expression is written in terms of percent paid.