Engage NY Eureka Math 7th Grade Module 2 Lesson 23 Answer Key
Eureka Math Grade 7 Module 2 Lesson 23 Exercise Answer Key
Exercises
Youth Group Trip
Exercise 1.
The youth group is going on a trip to an amusement park in another part of the state. The trip costs each group member $150, which includes $85 for the hotel and two one – day combination entrance and meal plan passes.
a. Write an equation representing the cost of the trip. Let P be the cost of the park pass.
Answer:
85 + 2P = 150
b. Solve the equation algebraically to find the cost of the park pass. Then write the reason that justifies each step using if – then statements.
Answer:
If: 85 + 2P = 150,
Then: 85 – 85 + 2P = 150 – 85 Subtraction property of equality for the additive inverse of 85
If: 0 + 2P = 65
Then: 2P = 65 Additive identity
If: 2P = 65
Then: (\(\frac{1}{2}\))2P = (\(\frac{1}{2}\))65 Multiplication property of equality using the multiplicative inverse of 2
If: 1P = 32.5
Then: P = 32.5 Multiplicative identity
The park pass costs $32.50.
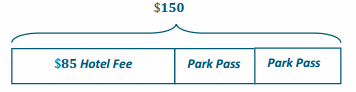
c. Model the problem using a tape diagram to check your work.
Answer:
150 – 85 = 65
65÷2 = 32.50
Suppose you want to buy your favorite ice cream bar while at the amusement park, and it costs $2.89. If you purchase the ice cream bar and 3 bottles of water, pay with a $10 bill, and receive no change, then how much did each bottle of water cost?
d. Write an equation to model this situation.
Answer:
W: the cost of one bottle of water
2.89 + 3W = 10
e. Solve the equation to determine the cost of one water bottle. Then write the reason that justifies each step using if – then statements.
Answer:
If: 2.89 + 3W = 10
Then: 2.89 – 2 .89 + 3W = 10 – 2.89 Subtraction property of equality for the additive inverse of 2.89
If: 0 + 3W = 7.11
Then: 3W = 7.11 Additive identity
If: 3W = 7.11
Then: \(\frac{1}{3}\) (3W) = \(\frac{1}{3}\) (7.11) Multiplication property of equality using the multiplicative inverse of 3
If: 1W = 2.37
Then: W = 2.37 Multiplicative identity
A bottle of water costs $2.37.
f. Model the problem using a tape diagram to check your work.
Answer:
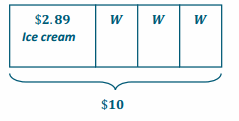
10 – 2.89 = 7.11
\(\frac{7.11}{3}\) = 2.37
Question 2.
Weekly Allowance
Charlotte receives a weekly allowance from her parents. She spent half of this week’s allowance at the movies but earned an additional $4 for performing extra chores. If she did not spend any additional money and finished the week with $12, what is Charlotte’s weekly allowance?
a. Write an equation that can be used to find the original amount of Charlotte’s weekly allowance. Let A be the value of Charlotte’s original weekly allowance.
Answer:
\(\frac{1}{2}\) A + 4 = 12
b. Solve the equation to find the original amount of allowance. Then write the reason that justifies each step using if – then statements.
Answer:
If: \(\frac{1}{2}\) A + 4 = 12
Then: \(\frac{1}{2}\) A + 4 – 4 = 12 – 4 Subtraction property of equality for the additive inverse of 4
If: \(\frac{1}{2}\) A + 0 = 8
Then: \(\frac{1}{2}\) A = 8 Additive identity
If : \(\frac{1}{2}\) A = 8
Then: (2) \(\frac{1}{2}\) A = (2)8 Multiplication property of equality using the multiplicative inverse of \(\frac{1}{2}\)
If: 1A = 16
Then: A = 16 Multiplicative identity
The original allowance was $16.
c. Explain your answer in the context of this problem.
Answer:
Charlotte’s weekly allowance is $16.
d. Charlotte’s goal is to save $100 for her beach trip at the end of the summer. Use the amount of weekly allowance you found in part (c) to write an equation to determine the number of weeks that Charlotte must work to meet her goal. Let w represent the number of weeks.
Answer:
16 w = 100
(\(\frac{1}{16}\))16w = (\(\frac{1}{16}\))100
1w = 6.25
w = 6.25
e. In looking at your answer to part (d) and based on the story above, do you think it will take Charlotte that many weeks to meet her goal? Why or why not?
Answer:
Charlotte needs more than 6 weeks’ allowance, so she will need to save 7 weeks’ allowance (and not spend any of it). There are 10–12 weeks in the summer; so, yes, she can do it.
Exercise 3.
Travel Baseball Team
Allen is very excited about joining a travel baseball team for the fall season. He wants to determine how much money he should save to pay for the expenses related to this new team. Players are required to pay for uniforms, travel expenses, and meals.
a. If Allen buys 4 uniform shirts at one time, he gets a $10.00 discount so that the total cost of 4 shirts would be $44. Write an algebraic equation that represents the regular price of one shirt. Solve the equation. Write the reason that justifies each step using if – then statements.
Answer:
s: the cost of one shirt
If: 4s – 10 = 44
Then: 4s – 10 + 10 = 44 + 10 Addition property of equality using the additive inverse of – 10
If: 4s + 0 = 54
Then: 4s = 54 Additive identity
If: 4s = 54
Then: (\(\frac{1}{4}\))4s = (\(\frac{1}{4}\))54 Multiplication property of equality using multiplicative inverse of 4
If: 1s = 13.50
Then: s = 13.50 Multiplicative identity
b. What is the cost of one shirt without the discount?
Answer:
The cost of one shirt is $13.50.
c. What is the cost of one shirt with the discount?
Answer:
4s = 44
(\(\frac{1}{4}\))4s = (\(\frac{1}{4}\))44
1s = 11
s = 11
The cost of one shirt with the discount is $11.00.
d. How much more do you pay per shirt if you buy them one at a time (rather than in bulk)?
Answer:
13.50 – 11.00 = 2.50
One shirt costs $11 if you buy them in bulk. So, Allen would pay $2.50 more per shirt if he bought them one at a time.
Allen’s team was also required to buy two pairs of uniform pants and two baseball caps, which total $68. A pair of pants costs $12 more than a baseball cap.
e. Write an equation that models this situation. Let c represent the cost of a baseball cap.
Answer:
2(cap + 1 pair of pants) = 68
2(c + c + 12) = 68 or 2 ( 2c + 12) = 68 or 4c + 24 = 68
f. Solve the equation algebraically to find the cost of a baseball cap. Write the reason that justifies each step using if – then statements.
Answer:
If: 2 (2 c + 12) = 68
Then: (\(\frac{1}{2}\))(2 )(2 c + 12) = (\(\frac{1}{2}\))68 Multiplication property of equality using the multiplicative inverse of 2
If: 1(2c + 12) = 34
Then: 2c + 12 = 34 Multiplicative identity
If: 2c + 12 = 34
Then: 2c + 12 – 12 = 34 – 12 Subtraction property of equality for the additive inverse of 12
If: 2c + 0 = 22
Then: 2c = 22 Additive identity
If: 2c = 22
Then: (\(\frac{1}{2}\))2c = (\(\frac{1}{2}\))22 Multiplication property of equality using the multiplicative inverse of 2
If: 1c = 11
Then: c = 11 Multiplicative identity
g. Model the problem using a tape diagram in order to check your work from part (f).
Answer:
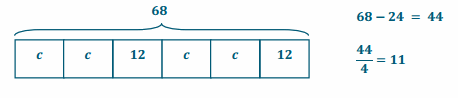
h. What is the cost of one cap?
Answer:
The cost of one cap is $11.
i. What is the cost of one pair of pants?
Answer:
11 + 12 = 23 The cost of one pair of pants is $23.
Eureka Math Grade 7 Module 2 Lesson 23 Problem Set Answer Key
For Exercises 1–4, solve each equation algebraically using if – then statements to justify your steps.
Question 1.
\(\frac{2}{3}\) x – 4 = 20
Answer:
If: \(\frac{2}{3}\) x – 4 = 20
Then: \(\frac{2}{3}\) x – 4 + 4 = 20 + 4 Addition property of equality using the additive inverse of – 4
If: \(\frac{2}{3}\) x + 0 = 24
Then: \(\frac{2}{3}\) x = 24 Additive identity
If: \(\frac{2}{3}\) x = 24
Then: (\(\frac{3}{2}\)) \(\frac{2}{3}\) x = (\(\frac{3}{2}\))24 Multiplication property of equality using the multiplicative inverse of \(\frac{2}{3}\)
If: 1x = 36
Then: x = 36 Multiplicative identity
Question 2.
4 = \(\frac{ – 1 + x}{2}\)
Answer:
If: 4 = \(\frac{ – 1 + x}{2}\)
Then: 2 (4) = 2 (\(\frac{ – 1 + x}{2}\)) Multiplication property of equality using the multiplicative inverse of \(\frac{1}{2}\)
If: 8 = 1 ( – 1 + x)
Then: 8 = – 1 + x Multiplicative identity
If: 8 = – 1 + x
Then: 8 – ( – 1) = – 1 – ( – 1) + x Subtraction property of equality for the additive inverse of – 1
If: 9 = 0 + x
Then: 9 = x Additive identity
Question 3.
12(x + 9) = – 108
Answer:
If: 12(x + 9) = – 108
Then: (\(\frac{1}{12}\))12(x + 9) = (\(\frac{1}{12}\))( – 108) Multiplication property of equality using the multiplicative inverse of 12
If: 1 (x + 9) = – 9
Then: x + 9 = – 9 Multiplicative identity
If: x + 9 = – 9
Then: x + 9 – 9 = – 9 – 9 Subtraction property of equality for the additive inverse of 9
If: x + 0 = – 18
Then: x = – 18 Additive identity
Question 4.
5x + 14 = – 7
Answer:
If: 5x + 14 = – 7
Then: 5x + 14 – 14 = – 7 – 14 Subtraction property of equality for the additive inverse of 14
If: 5x + 0 = – 21
Then: 5x = – 21 Additive identity
If: 5x = – 21
Then: (\(\frac{1}{5}\))5x = (\(\frac{1}{5}\))( – 21) Multiplication property of equality using the multiplicative inverse of 5
If: 1x = – 4.2
Then: x = – 4.2 Multiplicative identity
For Exercises 5–7, write an equation to represent each word problem. Solve the equation showing the steps, and then state the value of the variable in the context of the situation.
Question 5.
A plumber has a very long piece of pipe that is used to run city water parallel to a major roadway. The pipe is cut into two sections. One section of pipe is 12 ft. shorter than the other. If \(\frac{3}{4}\) of the length of the shorter pipe is
120 ft., how long is the longer piece of the pipe?
Answer:
Let x represent the longer piece of pipe.
If: \(\frac{3}{4}\)(x – 12) = 120
Then: \(\frac{4}{3}\) (\(\frac{3}{4}\))(x – 12) = (\(\frac{4}{3}\))120 Multiplication property of equality using the multiplicative inverse of \(\frac{3}{4}\)
If: 1(x – 12) = 160
Then: x – 12 = 160 Multiplicative identity
If: x – 12 = 160
Then: x – 12 + 12 = 160 + 12 Addition property of equality for the additive inverse of – 12
If: x + 0 = 172
Then: x = 172 Additive identity
The longer piece of pipe is 172 ft.
Question 6.
Bob’s monthly phone bill is made up of a $10 fee plus $0.05 per minute. Bob’s phone bill for July was $22. Write an equation to model the situation using m to represent the number of minutes. Solve the equation to determine the number of phone minutes Bob used in July.
Answer:
Let m represent the number of phone minutes Bob used.
If: 10 + 0.05m = 22
Then: 10 – 10 + 0.05m = 22 – 10 Subtraction property of equality for the additive inverse of 10
If: 0 + 0.05m = 12
Then: 0.05m = 12 Additive identity
If: 0.05m = 12
Then: (\(\frac{1}{0.05}\))0.05m = (\(\frac{1}{0.05}\))12 Multiplication property of equality using the multiplicative inverse of 0.05
If: 1m = 240
Then: m = 240 Multiplicative identity
Bob used 240 phone minutes in July.
Question 7.
Kym switched cell phone plans. She signed up for a new plan that will save her $3.50 per month compared to her old cell phone plan. The cost of the new phone plan for an entire year is $294. How much did Kym pay per month under her old phone plan?
Answer:
Let n represent the amount Kym paid per month for her old cell phone plan.
If: 294 = 12(n – 3.50)
Then: (\(\frac{1}{12}\))(294) = (\(\frac{1}{12}\))12(n – 3.50) Multiplication property of equality using the multiplicative inverse of 12
If: 24.5 = 1 (n – 3.50)
Then: 24.5 = n – 3.50 Multiplicative identity
If: 24.5 = n – 3.50
Then: 24.5 + 3.50 = n – 3.50 + 3.50 Addition property of equality for the additive inverse of – 3.50
If: 28 = n + 0
Then: 28 = n Additive identity
Kym paid $28 per month for her old cell phone plan.
Eureka Math Grade 7 Module 2 Lesson 23 Exit Ticket Answer Key
Andrew’s math teacher entered the seventh – grade students in a math competition. There was an enrollment fee of $30 and also an $11 charge for each packet of 10 tests. The total cost was $151. How many tests were purchased?
Set up an equation to model this situation, solve it using if – then statements, and justify the reasons for each step in your solution.
Answer:
Let p represent the number of test packets.
Enrollment fee + cost of test = 151
If: 30 + 11p = 151
Then: 30 – 30 + 11p = 151 – 30 Subtraction property of equality for the additive inverse of 30
If: 0 + 11p = 121
Then: 11p = 121 Additive identity
If: 11p = 121
Then: \(\frac{1}{11}\) (11p) = \(\frac{1}{11}\) (121) Multiplication property of equality using the multiplicative inverse of 11
If: 1p = 11
Then: p = 11 Multiplicative identity
Andrew’s math teacher bought 11 packets of tests. There were 10 tests in each packet, and 10×11 = 110.
So, there were 110 tests purchased.