Engage NY Eureka Math 7th Grade Module 2 Lesson 8 Answer Key
Eureka Math Grade 7 Module 2 Lesson 8 Example Answer Key
Example 1.
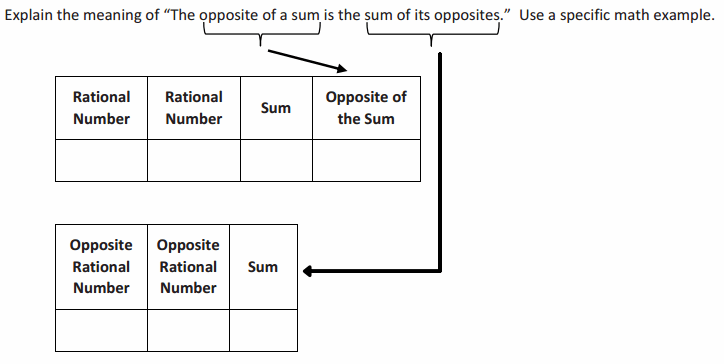
Answer:
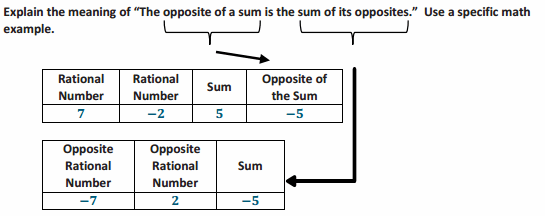
It means that if you have a sum and want to take the opposite, for instance, -(7 + (-2)), you can rewrite it as the sum of each addend’s opposite, -7 + 2.
Example 2.
A Mixed Number Is a Sum
Use the number line model shown below to explain and write the opposite of 2\(\frac{2}{5}\) as a sum of two rational numbers.
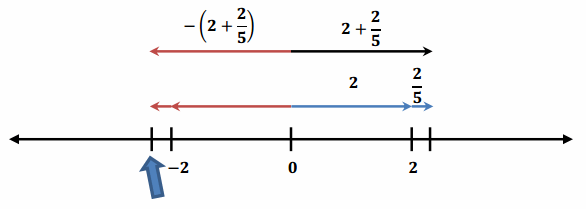
The opposite of a sum (top single arrow pointing left) and the sum of the opposites correspond to the same point on the number line.
Answer:
The opposite of 2\(\frac{2}{5}\) is -2 \(\frac{2}{5}\) .
-2 \(\frac{2}{5}\) written as the sum of two rational numbers is -2 + (-\(\frac{2}{5}\)).
Eureka Math Grade 7 Module 2 Lesson 8 Exercise Answer Key
Exercise 1.
Represent the following expression with a single rational number.
-2\(\frac{2}{5}\) + \(\frac{1}{4}\) – \(\frac{3}{5}\)
Answer:
Two Possible Methods:
-2\(\frac{8}{20}\) + 3\(\frac{5}{20}\) – \(\frac{12}{20}\)
–\(\frac{48}{20}\) + \(\frac{65}{20}\) – \(\frac{12}{20}\)
\(\frac{17}{20}\) – \(\frac{12}{20}\)
\(\frac{5}{20}\) or \(\frac{1}{4}\)
OR
-2\(\frac{2}{5}\) + 3\(\frac{1}{4}\) + (-\(\frac{3}{5}\))
-2\(\frac{2}{5}\) + (-\(\frac{3}{5}\)) + 3\(\frac{1}{4}\) commutative property
-2\(\frac{5}{5}\) + 3\(\frac{1}{4}\)
-3 + 3\(\frac{1}{4}\)
\(\frac{1}{4}\)
Exercise 2.
Rewrite each mixed number as the sum of two signed numbers.
a. -9\(\frac{5}{8}\)
Answer:
-9 + (-\(\frac{5}{8}\) )
b. -2\(\frac{1}{2}\)
Answer:
-2 + (-\(\frac{1}{2}\) )
c. 8\(\frac{11}{12}\)
8 + \(\frac{11}{12}\)
Exercise 3.
Represent each sum as a mixed number.
a. -1 + (-\(\frac{5}{12}\))
Answer:
-1 \(\frac{5}{12}\)
b. 30 + \(\frac{1}{8}\)
Answer:
30\(\frac{1}{8}\)
c. -17 + (-\(\frac{1}{9}\) )
-17 \(\frac{1}{9}\)
Note: Exercises 3 and 4 are designed to provide students with an opportunity to practice writing mixed numbers as sums so they can do so as the need arises in more complicated problems.
Exercise 4.
Mr. Mitchell lost 10 pounds over the summer by jogging each week. By winter, he had gained 5 \(\frac{1}{8}\) pounds. Represent this situation with an expression involving signed numbers. What is the overall change in Mr. Mitchell’s weight?
Answer:
-10 + 5 \(\frac{1}{8}\)
= -10 + 5 + \(\frac{1}{8}\)
=(-10 + 5) + \(\frac{1}{8}\)
=(-5) + \(\frac{1}{8}\)
= -4\(\frac{7}{8}\)
Mr. Mitchell’s weight dropped by 4 \(\frac{7}{8}\) pounds.
Exercise 5.
Jamal is completing a math problem and represents the expression -5\(\frac{5}{7}\) + 8 – 3\(\frac{2}{7}\) with a single rational number as shown in the steps below. Justify each of Jamal’s steps. Then, show another way to solve the problem.
= -5 \(\frac{5}{7}\) + 8 + (-3 \(\frac{2}{7}\) )
= -5 \(\frac{5}{7}\) + (-3 \(\frac{2}{7}\) ) + 8
= -5 + (-\(\frac{5}{7}\) ) + (-3) + (-\(\frac{2}{7}\) ) + 8
= -5 + (-\(\frac{5}{7}\) ) + (-\(\frac{2}{7}\) ) + (-3) + 8
= -5 + (-1) + (-3) + 8
= -6 + (-3) + 8
= (-9) + 8
= -1
Answer:
Step 1: Subtracting a number is the same as adding its inverse.
Step 2: Apply the commutative property of addition.
Step 3: The opposite of a sum is the sum of its opposites.
Step 4: Apply the commutative property of addition.
Step 5: Apply the associative property of addition.
(-\(\frac{5}{7}\)) + (-\(\frac{2}{7}\) ) = (-\(\frac{7}{7}\) )= -1
Step 6: -5 + (-1) = -6
Step 7: -6 + -3 = -9
Step 8: -9 + 8= -1
Answers will vary for other methods of reaching a single rational number. Students may choose to add -5 \(\frac{5}{7}\) and 8 together first, but a common mistake is to represent their sum as 3 \(\frac{5}{7}\) , rather than 2 \(\frac{2}{7}\) .
Eureka Math Grade 7 Module 2 Lesson 8 Problem Set Answer Key
Question 1.
Represent each sum as a single rational number.
a. -14 + (-\(\frac{8}{9}\) )
Answer:
-14 \(\frac{8}{9}\)
b. 7 + \(\frac{1}{9}\)
Answer:
7 \(\frac{1}{9}\)
c. -3 + (-\(\frac{1}{6}\) )
Answer:
-3 \(\frac{1}{6}\)
Rewrite each of the following to show that the opposite of a sum is the sum of the opposites. Problem 2 has been completed as an example.
Question 2.
-(9 + 8) = -9 + (-8)
-17 = -17
Answer:
Answer provided in student materials.
Question 3.
-(\(\frac{1}{4}\) + 6) = –\(\frac{1}{4}\) + (-6)
Answer:
-6 \(\frac{1}{4}\) = -6 \(\frac{1}{4}\)
Question 4.
-(10 + (-6)) = -10 + 6
Answer:
– 4 = -4
Question 5.
-((-55) + \(\frac{1}{2}\)) = 55 + (-\(\frac{1}{2}\) )
Answer:
54\(\frac{1}{2}\) = 54\(\frac{1}{2}\)
Use your knowledge of rational numbers to answer the following questions.
Question 6.
Meghan said the opposite of the sum of -12 and 4 is 8. Do you agree? Why or why not?
Answer:
Yes, I agree. The sum of -12 and 4 is -8, and the opposite of -8 is 8.
Question 7.
Jolene lost her wallet at the mall. It had $10 in it. When she got home, her brother felt sorry for her and gave her $5.75. Represent this situation with an expression involving rational numbers. What is the overall change in the amount of money Jolene has?
Answer:
-10 + 5.75 = -4.25. The overall change in the amount of money Jolene has is -4.25 dollars.
Question 8.
Isaiah is completing a math problem and is at the last step: 25 – 28\(\frac{1}{5}\). What is the answer? Show your work.
Answer:
25 – 28 \(\frac{1}{5}\) = 25 + (-28 + (-\(\frac{1}{5}\))) = (25 + -28) + (-\(\frac{1}{5}\)) = -3\(\frac{1}{5}\)
Question 9.
A number added to its opposite equals zero. What do you suppose is true about a sum added to its opposite? Use the following examples to reach a conclusion. Express the answer to each example as a single rational number.
Answer:
A sum added to its opposite is zero.
a. (3 + 4) + (-3 + -4)
Answer:
(3 + 4) + (-3 + -4) = 7 + (-7) = 0
b. (-8 + 1) + (8 + (- 1))
Answer:
(-8 + 1) + (8 + (- 1)) = (-7) + 7 = 0
c. (-\(\frac{1}{2}\) + (-\(\frac{1}{4}\) )) + (\(\frac{1}{2}\) + \(\frac{1}{4}\) )
Answer:
(-\(\frac{1}{2}\) + (-\(\frac{1}{4}\) )) + (\(\frac{1}{2}\) + \(\frac{1}{4}\) ) = (-\(\frac{3}{4}\) ) + \(\frac{3}{4}\) =0
Eureka Math Grade 7 Module 2 Lesson 8 Integer Addition—Round 1 Answer Key
Directions: Determine the sum of the integers, and write it in the column to the right.

Answer:
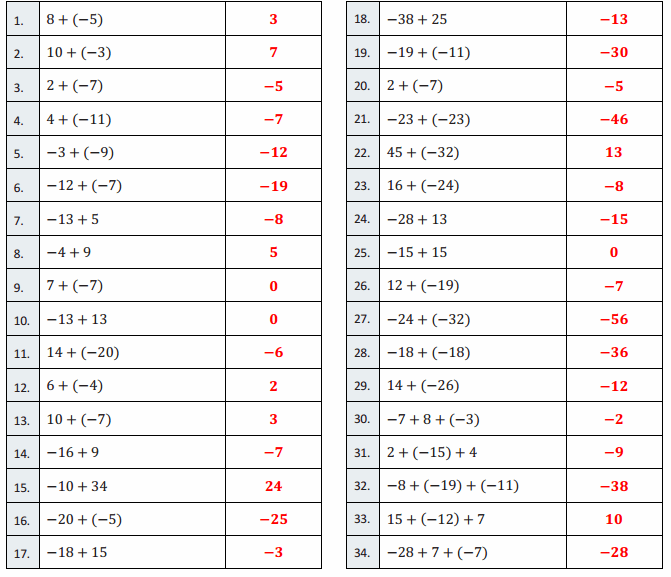
Question 1.
8 + (-5)
Answer:
3
Question 2.
10 + (-3)
Answer:
7
Question 3.
2 + (-7)
Answer:
-5
Question 4.
4 + (-11)
Answer:
-7
Question 5.
-3 + (-9)
Answer:
-12
Question 6.
-12 + (-7)
Answer:
-19
Question 7.
-13 + 5
Answer:
0
Question 8.
-4 + 9
Answer:
5
Question 9.
7 + (-7)
Answer:
0
Question 10.
-13 + 13
Answer:
0
Question 11.
14 + (-20)
Answer:
-6
Question 12.
6 + (-4)
Answer:
2
Question 13.
10 + (-7)
Answer:
3
Question 14.
-16 + 9
Answer:
-7
Question 15.
-10 + 34
Answer:
24
Question 16.
-20 + (-5)
Answer:
-25
Question 17.
-18 + 15
Answer:
-3
Question 18.
-38 + 25
Answer:
-13
Question 19.
-19 + (-11)
Answer:
-30
Question 20.
2 + (-7)
Answer:
-5
Question 21.
-23 + (-23)
Answer:
-46
Question 22.
45 + (-32)
Answer:
13
Question 23.
16 + (-24)
Answer:
-8
Question 24.
-28 + 13
Answer:
-15
Question 25.
-15 + 15
Answer:
0
Question 26.
12 + (-19)
Answer:
-7
Question 27.
-24 + (-32)
Answer:
-56
Question 28.
-18 + (-18)
Answer:
-36
Question 29.
14 + (-26)
Answer:
-12
Question 30.
-7 + 8 + (-3)
Answer:
-2
Question 31.
2 + (-15) + 4
Answer:
-9
Question 32.
-8 + (-19) + (-11)
Answer:
-38
Question 33.
15 + (-12) + 7
Answer:
10
Question 34.
-28 + 7 + (-7)
Answer:
-28
Eureka Math Grade 7 Module 2 Lesson 8 Integer Addition—Round 2 Answer Key

Answer:
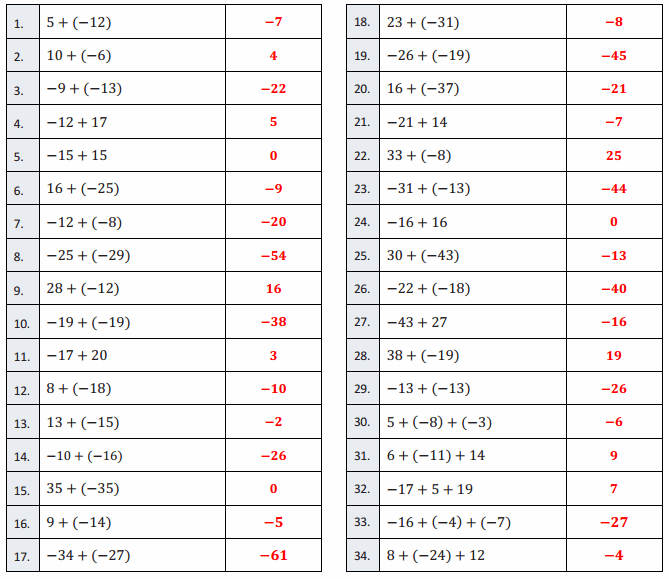
Question 1.
5 + (-12)
Answer:
-7
Question 2.
10 + (-6)
Answer:
4
Question 3.
-9 + (-13)
Answer:
-22
Question 4.
-12 + 17
Answer:
5
Question 5.
-15 + 15
Answer:
0
Question 6.
16 + (-25)
Answer:
-9
Question 7.
-12 + (-8)
Answer:
-20
Question 8.
-25 + (-29)
Answer:
-54
Question 9.
28 + (-12)
Answer:
16
Question 10.
-19 + (-19)
Answer:
-38
Question 11.
-17 + 20
Answer:
3
Question 12.
8 + (-18)
Answer:
-10
Question 13.
13 + (-15)
Answer:
-2
Question 14.
-10 + (-16)
Answer:
-26
Question 15.
35 + (-35)
Answer:
0
Question 16.
9 + (-14)
Answer:
-5
Question 17.
-34 + (-27)
Answer:
-61
Question 18.
23 + (-31)
Answer:
-8
Question 19.
-26 + (-19)
Answer:
-45
Question 20.
16 + (-37)
Answer:
-21
Question 21.
-21 + 14
Answer:
-7
Question 22.
33 + (-8)
Answer:
25
Question 23.
-31 + (-13)
Answer:
-44
Question 24.
-16 + 16
Answer:
0
Question 25.
30 + (-43)
Answer:
-13
Question 26.
-22 + (-18)
Answer:
-40
Question 27.
-43 + 27
Answer:
-16
Question 28.
38 + (-19)
Answer:
19
Question 29.
-13 + (-13)
Answer:
-26
Question 30.
5 + (-8) + (-3)
Answer:
-6
Question 31.
6 + (-11) + 14
Answer:
9
Question 32.
-17 + 5 + 19
Answer:
7
Question 33.
-16 + (-4) + (-7)
Answer:
-27
Question 34.
8 + (-24) + 12
Answer:
-4
Eureka Math Grade 7 Module 2 Lesson 8 Exit Ticket Answer Key
Mariah and Shane both started to work on a math problem and were comparing their work in math class. Are both of their representations correct? Explain, and finish the math problem correctly to arrive at the correct answer.

Mariah started the problem as follows:
-5 – (-1\(\frac{3}{4}\) )
= -5 + 1 – \(\frac{3}{4}\)
Shane started the problem as follows:
-5 – (-1\(\frac{3}{4}\) )
= -5 + (1 \(\frac{3}{4}\))
= -5 + (1 + \(\frac{3}{4}\))
Answer:
Shane’s method is correct. In Mariah’s math work, she only dealt with part of the mixed number. The fractional part should have been positive too because the opposite of -1 \(\frac{3}{4}\) is 1 \(\frac{3}{4}\) , which contains both a positive 1 and a positive \(\frac{3}{4}\) .
The correct work would be
-5 – (-1\(\frac{3}{4}\)) = -5 + (1 \(\frac{3}{4}\)) = -5 + (1 + \(\frac{3}{4}\)) = (-5 + 1) + \(\frac{3}{4}\) = -4 + \(\frac{3}{4}\) = -3\(\frac{1}{4}\) .
The rational number would be -3 \(\frac{1}{4}\) , which means Jessica’s friend gave away 3 \(\frac{1}{4}\) dollars, or $3.25.