Engage NY Eureka Math 7th Grade Module 4 Lesson 12 Answer Key
Eureka Math Grade 7 Module 4 Lesson 12 Example Answer Key
Example 1.
Create a snowman on the accompanying grid. Use the octagon given as the middle of the snowman with the following conditions:
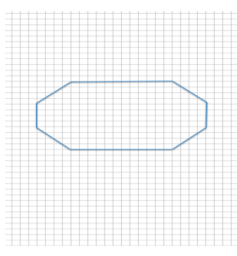
a. Calculate the width, neck, and height, in units, for the figure to the right.
Answer:
Width: 20
Neck: 12
Height: 12
b. To create the head of the snowman, make a scale drawing of the middle of the snowman with a scale factor of 75%. Calculate the new lengths, in units, for the width, neck, and height.
Answer:
Width: 75%(20) = (0.75)(20) = 15
Neck: 75%(12) = (0.75)(12) = 9
Height : 75%(12) = (0.75)(12) = 9
c. To create the bottom of the snowman, make a scale drawing of the middle of the snowman with a scale factor of 125%. Calculate the new lengths, in units, for the width, waist, and height.
Answer:
Width: 125%(20) = (1.25)(20) = 25
Waist: 125%(12) = (1.25)(12) = 15
Height: 125%(12) = (1.25)(12) = 15
d. Is the head a reduction or an enlargement of the middle?
Answer:
The head is a reduction of the middle since the lengths of the sides are smaller than the lengths in the original drawing and the scale factor is less than 100% (75%).
e. Is the bottom a reduction or an enlargement of the middle?
Answer:
The bottom is an enlargement of the middle since the lengths of the scale drawing are larger than the lengths in the original drawing, and the scale factor is greater than 100% (125%).
f. What is the significance of the scale factor as it relates to 100%? What happens when such scale factors are applied?
Answer:
A scale factor of 100% would create a drawing that is the same size as the original drawing; therefore, it would be neither an enlargement nor reduction. A scale factor of less than 100% results in a scale drawing that is a reduction of the original drawing. A scale factor of greater than 100% results in a scale drawing that is an enlargement of the original drawing.
g. Use the dimensions you calculated in parts (b) and (c) to draw the complete snowman.
Answer:
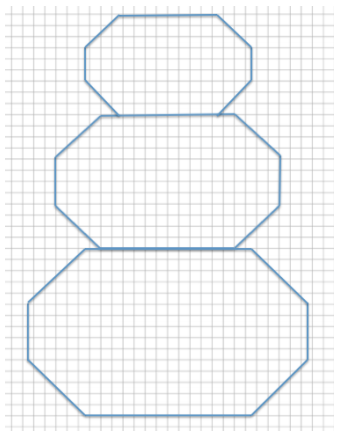
Example 2.
Create a scale drawing of the arrow below using a scale factor of 150%.
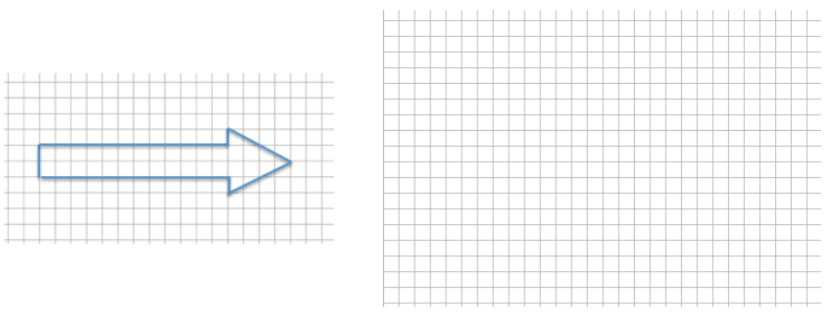
Answer:
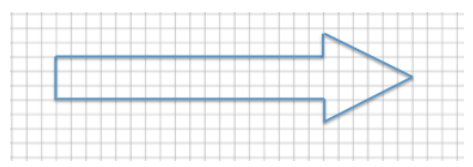
Example 3: Scale Drawings Where the Horizontal and Vertical Scale Factors Are Different
Sometimes it is helpful to make a scale drawing where the horizontal and vertical scale factors are different, such as when creating diagrams in the field of engineering. Having differing scale factors may distort some drawings.
For example, when you are working with a very large horizontal scale, you sometimes must exaggerate the vertical scale in order to make it readable. This can be accomplished by creating a drawing with two scales. Unlike the scale drawings with just one scale factor, these types of scale drawings may look distorted. Next to the drawing below is a scale drawing with a horizontal scale factor of 50% and vertical scale factor of 25% (given in two steps). Explain how each drawing is created.
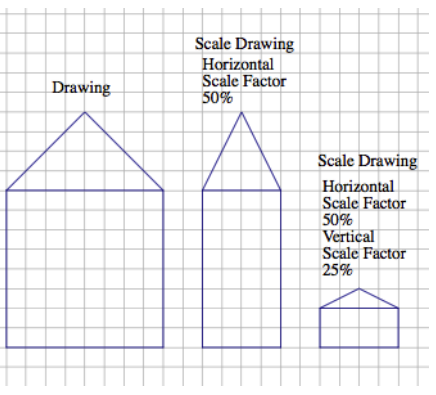
Answer:
Each horizontal distance in the scale drawing is 50%
(or half) of the corresponding length in the original drawing. Each vertical distance in the scale drawing is 25% (or one-fourth) of the corresponding length in the original drawing.
Horizontal distance of house: 8(0.50) = 8(\(\frac{1}{2}\)) = 4
Vertical distance of house: 8(0.25) = 8(\(\frac{1}{4}\)) = 2
Vertical distance of top of house:
4(0.25) = 4(\(\frac{1}{4}\)) = 1
Eureka Math Grade 7 Module 4 Lesson 12 Exercise Answer Key
Opening Exercise:
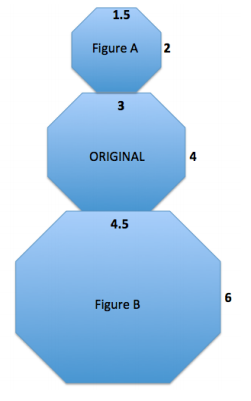
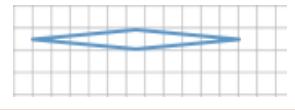
Compare the corresponding lengths of Figure A to the original octagon in the middle. This is an example of a particular type of scale drawing called a _________. Explain why it is called that.
Answer:
reduction
A scale drawing is a reduction of the original drawing when the side lengths of the scale drawing are smaller than the corresponding side lengths of the original figure or drawing.
Compare the corresponding lengths of Figure B to the original octagon in the middle. This is an example of a particular type of scale drawing called an __________. Explain why it is called that.
Answer:
enlargement
A scale drawing is an enlargement of the original drawing when the side lengths of the scale drawing are larger than the corresponding side lengths of the original figure or drawing.
The scale factor is the quotient of any length in the scale drawing and its corresponding length in the original drawing.
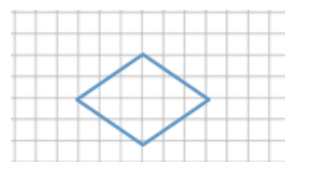
Use what you recall from Module 1 to determine the scale factors between the original figure and Figure A and the original figure and Figure B.
Answer:
Scale factor between original and Figure A: \(\frac{1.5}{3}\) = \(\frac{1}{2}\) or \(\frac{2}{4}\) = \(\frac{1}{2}\)
Scale factor between original and Figure B: \(\frac{4.5}{3}\) = \(\frac{3}{2}\) or \(\frac{6}{4}\) = \(\frac{3}{2}\)
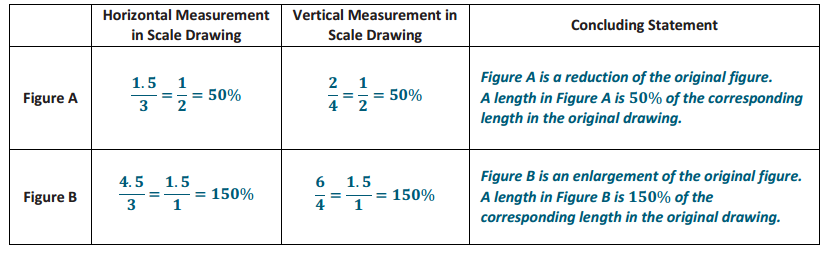
Use the diagram to complete the chart below to determine the horizontal and vertical scale factors. Write answers as a percent and as a concluding statement using the previously learned reduction and enlargement vocabulary.
Answer:
Exercise 1.
Create a scale drawing of the following drawing using a horizontal scale factor of 183 \(\frac{1}{3}\)% and a vertical scale factor of 25%.
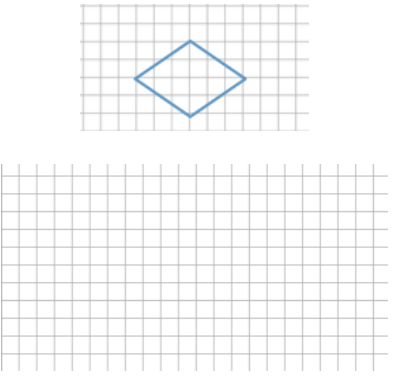
Answer:
Horizontal scale factor: \(\frac{183 \frac{1}{3} \cdot 3}{100 \cdot 3}\) = \(\frac{550}{300}\) = \(\frac{11}{6}\)
Horizontal distance: 6(\(\frac{11}{6}\)) = 11
Vertical scale factor: \(\frac{25}{100}\) = \(\frac{1}{4}\)
Vertical distance: 4(\(\frac{1}{4}\)) = 1
New sketch:
Exercise 2.
Chris is building a rectangular pen for his dog. The dimensions are 12 units long and 5 units wide.

Chris is building a second pen that is 60% the length of the original and 125% the width of the original. Write equations to determine the length and width of the second pen.
Answer:
Length: 12 × 0.60 = 7.2
The length of the second pen is 7.2 units.
Width: 5 × 1.25 = 6.25
The width of the second pen is 6.25 units.
Eureka Math Grade 7 Module 4 Lesson 12 Problem Set Answer Key
Question 1.
Use the diagram below to create a scale drawing using a scale factor of 133 \(\frac{1}{3}\)%. Write numerical equations to find the horizontal and vertical distances in the scale drawing.
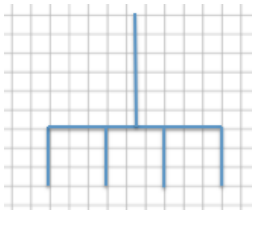
Answer:
Scale factor: 133 \(\frac{133 \frac{1}{3} \cdot 3}{100 \cdot 3}\) = \(\frac{400}{300}\) = \(\frac{4}{3}\)
Horizontal distance: 9(\(\frac{4}{3}\)) = 12
Vertical distance forks: 3(\(\frac{4}{3}\)) = 4
Vertical distance handle: 6(\(\frac{4}{3}\)) = 8
Scale drawing:
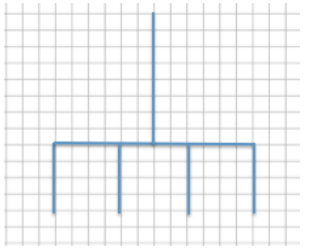
Question 2.
Create a scale drawing of the original drawing given below using a horizontal scale factor of 80% and a vertical scale factor of 175%. Write numerical equations to find the horizontal and vertical distances.
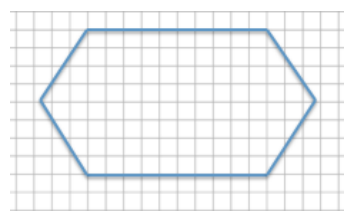
Answer:
Horizontal scale factor: 80% = \(\frac{80}{100}\) = \(\frac{4}{5}\)
Horizontal segment lengths: 10(0.80) = 8 or 10(\(\frac{4}{5}\)) = 8
Horizontal distance: 15(\(\frac{4}{5}\)) = 12
Vertical scale factor: 175% = \(\frac{175}{100}\) = \(\frac{7}{4}\)
Vertical distance: 8(\(\frac{7}{4}\)) = 14
Scale drawing:
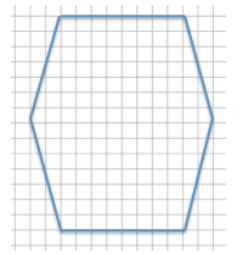
Question 3.
The accompanying diagram shows that the length of a pencil from its eraser to its tip is 7 units and that the eraser is 1.5 units wide. The picture was placed on a photocopy machine and reduced to 66 2/3%. Find the new size of the pencil, and sketch a drawing. Write numerical equations to find the new dimensions.

Answer:
Scale factor: 66 \(\frac{2}{3}\)% = \(\frac{66 \frac{2}{3} \cdot 3}{100 \cdot 3}\) = \(\frac{200}{300}\) = \(\frac{2}{3}\)
Pencil length: 7(\(\frac{2}{3}\)) = 4 \(\frac{2}{3}\)
Eraser: (1 \(\frac{1}{2}\))(\(\frac{2}{3}\)) = (\(\frac{3}{2}\))(\(\frac{2}{3}\)) = 1

Question 4.
Use the diagram to answer each question.
a. What are the corresponding horizontal and vertical distances in a scale drawing if the scale factor is 25%? Use numerical equations to find your answers.
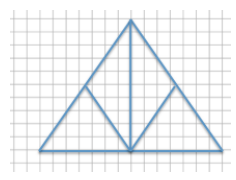
Answer:
Horizontal distance on original drawing: 14
Vertical distance on original drawing: 10
Scale drawing:
Scale factor: 25%
\(\frac{25}{100}\) = \(\frac{1}{4}\)
Horizontal distance: 14(\(\frac{1}{4}\)) = 3.5
Vertical distance: 10(\(\frac{1}{4}\)) = 2.5
b. What are the corresponding horizontal and vertical distances in a scale drawing if the scale factor is 160%? Use a numerical equation to find your answers.
Answer:
Horizontal distance on original drawing: 14
Vertical distance on original drawing: 10
Scale drawing:
Scale factor: 160%
\(\frac{160}{100}\) = \(\frac{8}{5}\)
Horizontal distance: 14(\(\frac{8}{5}\)) = 22.4
Vertical distance: 10(\(\frac{8}{5}\)) = 16
Question 5.
Create a scale drawing of the original drawing below using a horizontal scale factor of 200% and a vertical scale factor of 250%.
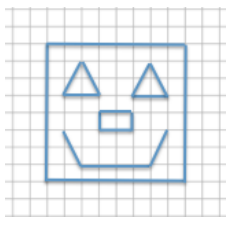
Answer:

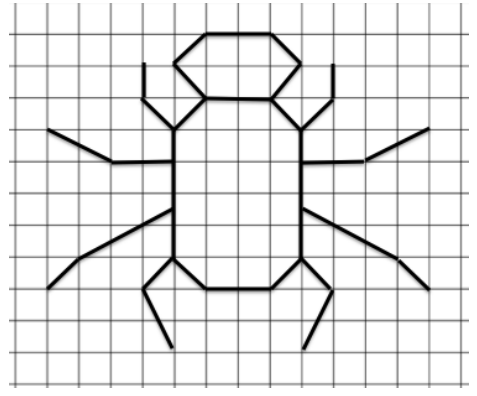
Question 6.
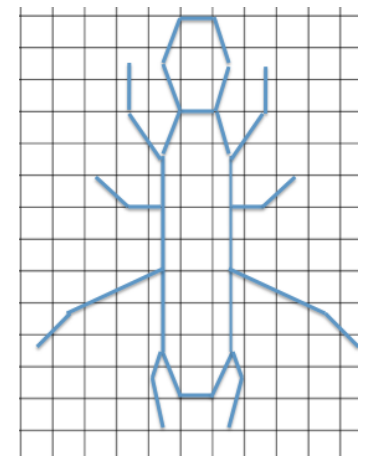
Using the diagram below, on grid paper sketch the same drawing using a horizontal scale factor of 50% and a vertical scale factor of 150%.
Answer:
Eureka Math Grade 7 Module 4 Lesson 12 Exit Ticket Answer Key
Question 1.
Create a scale drawing of the picture below using a scale factor of 60%. Write three equations that show how you determined the lengths of three different parts of the resulting picture.
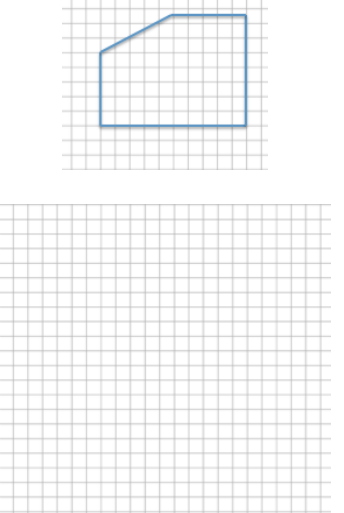
Answer:
Scale factor: 60% = \(\frac{60}{100}\) = \(\frac{3}{5}\)
Horizontal distances: 10(\(\frac{3}{5}\)) = 6
5(\(\frac{3}{5}\)) = 3
Vertical distances: 5(\(\frac{3}{5}\)) = 3
7 \(\frac{1}{2}\) (\(\frac{3}{5}\)) = \(\frac{15}{2}\) (\(\frac{3}{5}\)) = \(\frac{9}{2}\) = 4.5
Scale drawing:
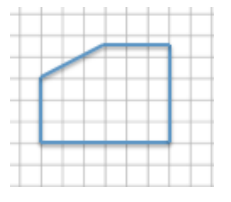
Equations:
Left vertical distance: 5 × 0.60 = 3
Right vertical distance: 7.5 × 0.60 = 4.5
Top horizontal distance: 5 × 0.60 = 3
Bottom horizontal distance: 10 × 0.60 = 6
Question 2.
Sue wants to make two picture frames with lengths and widths that are proportional to the ones given below.
Note: The illustration shown below is not drawn to scale.
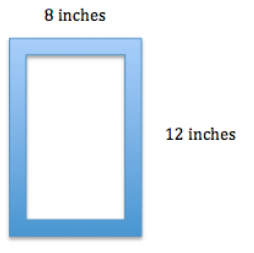
a. Sketch a scale drawing using a horizontal scale factor of 50% and a vertical scale factor of 75%. Determine the dimensions of the new picture frame.
Answer:

Horizontal measurement: 8(0.50) = 4
Vertical measurement: 12(0.75) = 9
4 in. by 9 in.
b. Sketch a scale drawing using a horizontal scale factor of 125% and a vertical scale factor of 140%. Determine the dimensions of the new picture frame.
Answer:

Horizontal measurement: 8(1.25) = 10
Vertical measurement: 12(1.40) = 16.8
10 in. by 16.8 in.
