Engage NY Eureka Math 7th Grade Module 4 Lesson 13 Answer Key
Eureka Math Grade 7 Module 4 Lesson 13 Example Answer Key
Example 1.
The scale factor from Drawing 1 to Drawing 2 is 60%. Find the scale factor from Drawing 2 to Drawing 1. Explain your reasoning.

Answer:
The scale drawing from Drawing 2 to Drawing 1 is an enlargement. Drawing 1 is represented by 100%, and Drawing 2, a reduction of Drawing 1, is represented by 60%. A length in Drawing 2 is the whole, so the scale factor from Drawing 2 to 1 is length in Drawing 1 = percent × length in Drawing 2.
100% = percent × 60%
\(\frac{100 \%}{60 \%}\) = \(\frac{1}{0.60}\) = \(\frac{1}{\frac{3}{5}}\) = \(\frac{5}{3}\) = 166 \(\frac{2}{3}\)%
Example 2.
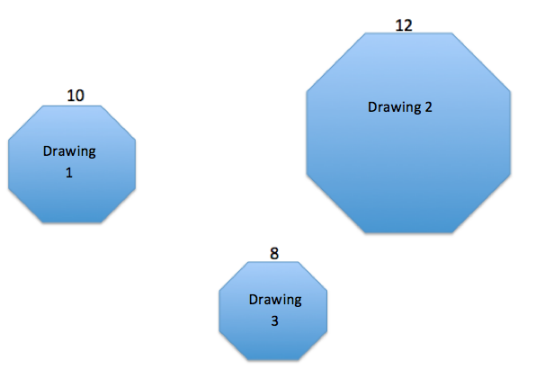
A regular octagon is an eight-sided polygon with side lengths that are all equal. All three octagons are scale drawings of each other. Use the chart and the side lengths to compute each scale factor as a percent. How can we check our answers?
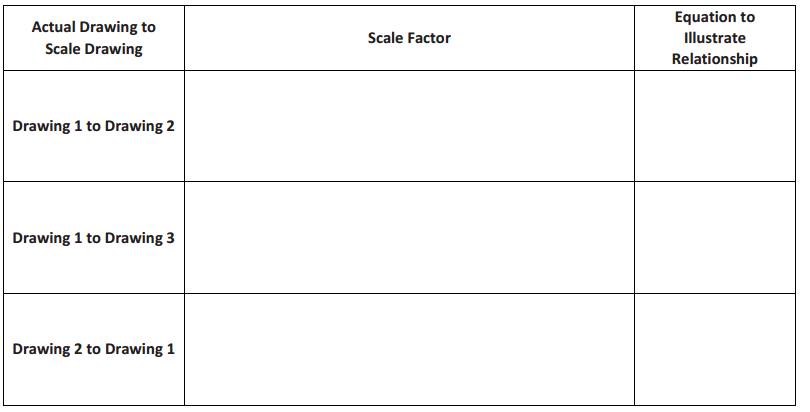

Answer:


To check our answers, we can start with 10 (the length of the original Drawing 1) and multiply by the scale factors we found to see whether we get the corresponding lengths in Drawings 2 and 3.
Drawing 1 to 2: 10(1.20) = 12
Drawing 2 to 3: 12(\(\frac{2}{3}\)) = 8
Example 3.
The scale factor from Drawing 1 to Drawing 2 is 112%, and the scale factor from Drawing 1 to Drawing 3 is 84%. Drawing 2 is also a scale drawing of Drawing 3. Is Drawing 2 a reduction or an enlargement of Drawing 3? Justify your answer using the scale factor. The drawing is not necessarily drawn to scale.
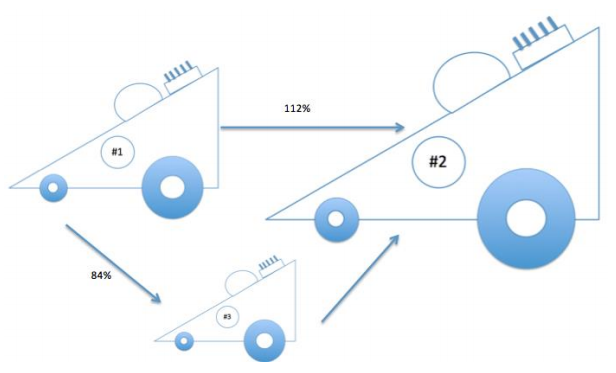
Answer:
First, I needed to find the scale factor of Drawing 3 to Drawing 2 by using the relationship
Quantity = Percent × Whole.
Drawing 3 is the whole. Therefore,
Drawing 2 = Percent × Drawing 3
112% = Percent × 84%
\(\frac{1.12}{0.84}\) = \(\frac{112}{84}\) = \(\frac{4}{3}\) = 133 \(\frac{1}{3}\)%
Since the scale factor is greater than 100%, Drawing 2 is an enlargement of Drawing 3.
Explain how you could use the scale factors from Drawing 1 to Drawing 2 (112%) and from Drawing 2 to Drawing 3 (75%) to show that the scale factor from Drawing 1 to Drawing 3 is 84%.
Answer:
The scale factor from Drawing 1 to Drawing 2 is 112%, and the scale factor from Drawing 2 to Drawing 3 is 75%; therefore, I must find 75% of 112% to get from Drawing 2 to Drawing 3. (0.75)(1.12) = 0.84. Comparing this answer to the original problem, the resulting scale factor is indeed what was given as the scale factor from Drawing 1 to
Drawing 3.
Eureka Math Grade 7 Module 4 Lesson 13 Exercise Answer Key
Opening Exercise
Scale factor: \(\frac{\text { length in SCALE drawing }}{\text { Corresponding length in ORIGINAL drawing }}\)
Describe, using percentages, the difference between a reduction and an enlargement.
Answer:
A scale drawing is a reduction of the original drawing when the lengths of the scale drawing are smaller than the lengths in the original drawing. The scale factor is less than 100%.
A scale drawing is an enlargement of the original drawing when the lengths of the scale drawing are greater than the lengths in the original drawing. The scale factor is greater than 100%.
Use the two drawings below to complete the chart. Calculate the first row (Drawing 1 to Drawing 2) only.

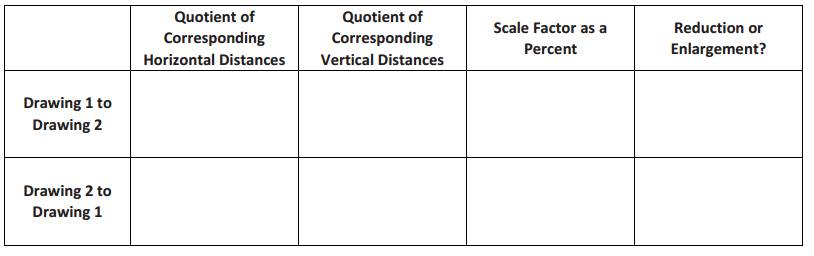
Answer:
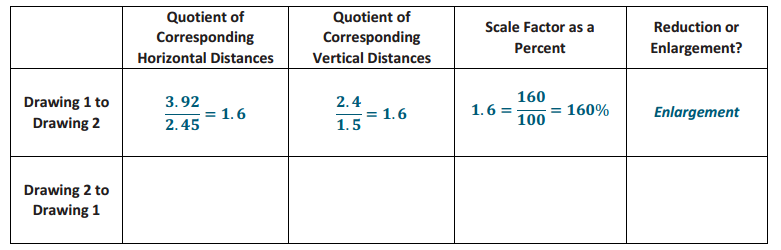
Compare Drawing 2 to Drawing 1. Using the completed work in the first row, make a conjecture (statement) about what the second row of the chart will be. Justify your conjecture without computing the second row.
Answer:
Drawing 1 will be a reduction of Drawing 2. I know this because the corresponding lengths in Drawing 1 are smaller than the corresponding lengths in Drawing 2. Therefore, the scale factor from Drawing 2 to Drawing 1 would be less than 100%.
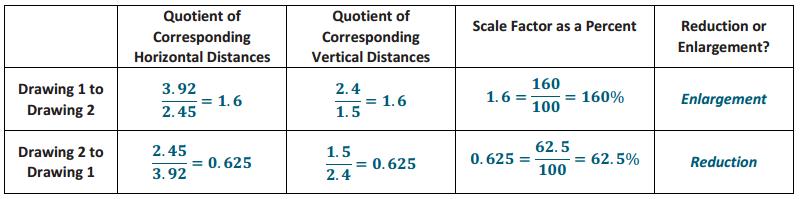
Compute the second row of the chart. Was your conjecture proven true? Explain how you know.
Answer:
The conjecture was true because the calculated scale factor from Drawing 2 to Drawing 1 was 62.5%. Since the scale factor is less than 100%, the scale drawing is indeed a reduction.
Eureka Math Grade 7 Module 4 Lesson 13 Problem Set Answer Key
Question 1.
The scale factor from Drawing 1 to Drawing 2 is 41 \(\frac{2}{3}\)%. Justify why Drawing 1 is a scale drawing of Drawing 2 and why it is an enlargement of Drawing 2. Include the scale factor in your justification.

Answer:
Quantity = Percent × Whole
Length in Drawing 1 = Percent × Length in Drawing 2
100% = Percent × 41 \(\frac{2}{3}\)%
\(\frac{100 \%}{41 \frac{2}{3} \%}\) = \(\frac{100 \cdot 3}{41 \frac{2}{3} \cdot 3}\) = \(\frac{300}{125}\) = \(\frac{12}{5}\) = 2.40 = 240%
Drawing 1 is a scale drawing of Drawing 2 because the lengths of Drawing 1 would be larger than the corresponding lengths of Drawing 2.
Since the scale factor is greater than 100%, the scale drawing is an enlargement of the original drawing.
Question 2.
The scale factor from Drawing 1 to Drawing 2 is 40%, and the scale factor from Drawing 2 to Drawing 3 is 37.5%. What is the scale factor from Drawing 1 to Drawing 3? Explain your reasoning, and check your answer using an example.

Answer:
To find the scale factor from Drawing 1 to 3, I needed to find 37.5% of 40%, so (0.375)(0.40) = 0.15. The scale factor from Drawing 1 to Drawing 3 would be 15%.
Check: Assume the length of Drawing 1 is 10. Then, using the scale factor for Drawing 2, the corresponding length of Drawing 2 would be 4. Then, applying the scale factor to Drawing 3, Drawing 3 would be 4(0.375) = 1.5. To go directly from Drawing 1 to Drawing 3, which was found to have a scale factor of 15%, then 10(0.15) = 1.5.
Question 3.
Traci took a photograph and printed it to be a size of 4 units by 4 units as indicated in the diagram. She wanted to enlarge the original photograph to a size of 5 units by 5 units and 10 units by 10 units.
a. Sketch the different sizes of photographs.

Answer:
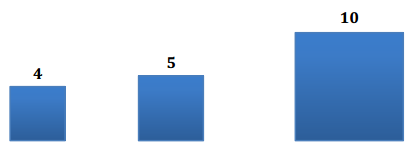
b. What was the scale factor from the original photo to the photo that is 5 units by 5 units?
Answer:
The scale factor from the original to the 5 by 5 enlargement is \(\frac{5}{4}\) = 1.25 = 125%.
c. What was the scale factor from the original photo to the photo that is 10 units by 10 units?
Answer:
The scale factor from the original to the 10 by 10 photo is \(\frac{10}{4}\) = 2.5 = 250%.
d. What was the scale factor from the 5 × 5 photo to the 10 × 10 photo?
The scale factor from the 5 × 5 photo to the 10 × 10 photo is \(\frac{10}{5}\) = 2 = 200%.
e. Write an equation to verify how the scale factor from the original photo to the enlarged 10 × 10 photo can be calculated using the scale factors from the original to the 5 × 5 and then from the 5 × 5 to the 10 × 10.
Answer:
Scale factor original to 5 × 5: (125%)
Scale factor 5 × 5 to 10 × 10: (200%)
4(1.25) = 5
5(2.00) = 10
Original to 10 × 10, scale factor = 250%
4(2.50) = 10
The true equation 4(1.25)(2.00) = 4(2.50) verifies that a single scale factor of 250% is equivalent to a scale factor of 125% followed by a scale factor of 200%.
Question 4.
The scale factor from Drawing 1 to Drawing 2 is 30%, and the scale factor from Drawing 1 to Drawing 3 is 175%. What are the scale factors of each given relationship? Then, answer the question that follows. Drawings are not to scale.
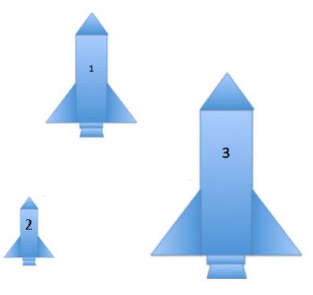
a. Drawing 2 to Drawing 3
Answer:
The scale factor from Drawing 2 to Drawing 3 is
\(\frac{175 \%}{30 \%}\) = \(\frac{1.75}{0.30}\) = \(\frac{175}{30}\) = \(\frac{35}{6}\) = 5 \(\frac{5}{6}\) = 583 \(\frac{1}{3}\)%.
b. Drawing 3 to Drawing 1
Answer:
The scale factor from Drawing 3 to Drawing 1 is
\(\frac{1}{1.75}\) = \(\frac{100}{175}\) = \(\frac{4}{7}\) ≈ 57.14%.
c. Drawing 3 to Drawing 2
Answer:
The scale factor from Drawing 3 to Drawing 2 is
\(\frac{0.3}{1.75}\) = \(\frac{30}{175}\) = \(\frac{6}{35}\) ≈ 17.14%.
d. How can you check your answers?
Answer:
To check my answers, I can work backwards and multiply the scale factor from Drawing 1 to Drawing 3 of 175% to the scale factor from Drawing 3 to Drawing 2, and I should get the scale factor from Drawing 1 to Drawing 2.
(1.75)(0.1714) ≈ 0.29995 ≈ 0.30 = 30%
Eureka Math Grade 7 Module 4 Lesson 13 Exit Ticket Answer Key
Question 1.
Compute the scale factor, as a percent, for each given relationship. When necessary, round your answer to the nearest tenth of a percent.
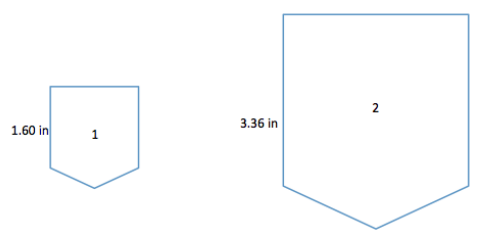
a. Drawing 1 to Drawing 2
Answer:
Drawing 2 = Percent × Drawing 1
3.36 = Percent × 1.60
\(\frac{3.36}{1.60}\) = 2.10 = 210%
b. Drawing 2 to Drawing 1
Answer:
Drawing 1 = Percent × Drawing 2
1.60 = Percent × 3.36
\(\frac{1.60}{3.36}\) = \(\frac{1}{2.10}\) ≈ 0.476190476 ≈ 47.6%
c. Write two different equations that illustrate how each scale factor relates to the lengths in the diagram.
Answer:
Drawing 1 to Drawing 2:
1.60(2.10) = 3.36
Drawing 2 to Drawing 1:
3.36(0.476) = 1.60
Question 2.
Drawings 2 and 3 are scale drawings of Drawing 1. The scale factor from Drawing 1 to Drawing 2 is 75%, and the scale factor from Drawing 2 to Drawing 3 is 50%. Find the scale factor from Drawing 1 to Drawing 3.
Answer:
Drawing 1 to 2 is 75%. Drawing 2 to 3 is 50%. Therefore, Drawing 3 is 50% of 75%, so
(0.50)(0.75) = 0.375. To determine the scale factor from Drawing 1 to Drawing 3, we went from 100% to 37.5%. Therefore, the scale factor is 37.5%. Using the relationship:
Drawing 3 = Percent × Drawing 1
37.5% = Percent × 100%
0.375 = Percent
= 37.5%