Engage NY Eureka Math 7th Grade Module 6 Lesson 19 Answer Key
Eureka Math Grade 7 Module 6 Lesson 19 Example Answer Key
Example 1.
If slices parallel to the tabletop (with height a whole number of units from the tabletop) were taken of this figure, then what would each slice look like?
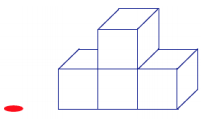
Answer:
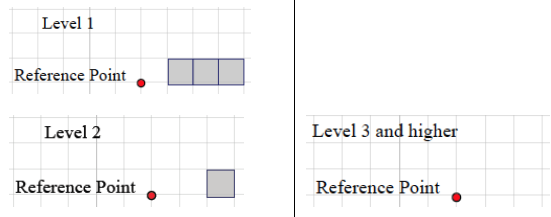
Example 2.
If slices parallel to the tabletop were taken of this figure, then what would each slice look like?
Answer:
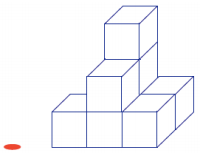
Example 3.
Given the level slices in the figure, how many unit cubes are in the figure?
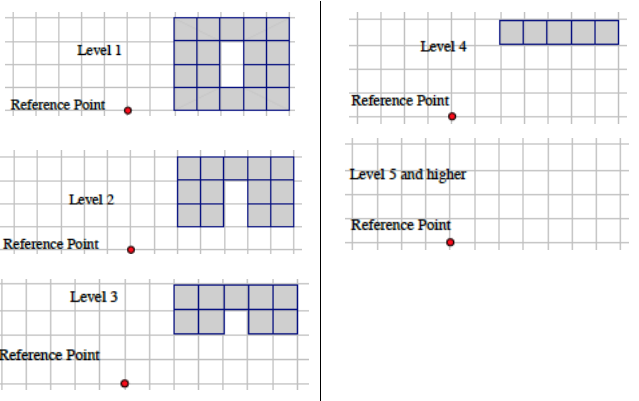
Answer:
The number of unit cubes can be determined by counting the shaded squares in Levels 1–4.
Level 1: There are 18 cubes between Level 0 and Level 1.
Level 2: There are 13 cubes between Level 1 and Level 2.
Level 3: There are 9 cubes between Level 2 and Level 3.
Level 4: There are 5 cubes between Level 3 and Level 4.
The total number of cubes in the solid is 45.
Eureka Math Grade 7 Module 6 Lesson 19 Exercise Answer Key
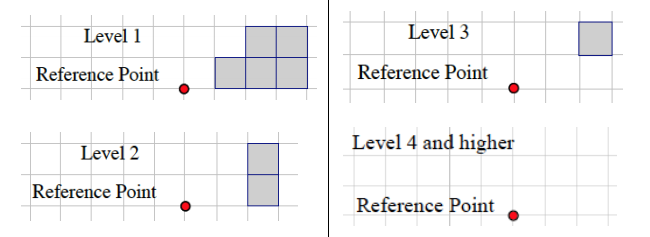
Exercise 1.
Based on the level slices you determined in Example 2, how many unit cubes are in the figure?
Answer:
The number of unit cubes can be determined by counting the shaded squares in Levels 1–3.
Level 1: Five shaded squares; there are 5 cubes between Level 0 and Level 1.
Level 2: Two shaded squares; there are 2 cubes between Level 1 and Level 2.
Level 3: One shaded square; there is 1 cube between Level 2 and Level 3.
The total number of cubes in the solid is 8.
Exercise 2.
a. If slices parallel to the tabletop were taken of this figure, then what would each slice look like?
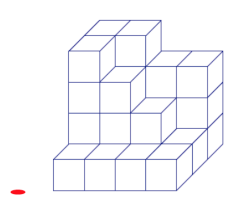
b. Given the level slices in the figure, how many unit cubes are in the figure?
Answer:
a.
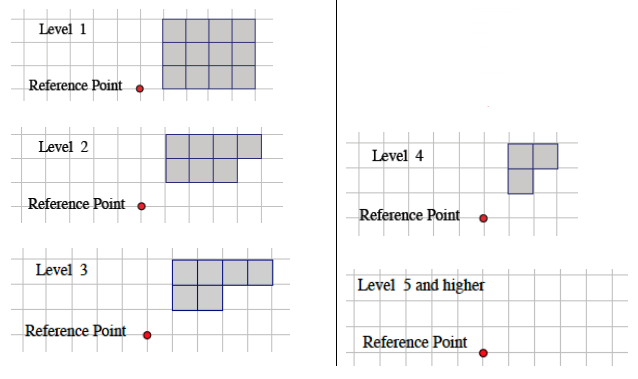
b. The number of unit cubes can be determined by counting the shaded squares in Levels 1–4.
Level 1: There are 12 cubes between Level 0 and Level 1.
Level 2: There are 7 cubes between Level 1 and Level 2.
Level 3: There are 6 cubes between Level 2 and Level 3.
Level 4: There are 3 cubes between Level 3 and Level 4.
The total number of cubes in the solid is 28.
Exercise 3.
Sketch your own three-dimensional figure made from cubes and the slices of your figure. Explain how the slices relate to the figure.
Answer:
Responses will vary.
Eureka Math Grade 7 Module 6 Lesson 19 Problem Set Answer Key
In the given three-dimensional figures, unit cubes are stacked exactly on top of each other on a tabletop. Each block is either visible or below a visible block.
Question 1.
a. The following three-dimensional figure is built on a tabletop. If slices parallel to the tabletop are taken of this figure, then what would each slice look like?
b. Given the level slices in the figure, how many cubes are in the figure?
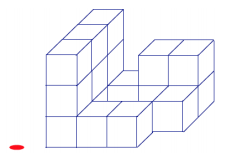
Answer:
a.
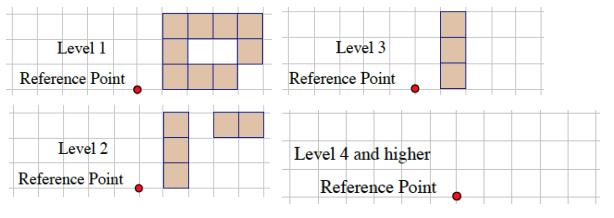
b. Given the level slices in the figure, how many cubes are in the figure?
The number of unit cubes can be determined by counting the shaded squares in Levels 1–3.
Level 1: There are 9 cubes between Level 0 and Level 1.
Level 2: There are 5 cubes between Level 1 and Level 2.
Level 3: There are 3 cubes between Level 2 and Level 3.
The total number of cubes in the solid is 17.
Question 2.
a. The following three-dimensional figure is built on a tabletop. If slices parallel to the tabletop are taken of this figure, then what would each slice look like?
b. Given the level slices in the figure, how many cubes are in the figure?
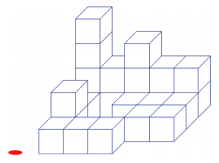
Answer:
a.
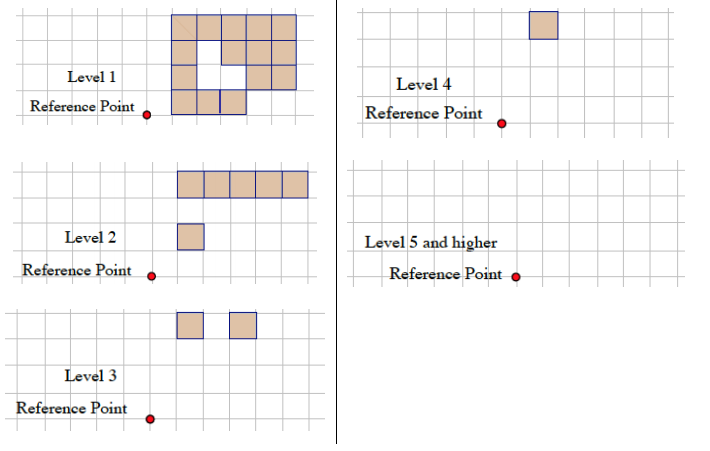
b. The number of unit cubes can be determined by counting the shaded squares in Levels 1–4.
Level 1: There are 15 cubes between Level 0 and Level 1.
Level 2: There are 6 cubes between Level 1 and Level 2.
Level 3: There are 2 cubes between Level 2 and Level 3.
Level 4: There is 1 cube between Level 3 and Level 4.
The total number of cubes in the solid is 24.
Question 3.
a. The following three-dimensional figure is built on a tabletop. If slices parallel to the tabletop are taken of this figure, then what would each slice look like?
b. Given the level slices in the figure, how many cubes are in the figure?
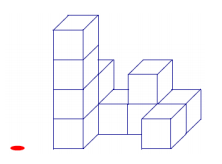
Answer:
a.
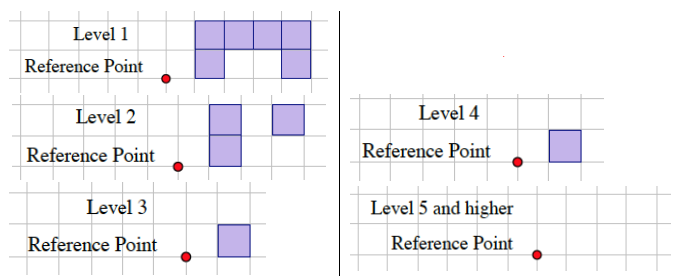
b. The number of unit cubes can be determined by counting the shaded squares in Levels 1–4.
Level 1: There are 6 cubes between Level 0 and Level 1.
Level 2: There are 3 cubes between Level 1 and Level 2.
Level 3: There is 1 cube between Level 2 and Level 3.
Level 4: There is 1 cube between Level 3 and Level 4.
The total number of cubes in the solid is 11.
Question 4.
John says that we should be including the Level 0 slice when mapping slices. Naya disagrees, saying it is correct to start counting cubes from the Level 1 slice. Who is right?
Answer:
Naya is right because the Level 0 slice and Level 1 slice are the tops and bottoms of the same set of cubes; counting cubes in both slices would be double counting cubes.
Question 5.
Draw a three-dimensional figure made from cubes so that each successive layer farther away from the tabletop has one less cube than the layer below it. Use a minimum of three layers. Then draw the slices, and explain the connection between the two.
Answer:
Responses will vary.
Eureka Math Grade 7 Module 6 Lesson 19 Exit Ticket Answer Key
Question 1.
The following three-dimensional figure is built on a tabletop. If slices parallel to the tabletop are taken of this figure, then what would each slice look like?
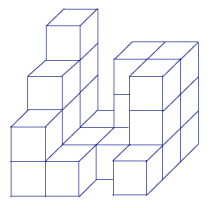
Answer:
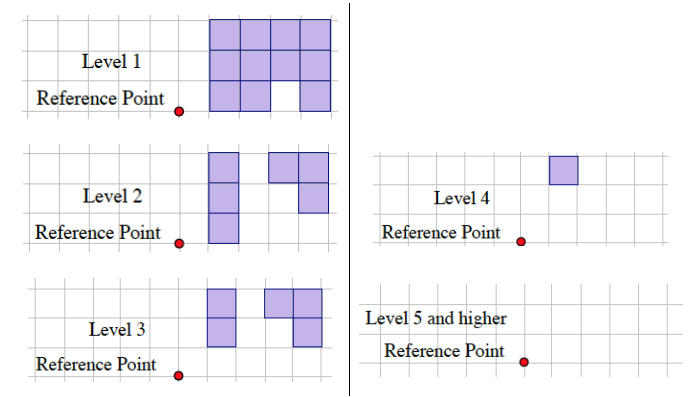
Question 2.
Given the level slices in the figure, how many cubes are in the figure?
Answer:
The number of unit cubes can be determined by counting the shaded squares in Levels 1–4.
Level 1: There are 11 cubes between Level 0 and Level 1.
Level 2: There are 6 cubes between Level 1 and Level 2.
Level 3: There are 5 cubes between Level 2 and Level 3.
Level 4: There is 1 cube between Level 3 and Level 4.
The total number of cubes in the solid is 23.