Eureka Math Grade 7 Module 6 Lesson 23 Answer Key

Engage NY Eureka Math 7th Grade Module 6 Lesson 23 Answer Key

Eureka Math Grade 7 Module 6 Lesson 23 Example Answer Key

Example 1.
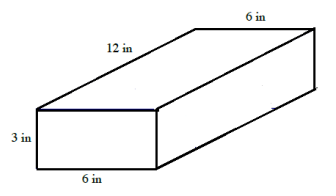
a. Calculate the surface area of the rectangular prism.

b. Imagine that a piece of the rectangular prism is removed. Determine the surface area of both pieces.

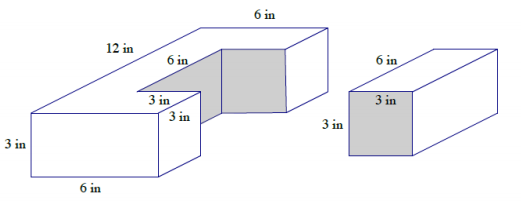
c. How is the surface area in part (a) related to the surface area in part (b)?
Answer:
a. Surface area:
2(3 in. × 6 in.) + 2(3 in. × 12 in.) + 2(6 in. × 12 in.)
= 2(18 in²) + 2(36 in²) + 2(72 in² )
= 36 in² + 72 in² + 144 in²
= 252 in²

b.
→ How did you determine the surface area of the shape on the left?
→ I was able to calculate the area of the sides that are rectangles using length times width. For the two bases that are C – shaped, I used the area of the original top and bottom and subtracted the piece that was taken off.

c. If I add the surface area of both figures, I will get more than the surface area of the original shape.
234 in² + 90 in² = 324 in²
324 in² – 252 in² = 72 in²
72 in² is twice the area of the region where the two pieces fit together.
There are 72 more square inches when the prisms are separated.

Eureka Math Grade 7 Module 6 Lesson 23 Exercise Answer Key

Opening Exercise
Calculate the surface area of the square pyramid.

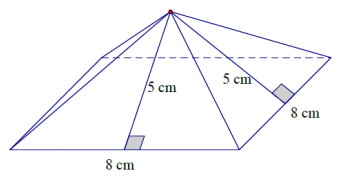
Answer:
Area of the square base:
s² = (8 cm)²
= 64 cm²
Area of the triangular lateral sides:
\(\frac{1}{2}\) bh = \(\frac{1}{2}\)(8 cm)(5 cm)
= 20 cm²
There are four lateral sides. So, the area of all 4 triangles is 80 cm².

Surface area:
(8 cm ∙ 8 cm) + 4(1/2 (8 cm ∙ 5 cm)) = 64 cm² + 80 cm² = 144 cm²

→ Explain the process you used to determine the surface area of the pyramid.
Answers will vary. I drew a net to determine the area of each side and added the areas together.

→ The surface area of a pyramid is the union of its base region and all its lateral faces.
→ Explain how (8 cm ∙ 8 cm) + 4(\(\frac{1}{2}\)(8 cm∙5 cm)) represents the surface area.
The area of the square with side lengths of 8 cm is represented by (8 cm ∙ 8 cm), and the area of the four lateral faces with base lengths of 8 cm and heights of 5 cm is represented by 4(\(\frac{1}{2}\) (8 cm∙5 cm)).

→ Would this method work for any prism or pyramid?
Answers will vary. Calculating the area of each face, including bases, will determine the surface area even if the areas are determined in different orders, by using a formula or net, or any other method.

Determine the surface area of the right prisms.
Exercise 1.

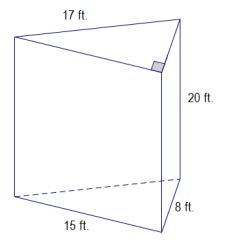
Answer:
Area of top and bottom: 2(\(\frac{1}{2}\)(15 ft.  × 8 ft.) )
= 15 ft. × 8 ft. = 120 ft²
Area of front: 15 ft. × 20 ft. = 300 ft²
Area that can be seen from left: 17 ft. × 20 ft. = 340 ft²
Area that can be seen from right: 8 ft. × 20 ft. = 160 ft²
Surface area: 120 ft² + 300 ft² + 340 ft² + 160 ft² = 920 ft²

Exercise 2.

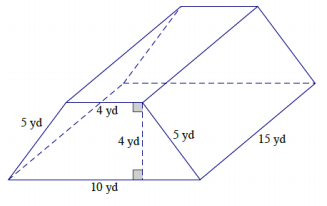
Answer:
Area of front and back: 2(\(\frac{1}{2}\)(10 yd. + 4 yd.)4 yd.)
= 14 yd. × 4 yd. = 56 yd²
Area of top: 4 yd. × 15 yd. = 60 yd²
Area that can be seen from left and right: 2(5 yd. × 15 yd.)
= 2(75 yd²) = 150 yd²
Area of bottom: 10 yd. × 15 yd. = 150 yd²
Surface area: 56 yd² + 60 yd² + 150 yd² + 150 yd² = 416 yd²

Exercise 3.

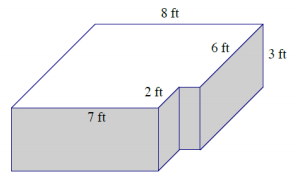
Answer:
Area of top and bottom: 2((8 ft. × 6 ft.) + (7 ft. × 2 ft.))
= 2(48 ft² + 14 ft² )
= 2(62 ft² ) = 124 ft²
Area for back: 8 ft. × 3 ft. = 24 ft²

Area for front: 7 ft. × 3 ft. = 21 ft²

Area of corner cutout: (2 ft. × 3 ft.) + (1 ft. × 3 ft.) = 9 ft²
Area of right side: 6 ft. × 3 ft. = 18 ft²
Area of left side: 8 ft. × 3 ft. = 24 ft²

Surface area: 124 ft² + 24 ft² + 21 ft² + 9 ft² + 18 ft² + 24 ft² = 220 ft²

Exercise 4.

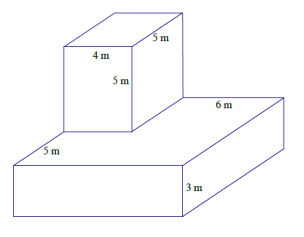
Answer:
Surface area of top prism:
Area of top: 4 m × 5 m = 20 m²
Area of front and back sides: 2(4 m × 5 m) = 40 m²
Area of left and right sides: 2(5 m × 5 m) = 50 m²
Total surface area of top prism: 20 m² + 40 m² + 50 m² = 110 m²
Surface area of bottom prism:
Area of top: 10 m × 10 m – 20 m² = 80 m²
Area of bottom: 10 m × 10 m = 100 m²
Area of front and back sides: 2(10 m × 3 m) = 60 m²
Area of left and right sides: 2(10 m × 3 m) = 60 m²
Total surface area of bottom prism: 80 m² + 100 m² + 60 m² + 60 m²
= 300 m²

Surface area: 110 m² + 300 m² = 410 m²

Exercise 5.

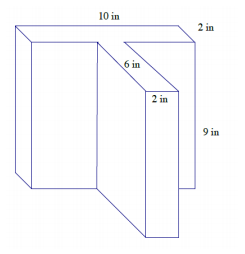
Answer:
Area of top and bottom faces: 2(10 in. × 2 in.) + 2(6 in. × 2 in.)
= 40 in² + 24 in²
= 64 in²
Area of lateral faces: 2(9 in. × 2 in.) + 2(6 in. × 9 in.) + 2(9 in. × 10 in.)
= 36 in² + 108 in² + 180 in²
= 324 in²
Surface area:
64 in² + 324 in² = 388 in²

Eureka Math Grade 7 Module 6 Lesson 23 Problem Set Answer Key

Determine the surface area of the figures.
Question 1.

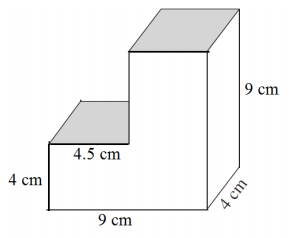
Answer:
Area of top and bottom: 2(9 cm × 4 cm) = 72 cm²
Area of left and right sides: 2(4 cm × 9 cm) = 72 cm²
Area of front and back: 2(9 cm × 4 cm) + 2(4.5 cm × 5 cm)
= 117 cm²
Surface area: 72 cm² + 72 cm² + 117 cm² = 261 cm²

Question 2.

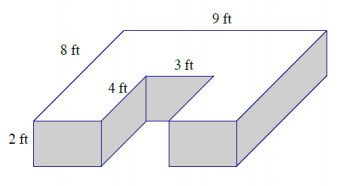
Answer:
Area of front and back: 2(9 ft. × 2 ft.) = 36 ft²

Area of sides: 2(8 ft. × 2 ft.) = 32 ft²

Area of top and bottom: 2(9 ft. × 8 ft.) – 2(4 ft. × 3 ft.)
= 144 ft² – 24 ft²
= 120 ft²
Area of interior sides: 2(4 ft. × 2 ft.) = 16 ft²
Surface area: 36 ft² + 32 ft² + 120 ft² + 16 ft² = 204 ft²

Question 3.

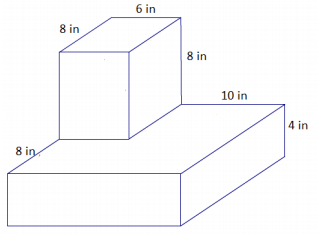
Answer:
Surface area of top prism:
Area of top: 8 in. × 6 in. = 48 in²
Area of front and back sides: 2(6 in. × 8 in.) = 96 in²
Area of left and right sides: 2(8 in. × 8 in.) = 128 in²
Total surface area of top prism: 48 in² + 96 in² + 128 in² = 272 in²
Surface area of bottom prism:
Area of top: 16 in. × 16 in. – 48 in² = 208 in²
Area of bottom: 16 in. × 16 in. = 256 in²
Area of front and back sides: 2(16 in. × 4 in.) = 128 in²
Area of left and right sides: 2(16 in. × 4 in.) = 128 in²
Total surface area of bottom prism: 208 in² + 256 in² + 128 in² + 128 in²
= 720 in²

Surface area: 272 in² + 720 in² = 992 in²

Question 4.

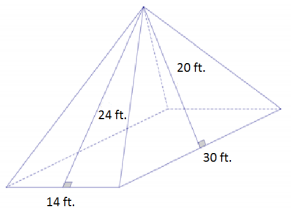
Answer:
Area of the rectangle base: 14 ft. × 30 ft. = 420 ft²
Area of the triangular lateral sides:
Area of front and back: \(\frac{1}{2}\)bh
= 2(\(\frac{1}{2}\)(14 ft.)(24 ft.))
= 336 ft²

Area that can be seen from left and right: \(\frac{1}{2}\)bh
= 2(1\(\frac{1}{2}\)(30 ft.)(20 ft.))
= 600 ft²
Surface area: 420 ft² + 336 ft² + 600 ft² = 1,356 ft²

Question 5.

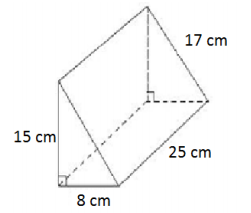
Answer:
Area of front and back: 2(\(\frac{1}{2}\)(8 cm × 15 cm))
= 8 cm × 15 cm
= 120 cm²
Area of bottom: 8 cm × 25 cm
= 200 cm²
Area that can be seen from left side: 25 cm × 15 cm
= 375 cm²
Area that can be seen from right side: 25 cm × 17 cm
= 425 cm²

Surface area: 120 cm² + 200 cm² + 375 cm² + 425 cm² = 1,120 cm²

Eureka Math Grade 7 Module 6 Lesson 23 Exit Ticket Answer Key

Determine and explain how to find the surface area of the following right prisms.
Question 1.

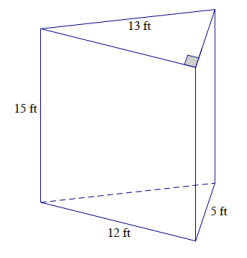
Answer:
Area of top and bottom: 2(\(\frac{1}{2}\)(12 ft. × 5 ft.))
= 12 ft. × 5 ft.
= 60 ft²
Area of front: 12 ft. × 15 ft.
= 180 ft²
Area seen from left: 13 ft. × 15 ft.
= 195 ft²
Area seen from right: 5 ft. × 15 ft.
= 75 ft²
Surface area: 60 ft² + 180 ft² + 195 ft² + 75 ft²
= 510 ft²
To find the surface area of the triangular prism, I must sum the areas of two triangles (the bases that are equal in area) and the areas of three different – sized rectangles.

Question 2.

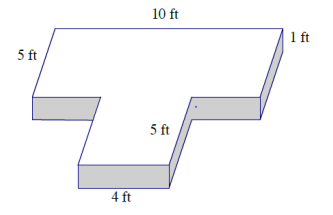
Answer:
Area of front and back: 2(10 ft. × 1 ft.) = 20 ft²
Area of sides: 2(10 ft. × 1 ft.) = 20 ft²
Area of top and bottom: 2(10 ft. × 5 ft.) + 2(4 ft. × 5 ft.)
= 100 ft² + 40 ft²
= 140 ft²
Surface area: 20 ft² + 20 ft² + 140 ft²
= 180 ft²
To find the surface area of the prism, I must sum the composite area of the bases with rectangular areas of the sides of the prism.