Engage NY Eureka Math 7th Grade Module 6 Lesson 26 Answer Key
Eureka Math Grade 7 Module 6 Lesson 26 Example Answer Key
Example 1.
Find the volume of the following three – dimensional object composed of two right rectangular prisms.
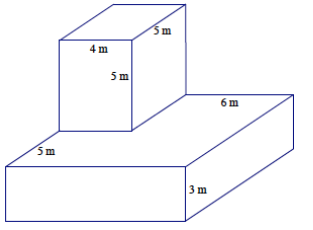
Answer:
Volume of object = Volume of top prism + Volume of bottom prism
Volume of top prism: Volume of bottom prism:
Volumetop prism = (4 m)(5 m)(5 m)
= 100 m3
Volumebottom prism = (10 m)(10 m)(3 m)
= 300 m3
The volume of the object is 100 m3 + 300 m3 = 400 m3.
There are different ways the volume of a composite figure may be calculated. If the figure is like the one shown in Example 1, where the figure can be decomposed into separate prisms and it would be impossible for the prisms to share any one dimension, the individual volumes of the decomposed prisms can be determined and then summed. If, however, the figure is similar to the figure in Exercise 1, there are two possible strategies. In Exercise 1, the figure can be decomposed into two individual prisms, but a dimension is shared between the two prisms—in this case, the height. Instead of calculating the volume of each prism and then taking the sum, we can calculate the area of the entire base by decomposing it into shapes we know and then multiplying the area of the base by the height.
Example 2.
Find the volume of the right prism shown in the diagram whose base is the region between two right triangles. Use two different strategies.
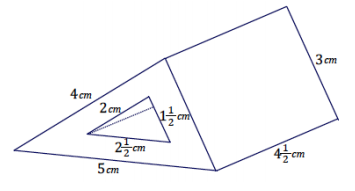
Answer:
Strategy 1
The volume of the right prism is equal to the difference of the volumes of the two triangular prisms.
Volume of object = Volumelarge prism – Volumesmall prism
Volume of large prism:
Volumelarge prism = (\(\frac{1}{2}\) ∙ 3 cm ∙ 4 cm)4 \(\frac{1}{2}\)cm
= 27 cm3
Volume of small prism:
Volumesmall prism = (\(\frac{1}{2}\) ∙ 1 \(\frac{1}{2}\)cm ∙ 2 cm) 4\(\frac{1}{2}\)cm
= 6 \(\frac{3}{4}\)cm3
The volume of the object is 20 \(\frac{1}{4}\)cm3.
Strategy 2
The volume of a right prism is equal to the area of its base times its height. The base is the region between two right triangles.
Volume of object = Bh
B = Arealarge triangle – Areasmall triangle
Arealarge triangle = \(\frac{1}{2}\) ∙ 3 cm ∙ 4 cm = 6 cm2
Areasmall triangle = \(\frac{1}{2}\) ∙ 1 1\(\frac{1}{2}\)cm ∙ 2 cm = 1 \(\frac{1}{2}\)cm2
B = 6 cm2 – 1 \(\frac{1}{2}\)cm2 = 4 \(\frac{1}{2}\)cm2
Volume of object:
Volumeobject = Bh
= (4 \(\frac{1}{2}\)cm2 ∙ 4 \(\frac{1}{2}\)cm)
= 20 \(\frac{1}{4}\)cm3
The volume of the object is 20 \(\frac{1}{4}\)cm3.
→ Write a numeric expression to represent the volume of the figure in Strategy 1.
(\(\frac{1}{2}\) ∙ 3 cm ∙ 4 cm)4 \(\frac{1}{2}\)cm – (\(\frac{1}{2}\) ∙ 1 \(\frac{1}{2}\)cm ∙ 2 cm)4 \(\frac{1}{2}\)cm
→ Write a numeric expression to represent the volume of the figure in Strategy 2.
4 \(\frac{1}{2}\)cm
→ How do the numeric expressions represent the problem differently?
The first expression is appropriate to use when the volume of the smaller prism is being subtracted away from the volume of the larger prism, whereas the second expression is used when the area of the base of the composite figure is found and then multiplied by the height to determine the volume.
→ What property allows us to show that these representations are equivalent?
The distributive property
Example 3.
A box with a length of 2 ft., a width of 1.5 ft., and a height of 1.25 ft. contains fragile electronic equipment that is packed inside a larger box with three inches of styrofoam cushioning material on each side (above, below, left side, right side, front, and back).
a. Give the dimensions of the larger box.
b. Design styrofoam right rectangular prisms that could be placed around the box to provide the cushioning (i.e., give the dimensions and how many of each size are needed).
c. Find the volume of the styrofoam cushioning material by adding the volumes of the right rectangular prisms in the previous question.
d. Find the volume of the styrofoam cushioning material by computing the difference between the volume of the larger box and the volume of the smaller box.
Answer:
a. Length 2.5 ft., width 2 ft., and height 1.75 ft.
b. Possible answer: Two pieces with dimensions 2.5 ft. ∙ 2 ft. ∙ 3 in. and four pieces with dimensions 2 ft. ∙ 1.25 ft. ∙ 3 in.
c. V1 = 2(2.5 ft. ∙ 2 ft. ∙ 0.25 ft.) = 2.5 ft3
V2 = 4(2 ft. ∙ 1.25 ft. ∙ 0.25 ft.) = 2.5 ft3
V1 + V2 = 2.5 ft3 + 2.5 ft3 = 5 ft3
d. (2.5 ft. ∙ 2 ft. ∙ 1.75 ft.) – (2 ft. ∙ 1.5 ft. ∙ 1.25 ft.) = 8.75 ft3 – 3.75 ft3 = 5 ft3
Eureka Math Grade 7 Module 6 Lesson 26 Exercise Answer Key
Exercise 1.
Find the volume of the following three – dimensional figure composed of two right rectangular prisms.
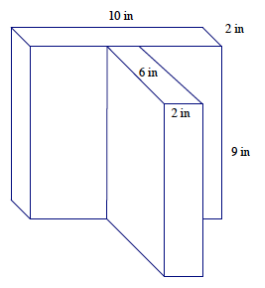
Answer:
Area of Baseback prism = (2 in.)( 10 in.)
= 20 in.2
Area of Basefront prism = (6 in.)(2 in.)
= 12 in2
Area of Base = 20 in2 + 12 in2 = 32 in2
The volume of the object is (9 in.)(32 in2 ) = 288 in3.
Exercise 2.
The right trapezoidal prism is composed of a right rectangular prism joined with a right triangular prism. Find the volume of the right trapezoidal prism shown in the diagram using two different strategies.
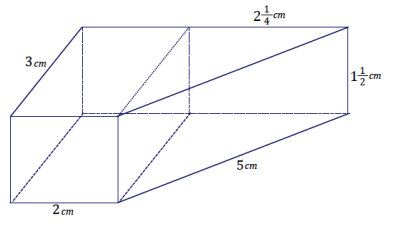
Answer:
Strategy 1
The volume of the trapezoidal prism is equal to the sum of the volumes of the rectangular and triangular prisms.
Volume of object = Volume of rectangular prism + Volume of triangular prism
Volume of rectangular prism: Volume of triangular prism:
Volumerectangular prism = Bh
= (lw)h
= (3 cm ∙ 2 cm) ∙ 1 \(\frac{1}{2}\)cm
= 9 cm3
Volumetriangular prism = Bh = (\(\frac{1}{2}\) lw)h
= (\(\frac{1}{2}\) ∙ 3 cm ∙ 2\(\frac{1}{4}\)cm) ∙ 1 \(\frac{1}{2}\)cm
= 5 \(\frac{1}{16}\) cm3
The volume of the object is 9 cm3 + 5 \(\frac{1}{16}\) cm3 = 14 \(\frac{1}{16}\) cm3.
Strategy 2
The volume of a right prism is equal to the area of its base times its height. The base consists of a rectangle and a triangle.
Volume of object = Bh
B = Arearectangle + Areatriangle
Arearectangle = 3 cm ∙ 2 cm = 6 cm2
Areatriangle = \(\frac{1}{2}\) ∙ 3 cm ∙ 2 \(\frac{1}{4}\)cm = 3 \(\frac{3}{8}\)cm2
B = 6 cm2 + 3 \(\frac{3}{8}\)cm2 = 9 \(\frac{3}{8}\)cm2
Volume of object:
Volumeobject = Bh
= (9 \(\frac{3}{8}\)cm2 )(1\(\frac{1}{2}\)cm)
= 14 \(\frac{1}{16}\)cm3
The volume of the object is 14\(\frac{1}{16}\)cm3.
→ Write a numeric expression to represent the volume of the figure in Strategy 1.
(3 cm ∙ 2 cm) ∙ 1 \(\frac{1}{2}\)cm + (\(\frac{1}{2}\) ∙ 3 cm ∙ 2 \(\frac{1}{4}\)cm) ∙ 1 \(\frac{1}{2}\)cm
→ Write a numeric expression to represent the volume of the figure in Strategy 2.
(3 cm ∙ 2 cm + \(\frac{1}{2}\) ∙ 3 cm ∙ 2 \(\frac{1}{4}\)cm )(1 \(\frac{1}{2}\)cm)
→ How do the numeric expressions represent the problem differently?
The first expression is appropriate to use when individual volumes of the decomposed figure are being added together, whereas the second expression is used when the area of the base of the composite figure is found and then multiplied by the height to determine the volume.
→ What property allows us to show that these representations are equivalent?
The distributive property.
Eureka Math Grade 7 Module 6 Lesson 26 Problem Set Answer Key
Question 1.
Find the volume of the three – dimensional object composed of right rectangular prisms.
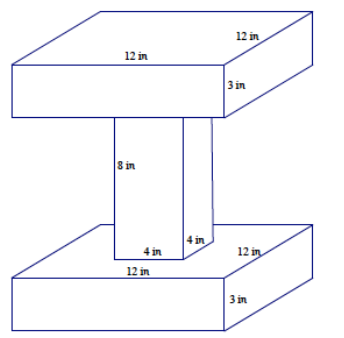
Answer:
Volumeobject = Volumetop and bottom prisms + Volumemiddle prism
Volume of top and bottom prisms:
V = 2(12 in. ∙ 12 in. ∙ 3 in.)
= 864 in3
Volume of middle prism:
= 4 in. ∙ 4 in. ∙ 8 in.
= 128 in3
The volume of the object is 864 in3 + 128 in3 = 992 in3.
Question 2.
A smaller cube is stacked on top of a larger cube. An edge of the smaller cube measures \(\frac{1}{2}\) cm in length, while the larger cube has an edge length three times as long. What is the total volume of the object?
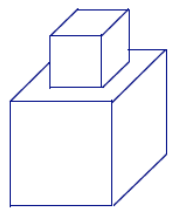
Answer:
Volumeobject = Volumesmall cube + Volumelarge cube
Volumesmall cube = (\(\frac{1}{2}\) cm)3
= \(\frac{1}{8}\) cm3
Volumelarge cube = (\(\frac{3}{2}\) cm)3
= \(\frac{27}{8}\) cm3
V = \(\frac{1}{8}\) cm3 + \(\frac{27}{8}\) cm3
= 3 \(\frac{1}{2}\) cm3
The total volume of the object is 3\(\frac{1}{2}\) cm3.
Question 3.
Two students are finding the volume of a prism with a rhombus base but are provided different information regarding the prism. One student receives Figure 1, while the other receives Figure 2.
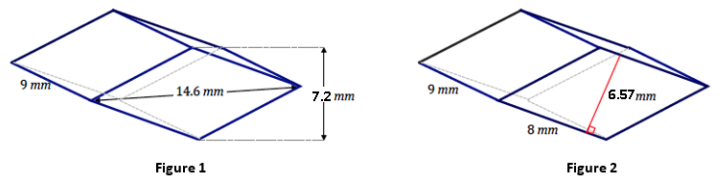
a. Find the expression that represents the volume in each case; show that the volumes are equal.
b. How does each calculation differ in the context of how the prism is viewed?
Answer:
a. Figure 1
2(\(\frac{1}{2}\) ∙ 14.6 mm ∙ 3.6 mm) ∙ 9 mm
473.04 mm3
Figure 2
((8 mm ∙ 6.57 mm) ∙ 9 mm)
473.04 mm3
b. In Figure 1, the prism is treated as two triangular prisms joined together. The volume of each triangular prism is found and then doubled, whereas in Figure 2, the prism has a base in the shape of a rhombus, and the volume is found by calculating the area of the rhomboid base and then multiplying by the height.
Question 4.
Find the volume of wood needed to construct the following side table composed of right rectangular prisms.
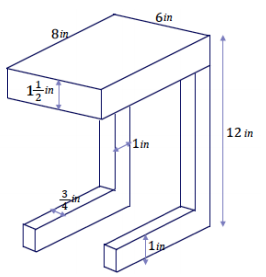
Answer:
Volume of bottom legs: V = 2(8 in. ∙ 1 in. ∙ 0.75 in.)
= 12 in3
Volume of vertical legs: V = 2(1 in. ∙ 9.5 in. ∙ 0.75 in.)
= 14.25 in3
Volume of tabletop: V = 8 in. ∙ 6 in. ∙ 1.5 in.
= 72 in3
The volume of the table is
12 in3 + 14.25 in3 + 72 in3 = 98.25 in3.
Question 5.
A plastic die (singular for dice) for a game has an edge length of 1.5 cm. Each face of the cube has the number of cubic cutouts as its marker is supposed to indicate (i.e., the face marked 3 has 3 cutouts). What is the volume of the die?
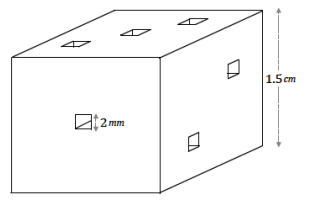
Answer:
Number of cubic cutouts:
1 + 2 + 3 + 4 + 5 + 6 = 21
Volume of cutout cubes: Volume of large cube:
V = 21(2 mm)3
V = 168 mm3 = 0.168 cm3 V = (1.5 cm)3
V = 3.375 cm3
The total volume of the die is
3.375 cm3 – 0.168 cm3 = 3.207 cm3.
Question 6.
A wooden cube with an edge length of 6 inches has square holes (holes in the shape of right rectangular prisms) cut through the centers of each of the three sides as shown in the figure. Find the volume of the resulting solid if the square for the holes has an edge length of 1 inch.
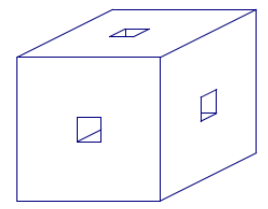
Answer:
Think of making the square holes between opposite sides by cutting three times: The first cut removes 6 in3, and the second and third cuts each remove 5 in3. The resulting solid has a volume of (6 in.)3 – 6 in3 – 5 in3 – 5 in3 = 200 in3.
Question 7.
A right rectangular prism has each of its dimensions (length, width, and height) increased by 50%. By what percent is its volume increased?
Answer:
V = l ∙ w ∙ h
V’ = 1.5l ∙ 1.5w ∙ 1.5h
V’ = 3.375lwh
The larger volume is 337.5% of the smaller volume. The volume has increased by 237.5%.
Question 8.
A solid is created by putting together right rectangular prisms. If each of the side lengths is increase by 40%, by what percent is the volume increased?
Answer:
If each of the side lengths is increased by 40%, then the volume of each right rectangular prism is multiplied by 1.43 = 2.744. Since this is true for each right rectangular prism, the volume of the larger solid, V’, can be found by multiplying the volume of the smaller solid, V, by 2.744 = 274.4% (i.e., V’ = 2.744V). This is an increase of 174.4%.
Eureka Math Grade 7 Module 6 Lesson 26 Exit Ticket Answer Key
Question 1.
A triangular prism has a rectangular prism cut out of it from one base to the opposite base, as shown in the figure. Determine the volume of the figure, provided all dimensions are in millimeters.
Is there any other way to determine the volume of the figure? If so, please explain.
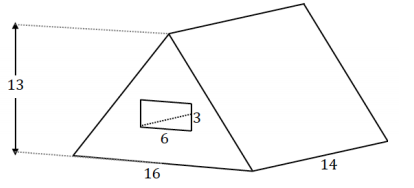
Answer:
Possible response:
Volume of the triangular prism: (\(\frac{1}{2}\) ∙ 16 mm ∙ 13 mm)(14 mm) = 1,456 mm3
Volume of the rectangular prism: (6 mm ∙ 3 mm ∙ 14 mm) = 252 mm3
Volume of the composite prism: 1,456 mm3 – 252 mm3 = 1,204 mm3
The calculations above subtract the volume of the cutout prism from the volume of the main prism. Another strategy would be to find the area of the base of the figure, which is the area of the triangle less the area of the rectangle, and then multiply by the height to find the volume of the prism.