Engage NY Eureka Math 8th Grade Module 1 Lesson 4 Answer Key
Eureka Math Grade 8 Module 1 Lesson 4 Exercise Answer Key
Exercise 1.
List all possible cases of whole numbers m and n for identity (1). More precisely, when m>0 and n>0, we already know that (1) is correct. What are the other possible cases of m and n for which (1) is yet to be verified?
Answer:
Case (A): m>0 and n=0
Case (B): m=0 and n>0
Case (C): m=n=0
Model how to check the validity of a statement using Case (A) with equation (1) as part of Exercise 2. Have students work independently or in pairs to check the validity of (1) in Case (B) and Case (C) to complete Exercise 2. Next, have students check the validity of equations (2) and (3) using Cases (A)–(C) for Exercises 3 and 4.
Exercise 2.
Check that equation (1) is correct for each of the cases listed in Exercise 1.
Answer:
Case (A): xm∙x0=xm? Yes, because xm∙x0=xm∙1=xm.
Case (B): x0∙xn=xn? Yes, because x0∙xn=1∙xn=xn.
Case (C): x0∙x0=x0? Yes, because x0∙x0=1∙1=x0.
Exercise 3.
Do the same with equation (2) by checking it case-by-case.
Answer:
Case (A): (xm)0=x0×m? Yes, because xm is a number, and a number raised to a zero power is 1. 1=x0=x0×m.
S0, the left side is 1. The right side is also 1 because x0×m=x0=1.
Case (B): (x0)n=xn×0? Yes, because, by definition x0=1 and 1n=1, the left side is equal to 1. The right side is equal to x0=1, so both sides are equal.
Case (C): (x0)0=x0×0? Yes, because, by definition of the zeroth power of x, both sides are equal to 1.
Exercise 4.
Do the same with equation (3) by checking it case-by-case.
Answer:
Case (A): (xy)0=x0 y0? Yes, because the left side is 1 by the definiti0n of the zeroth power, while the right side is
1×1=1.
Case (B): Since n>0, we already know that (3) is valid.
Case (C): This is the same as Case (A), which we have already shown to be valid.
Exercise 5.
Write the expanded form of 8,374 using exponential notation.
Answer:
8374=(8×103)+(3×102)+(7×101)+(4×100)
Exercise 6.
Write the expanded form of 6,985,062 using exponential notation.
Answer:
6 985 062
= (6×106)+(9×105)+(8×104)+(5×103)+(0×102)+(6×101) + (2×100)
Eureka Math Grade 8 Module 1 Lesson 4 Problem Set Answer Key
Let x,y be numbers (x,y≠0). Simplify each of the following expressions.
Question 1.
\(\frac{y^{12}}{y^{12}}\) = y12-12
Answer:
=y0
=1
Question 2.
915\(\frac{1}{9^{15}}\) = \(\frac{9^{15}}{9^{15}}\)
Answer:
=915-15
=90
=1
Question 3.
(7(123456.789)4)0=
Answer:
=70 (123456.789)4×0
=70 (123456.789)0
=1
Question 4.
22∙\(\frac{1}{2^{5}}\)∙25∙\(\frac{1}{2^{2}}\) =\(\frac{2^{2}}{2^{2}}\)∙\(\frac{2^{5}}{2^{5}}\)
Answer:
=22-2∙25-5
=20∙20
=1
Question 5.
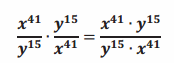
Answer:
= \(\frac{x^{41}}{x^{41}}\)∙\(\frac{y^{15}}{y^{15}}\)
= x41-41∙y15-15
=x0∙y0
= 1
Eureka Math Grade 8 Module 1 Lesson 4 Exit Ticket Answer Key
Question 1.
Simplify the following expression as much as posiible.
Answer:
\(\frac{4^{10}}{4^{10}}\).70 = 410-10.1 = 40.1 = 1.1 = 1
Question 2.
Let a and b be two numbers. Use the distributive law and then the definition of zeroth power to show that the numbers (a0+b0) a0 and (a0+b0) b0 are equal.
Answer:
(a0+b0) a0=a0∙a0+b0∙a0
=a0+0+a0 b0
=a0+a0 b0
=1+1∙1
=1+1
=2
(a0+b0) b0=a0∙b0+b0∙b0
=a0 b0+b0+0
=a0 b0+b0
=1∙1+1
=1+1
=2
Since both numbers are equal to 2, they are equal.
Eureka Math Grade 8 Module 1 Lesson 4 Sprint Answer Key
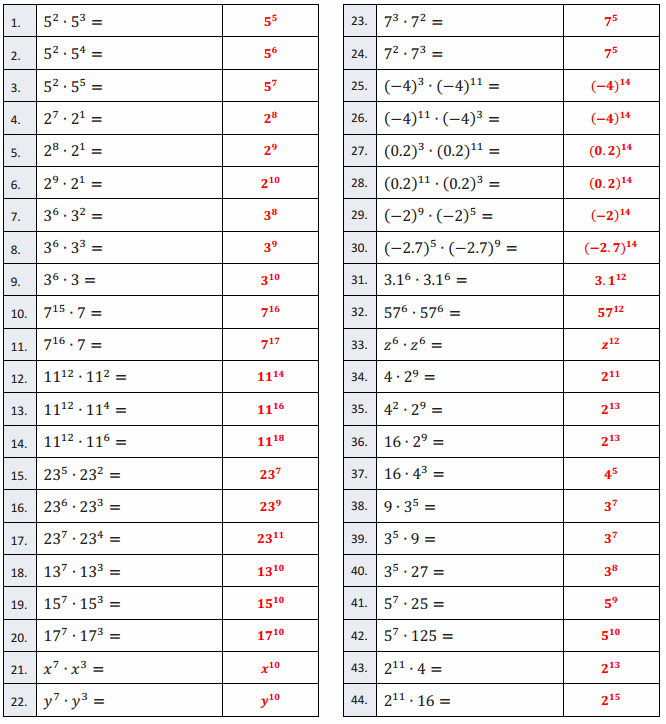
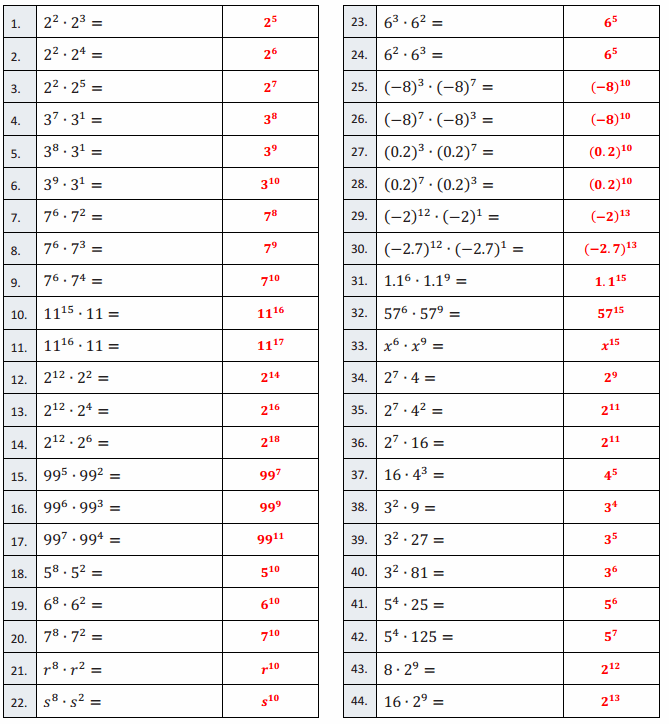
Applying Properties of Exponents to Generate Equivalent Expressions—Round 1
Directions: Simplify each expression using the laws of exponents. Use the least number of bases possible and only positive exponents. All letters denote numbers.

Answer:
Applying Properties of Exponents to Generate Equivalent Expressions—Round 2
Directions: Simplify each expression using the laws of exponents. Use the least number of bases possible and only positive exponents. All letters denote numbers.
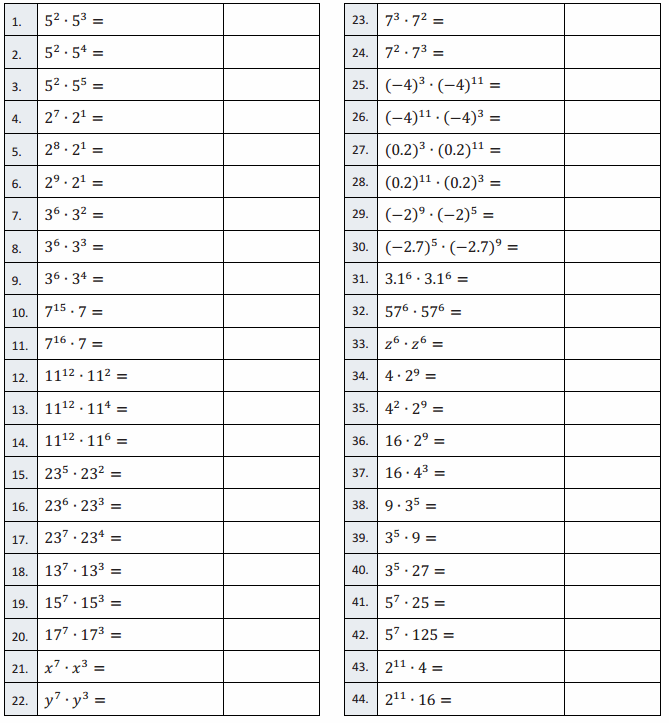
Answer: