Engage NY Eureka Math 8th Grade Module 3 Lesson 1 Answer Key
Eureka Math Grade 8 Module 3 Lesson 1 Exploratory Challenge Answer Key
Exploratory Challenge.
Two geometric figures are said to be similar if they have the same shape but not necessarily the same size. Using that informal definition, are the following pairs of figures similar to one another? Explain.
Pair A:
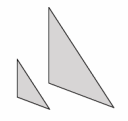
Answer:
Yes, these figures appear to be similar. They are the same shape, but one is larger than the other, or one is smaller than the other.
Pair B:
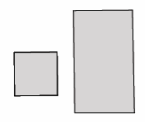
Answer:
No, these figures do not appear to be similar. One looks like a square and the other like a rectangle.
Pair C:
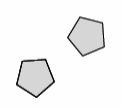
Answer:
These figures appear to be exactly the same, which means they are congruent.
Pair D:
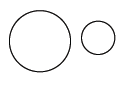
Answer:
Yes, these figures appear to be similar. They are both circles, but they are different sizes.
Pair E:
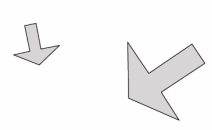
Answer:
Yes, these figures appear to be similar. They are the same shape, but they are different in size.
Pair F:

Answer:
Yes, these figures appear to be similar. The faces look the same, but they are just different in size.
Pair G:
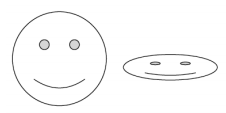
Answer:
They do not look to be similar, but I’m not sure. They are both happy faces, but one is squished compared to the other.
P air H:

Answer:
No, these two figures do not look to be similar. Each is curved but shaped differently.
Eureka Math Grade 8 Module 3 Lesson 1 Exercise Answer Key
Question 1.
Given |OP|=5 in.
a. If segment OP is dilated by a scale factor r=4, what is the length of segment OP’?
Answer:
|OP |=20 in. because the scale factor multiplied by the length of the original segment is 20; that is,
4 ∙ 5=20.
b. If segment OP is dilated by a scale factor r=\(\frac{1}{2}\), what is the length of segment OP’?
Answer:
|OP’ |=2.5 in. because the scale factor multiplied by the length of the original segment is 2.5; that is,
(\(\frac{1}{2}\))∙5=2.5.
Use the diagram below to answer Exercises 2–6. Let there be a dilation from center O. Then, Dilation(P)=P’ and Dilation(Q)=Q’. In the diagram below, |OP|=3 cm and |OQ|=4 cm, as shown.
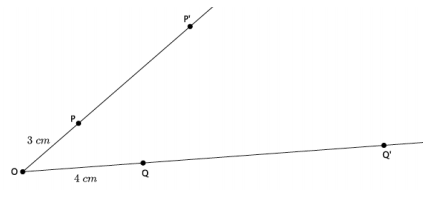
Question 2.
If the scale factor is r=3, what is the length of segment OP’?
Answer:
The length of the segment OP’ is 9 cm.
Question 3.
Use the definition of dilation to show that your answer to Exercise 2 is correct.
Answer:
|OP’ |=r |OP|; therefore, |OP’|=3∙3 cm=9 cm.
Question 4.
If the scale factor is r=3, what is the length of segment OQ’?
Answer:
The length of the segment OQ’ is 12 cm.
Question 5.
Use the definition of dilation to show that your answer to Exercise 4 is correct.
Answer:
|OQ’ |=r|OQ|; therefore, |OQ’ |=3∙4 cm=12 cm.
Question 6.
If you know that |OP|=3, |OP’ |=9, how could you use that information to determine the scale factor?
Answer:
Since we know |OP’|=r|OP|, we can solve for r: \(\frac{\left|o P^{\prime}\right|}{|O P|}\) =r, which is \(\frac{9}{3}\)=r or 3=r.
Eureka Math Grade 8 Module 3 Lesson 1 Exit Ticket Answer Key
Question 1.
Why do we need a better definition for similarity than “same shape, not the same size”?
Answer:
We need a better definition that includes dilation and a scale factor because some figures may look to be similar (e.g., the smiley faces), but we cannot know for sure unless we can check the proportionality. Other figures (e.g., the parabolas) may not look similar but are. We need a definition so that we are not just guessing if they are similar by looking at them.
Question 2.
Use the diagram below. Let there be a dilation from center O with scale factor 3. Then, Dilation(P)=P’. In the diagram below, |OP|=5 cm. What is |OP’ |? Show your work.
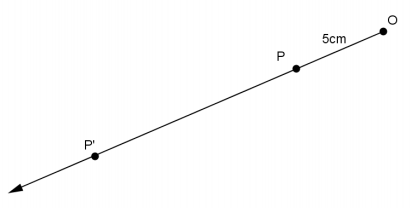
Answer:
Since |OP’|=r|OP|, then
|OP’|=3∙5 cm,
|OP’|=15 cm.
Question 3.
Use the diagram below. Let there be a dilation from center O. Then, Dilation(P)=P’. In the diagram below, |OP|=18 cm and |OP’|=9 cm. What is the scale factor r? Show your work.
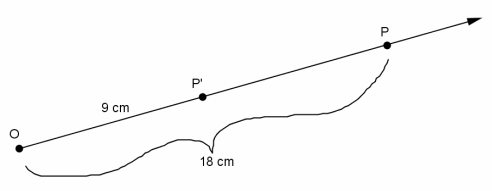
Answer:
Since |OP’ |=r|OP|, then
9 cm=r∙18 cm,
\(\frac{1}{2}\)=r.
Eureka Math Grade 8 Module 3 Lesson 1 Problem Set Answer Key
Have students practice using the definition of dilation and finding lengths according to a scale factor.
Question 1.
Let there be a dilation from center O. Then, Dilation(P)=P’ and Dilation(Q)=Q’. Examine the drawing below. What can you determine about the scale factor of the dilation?
Answer:
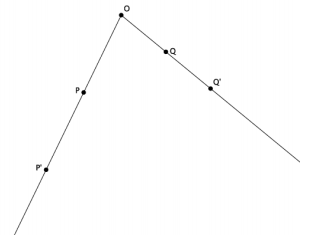
The scale factor must be greater than one, r>1, because the dilated points are farther from the center than the original points.
Question 2.
Let there be a dilation from center O. Then, Dilation(P)=P’, and Dilation(Q)=Q’. Examine the drawing below. What can you determine about the scale factor of the dilation?
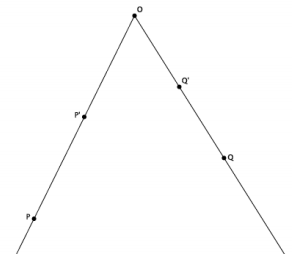
Answer:
The scale factor must be greater than zero but less than one, 0<r<1, because the dilated points are closer to the center than the original points.
Question 3.
Let there be a dilation from center O with a scale factor r=4. Then, Dilation(P)=P’ and Dilation(Q)=Q’. |OP|=3.2 cm, and |OQ|=2.7 cm, as shown. Use the drawing below to answer parts (a) and (b). The drawing is not to scale.
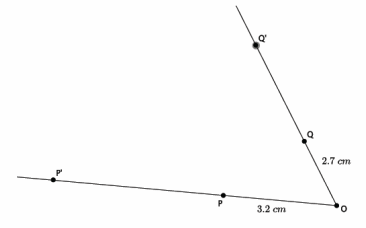
a. Use the definition of dilation to determine |OP’ |.
Answer:
|OP’ |=r|OP|; therefore, |OP’ |=4 (3.2 cm)=12.8 cm.
b. Use the definition of dilation to determine |OQ’ |.
Answer:
|OQ’ |=r|OQ|; therefore, |OQ’ |=4 (2.7 cm)=10.8 cm.
Question 4.
Let there be a dilation from center O with a scale factor r. Then, Dilation(A)=A’, Dilation(B)=B’, and Dilation(C)=C’. |OA|=3, |OB|=15, |OC|=6, and |OB’ |=5, as shown. Use the drawing below to answer parts (a)–(c).
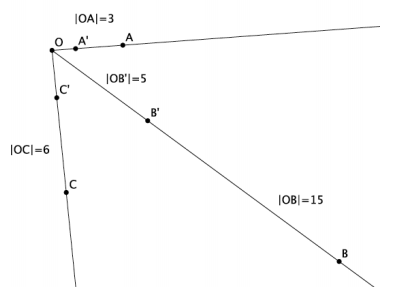
a. Using the definition of dilation with lengths OB and OB’, determine the scale factor of the dilation.
Answer:
|OB’ |=r|OB|, which means 5=r×15; therefore, r=\(\frac{1}{3}\).
b. Use the definition of dilation to determine |OA’|.
Answer:
|OA’ |=\(\frac{1}{3}\) |OA|; therefore, |OA’ |=\(\frac{1}{3}\)∙3=1, and |OA’|=1.
c. Use the definition of dilation to determine |OC’|.
Answer:
|OC’ |=\(\frac{1}{3}\) |OC|; therefore, |OC’|=\(\frac{1}{3}\)∙6=2, and |OC’|=2.