Eureka Math Grade 8 Module 3 Lesson 10 Answer Key

Eureka Math Grade 8 Module 3 Lesson 10 Answer Key

by

Engage NY Eureka Math 8th Grade Module 3 Lesson 10 Answer Key

Eureka Math Grade 8 Module 3 Lesson 10 Exercise Answer Key

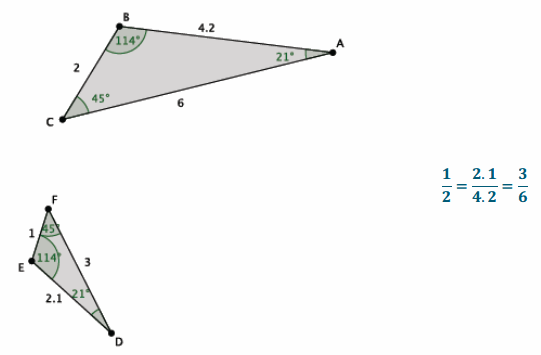
Exercises 1–2.
Use a protractor to draw a pair of triangles with two pairs of equal angles. Then, measure the lengths of the sides, and verify that the lengths of their corresponding sides are equal in ratio.
Answer:
Sample student work is shown below.
Eureka Math Grade 8 Module 3 Lesson 10 Exercise Answer Key 1

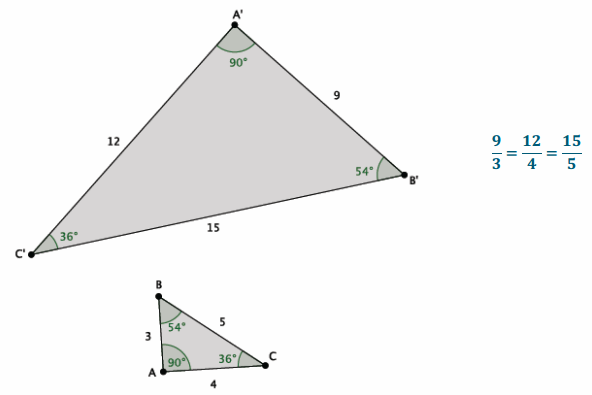
Exercise 2.
Draw a new pair of triangles with two pairs of equal angles. Then, measure the lengths of the sides, and verify that the lengths of their corresponding sides are equal in ratio.
Answer:
Sample student work is shown below.
Eureka Math Grade 8 Module 3 Lesson 10 Exercise Answer Key 2

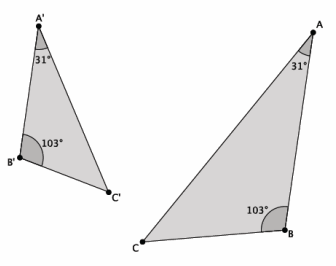
Exercises 3–5.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal, namely, |∠B|=|∠B’|=103°, and |∠A|=|∠A’|=31°.
Eureka Math Grade 8 Module 3 Lesson 10 Exercise Answer Key 3

Exercise 4.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
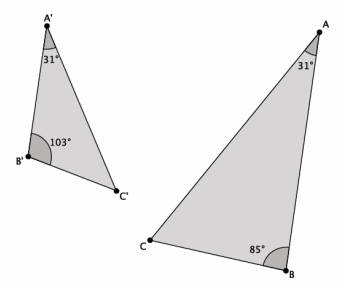
Eureka Math Grade 8 Module 3 Lesson 10 Exercise Answer Key 4
Answer:
No, △ABC is not similar to △A’ B’ C’. They are not similar because they do not have two pairs of corresponding angles that are equal, just one, namely, |∠A|=|∠A’|, but |∠B|≠|∠B’ |.

Exercise 5.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
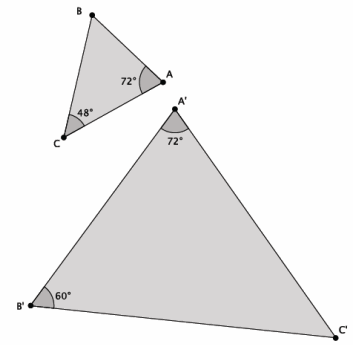
Eureka Math Grade 8 Module 3 Lesson 10 Exercise Answer Key 5
Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B|=60° or |∠C’|=48°. Then, you can see that |∠A|=|∠A’|=72°, |∠B|=|∠B’|=60°, and |∠C|=|∠C’|=48°.

Eureka Math Grade 8 Module 3 Lesson 10 Problem Set Answer Key

Eureka Math Grade 8 Module 3 Lesson 10 Problem Set Answer Key

Students practice presenting informal arguments to prove whether or not two triangles are similar.

Question 1.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
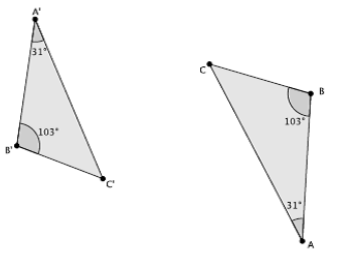
Eureka Math Grade 8 Module 3 Lesson 10 Problem Set Answer Key 8
Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal, namely, |∠B|=|∠B’|=103°, and |∠A|=|∠A’|=31°.

Question 2.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
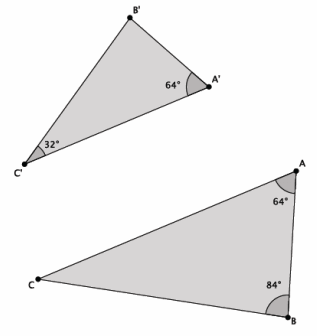
Eureka Math Grade 8 Module 3 Lesson 10 Problem Set Answer Key 9
Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B’|=84° or |∠C|=32°. Then, you can see that |∠A|=|∠A’|=64°, |∠B|=|∠B’|=84°, and |∠C|=|∠C’|=32°.

Question 3.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
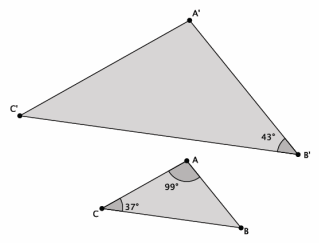
Eureka Math Grade 8 Module 3 Lesson 10 Problem Set Answer Key 10
Answer:
We do not know if △ABC is similar to △A’ B’ C’. We can use the triangle sum theorem to find out that |∠B|=44°, but we do not have any information about |∠A’| or |∠C’|. To be considered similar, the two triangles must have two pairs of corresponding angles that are equal. In this problem, we only know of one pair of corresponding angles, and that pair does not have equal measure.

Question 4.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
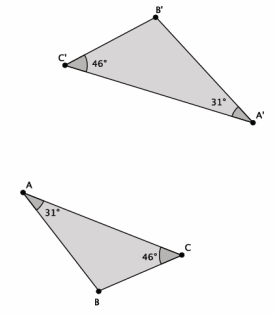
Eureka Math Grade 8 Module 3 Lesson 10 Problem Set Answer Key 11
Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal, namely, |∠C|=|∠C’|=46°, and |∠A|=|∠A’|=31°.

Question 5.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
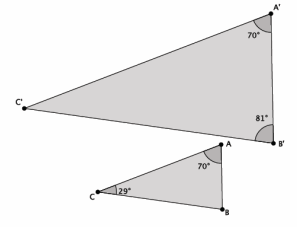
Eureka Math Grade 8 Module 3 Lesson 10 Problem Set Answer Key 12
Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B|=81° or |∠C’|=29°. Then, you can see that |∠A|=|∠A’|=70°, |∠B|=|∠B’|=81°,
and |∠C|=|∠C’|=29°.

Question 6.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
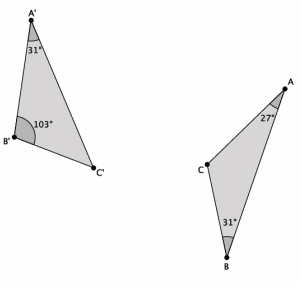
Eureka Math Grade 8 Module 3 Lesson 10 Problem Set Answer Key 13
Answer:
No, △ABC is not similar to △A’ B’ C’. By the given information, |∠B|≠|∠B’|, and |∠A|≠|∠A’|.

Question 7.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
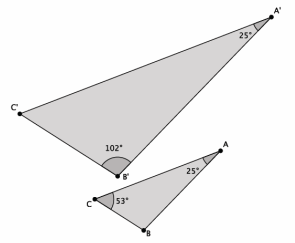
Eureka Math Grade 8 Module 3 Lesson 10 Problem Set Answer Key 14
Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B|=102° or |∠C’|=53°. Then, you can see that |∠A|=|∠A’|=25°, |∠B|=|∠B’|=102°, and |∠C|=|∠C’|=53°.

Eureka Math Grade 8 Module 3 Lesson 10 Exit Ticket Answer Key

Question 1.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
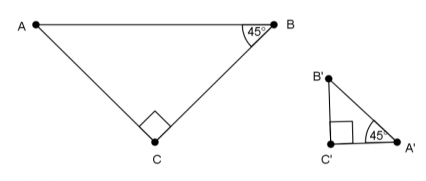
Engage NY Math 8th Grade Module 3 Lesson 10 Exit Ticket Answer Key 6
Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B’|=45˚or |∠A|=45˚. Then, you can see that |∠A|=|∠A’|=45˚, |∠B|=|∠B’|=45˚, and |∠C|=|∠C’|=90˚.

Question 2.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
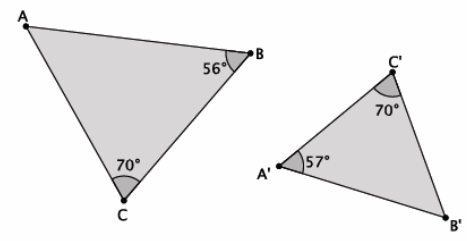
Engage NY Math 8th Grade Module 3 Lesson 10 Exit Ticket Answer Key 7
Answer:
No, △ABC is not similar to △A’ B’ C’. They are not similar because they do not have two pairs of corresponding angles that are equal, namely, |∠A|≠|∠A’ |, and |∠B|≠|∠B’|.

Leave a Comment