Engage NY Eureka Math 8th Grade Module 3 Lesson 4 Answer Key
Eureka Math Grade 8 Module 3 Lesson 4 Exercise Answer Key
Exercise
In the diagram below, points R and S have been dilated from center O by a scale factor of r=3.
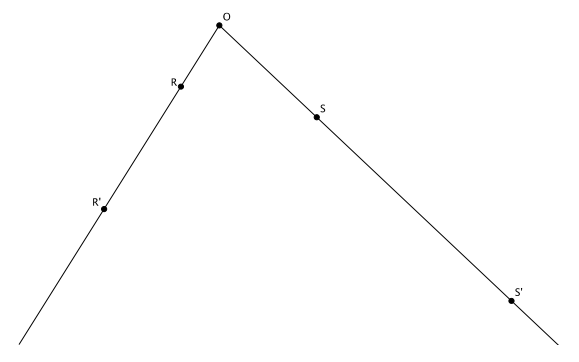
a. If |OR|=2.3 cm, what is |OR’|?
Answer:
|OR’|=3(2.3 cm)=6.9 cm
b. If |OS|=3.5 cm, what is |OS’|?
Answer:
|OS’|=3(3.5 cm)=10.5 cm
c. Connect the point R to the point S and the point R’ to the point S’. What do you know about the lines that contain segments RS and R’ S’?
Answer:
The lines containing the segments RS and R’S’ are parallel.
d. What is the relationship between the length of segment RS and the length of segment R’ S’?
Answer:
The length of segment R’ S’ is equal to the length of segment RS, times the scale factor of 3 (i.e., |R’ S’|=3|RS|).
e. Identify pairs of angles that are equal in measure. How do you know they are equal?
Answer:
|∠ORS|=|∠OR’ S’| and |∠OSR|=|∠OS’ R’| They are equal because they are corresponding angles of parallel lines cut by a transversal.
Eureka Math Grade 8 Module 3 Lesson 4 Problem Set Answer Key
Students verify that the fundamental theorem of similarity holds true when the scale factor r is 0<r<1.
Question 1.
Use a piece of notebook paper to verify the fundamental theorem of similarity for a scale factor r that is
0<r<1.
✓ Mark a point O on the first line of notebook paper.
✓ Mark the point P on a line several lines down from the center O. Draw a ray, \(\overrightarrow{O P}\). Mark the point P’ on the ray and on a line of the notebook paper closer to O than you placed point P. This ensures that you have a scale factor that is 0<r<1. Write your scale factor at the top of the notebook paper.
✓ Draw another ray, \(\overrightarrow{O Q}\), and mark the points Q and Q’ according to your scale factor.
✓ Connect points P and Q. Then, connect points P’ and Q’.
✓ Place a point, A, on the line containing segment PQ between points P and Q. Draw ray \(\overrightarrow{O A}\). Mark point A’ at the intersection of the line containing segment P’Q’ and ray \(\overrightarrow{O A}\).
Answer:
Sample student work is shown in the picture below:
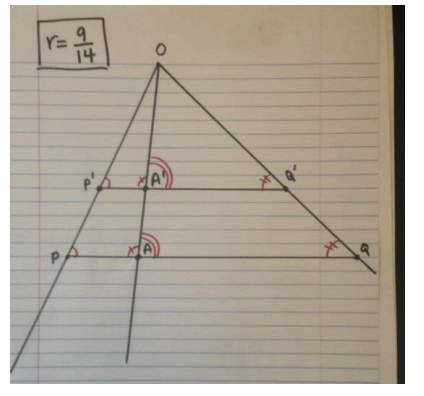
a. Are the lines containing segments PQ and P’Q’ parallel lines? How do you know?
Answer:
Yes, the lines containing segments PQ and P’Q’ are parallel. The notebook lines are parallel, and these lines fall on the notebook lines.
b. Which, if any, of the following pairs of angles are equal in measure? Explain.
i. ∠OPQ and ∠OP’Q’
ii. ∠OAQ and ∠OA’Q’
iii. ∠OAP and ∠OA’P’
iv. ∠OQP and ∠OQ’P’
Answer:
All four pairs of angles are equal in measure because each pair of angles are corresponding angles of parallel lines cut by a transversal. In each case, the parallel lines are line PQ and line P’ Q’, and the transversal is the respective ray.
c. Which, if any, of the following statements are true? Show your work to verify or dispute each statement.
i. |OP’|=r|OP|
ii. |OQ’|=r|OQ|
iii. |P’A’|=r|PA|
iv. |A’Q’|=r|AQ|
Answer:
All four of the statements are true. Verify that students have shown that the length of the dilated segment was equal to the scale factor multiplied by the original segment length.
d. Do you believe that the fundamental theorem of similarity (FTS) is true even when the scale factor is 0<r<1? Explain.
Answer:
Yes, because I just experimentally verified the properties of FTS for when the scale factor is 0<r<1.
Question 2.
Caleb sketched the following diagram on graph paper. He dilated points B and C from center O.
Answer:
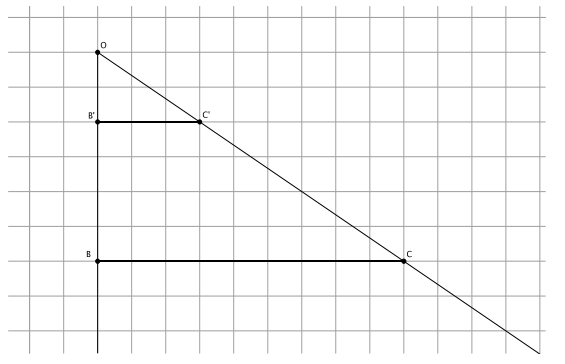
a. What is the scale factor r? Show your work.
Answer:
|OB’|=r|OB|
2=r∙6
\(\frac{2}{6}\)=r
\(\frac{1}{3}\)=r
b. Verify the scale factor with a different set of segments.
Answer:
|B’ C’|=r|BC|
3=r∙9
\(\frac{3}{9}\)=r
\(\frac{1}{3}\)=r
c. Which segments are parallel? How do you know?
Answer:
Segment BC and B’C’ are parallel. They lie on the lines of the graph paper, which are parallel.
d. Which angles are equal in measure? How do you know?
Answer:
|∠OB’ C’|=|∠OBC|, and |∠OC’ B’|=|∠OCB| because they are corresponding angles of parallel lines cut by a transversal.
Question 3.
Points B and C were dilated from center O.
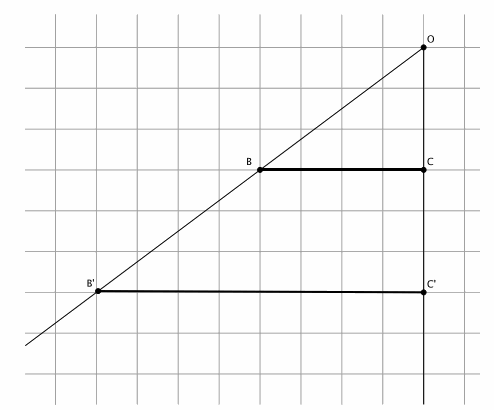
a. What is the scale factor r? Show your work.
Answer:
|OC’|=r|OC|
6=r∙3
\(\frac{6}{3}\)=r
2=r
b. If |OB|=5, what is |OB’|?
Answer:
|OB’|=r|OB|
|OB’|=2∙5
|OB’|=10
c. How does the perimeter of triangle OBC compare to the perimeter of triangle OB’C’?
Answer:
The perimeter of triangle OBC is 12 units, and the perimeter of triangle OB’C’ is 24 units.
d. Did the perimeter of triangle OB’C’=r×(perimeter of triangle OBC)? Explain.
Answer:
Yes, the perimeter of triangle OB’C’ was twice the perimeter of triangle OBC, which makes sense because the dilation increased the length of each segment by a scale factor of 2. That means that each side of triangle OB’C’ was twice as long as each side of triangle OBC.
Eureka Math Grade 8 Module 3 Lesson 4 Exit Ticket Answer Key
Steven sketched the following diagram on graph paper. He dilated points B and C from point O. Answer the following questions based on his drawing.
Question 1.
What is the scale factor r? Show your work.
Answer:
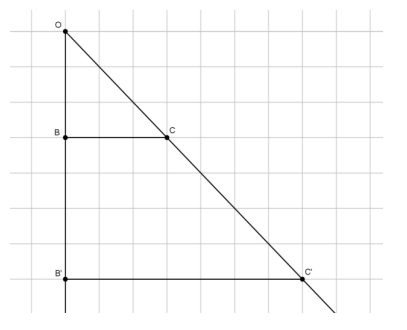
|OB’|=r|OB|
7=r∙3
\(\frac{7}{3}\)=r
Question 2.
Verify the scale factor with a different set of segments.
Answer:
|B’ C’|=r|BC|
7=r∙3
\(\frac{7}{3}\)=r
Question 3.
Which segments are parallel? How do you know?
Answer:
Segments BC and B’C’ are parallel since they lie on the grid lines of the paper, which are parallel.
Question 4.
Are ∠OBC and ∠OB’C’ right angles? How do you know?
Answer:
The grid lines on graph paper are perpendicular, and since perpendicular lines form right angles, ∠OBC and ∠OB’C’ are right angles.