Engage NY Eureka Math 8th Grade Module 3 Lesson 5 Answer Key
Eureka Math Grade 8 Module 3 Lesson 5 Exercise Answer Key
Exercise 1.
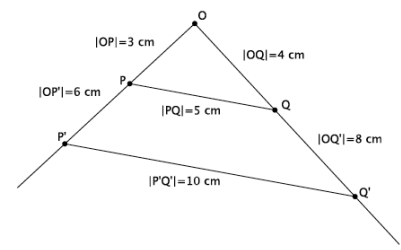
In the diagram below, points P and Q have been dilated from center O by scale factor r. \(\overline{P Q}\) || \(\overline{\boldsymbol{P}^{\prime} \boldsymbol{Q}^{\prime}}\) |PQ|=5 cm, and |P’Q’|=10 cm.
b. Determine the scale factor r.
Answer:
According to FTS, |P’Q’|=r|PQ|. Therefore, 10=r∙5, so r=2.
b. Locate the center O of dilation. Measure the segments to verify that |OP’|=r|OP| and |OQ’|=r|OQ|. Show your work below.
Answer:
Center O and measurements are shown above.
|OP’|=r|OP|
6=2∙3
6=6
|OQ’|=r|OQ|
8=2∙4
8=8
Exercise 2.
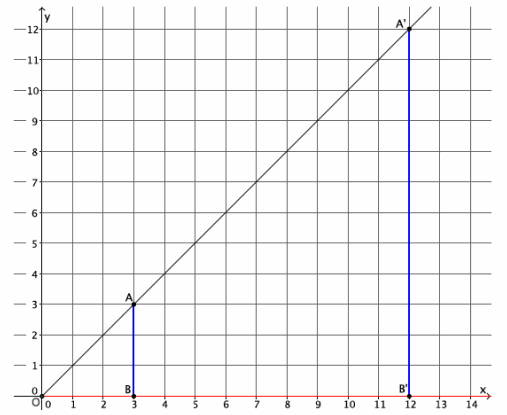
In the diagram below, you are given center O and ray \(\overrightarrow{0 A}\). Point A is dilated by a scale factor r=4. Use what you know about FTS to find the location of point A’.
Answer:
Point A’ must be located at (12,12).
Exercise 3.
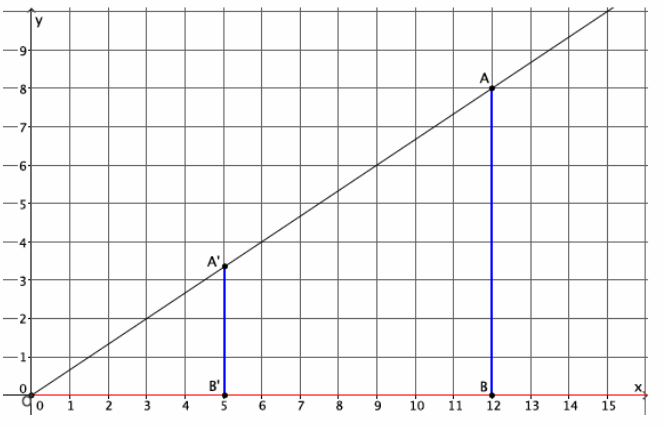
In the diagram below, you are given center O and ray \(\overrightarrow{0 A}\). Point A is dilated by a scale factor r=\(\frac{5}{12}\). Use what you know about FTS to find the location of point A’.
Answer:
The x-coordinate of A’ is 5. The y-coordinate is equal to the length of segment A’B’. Since |A’B’|=r|AB|, then |A’B’|=\(\frac{5}{12}\)∙8=\(\frac{40}{12}\)≈3.3. The location of A’ is (5,3.3).
Eureka Math Grade 8 Module 3 Lesson 5 Exit Ticket Answer Key
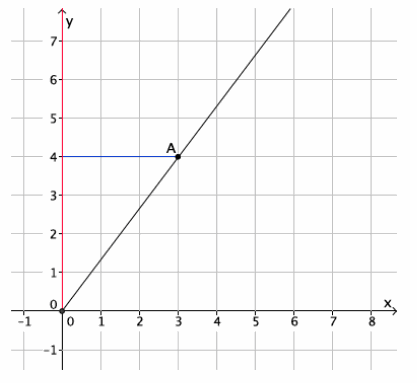
In the diagram below, you are given center O and ray \(\overrightarrow{O A}\). Point A is dilated by a scale factor r= \(\frac{6}{4}\). Use what you know about FTS to find the location of point A’.
Answer:
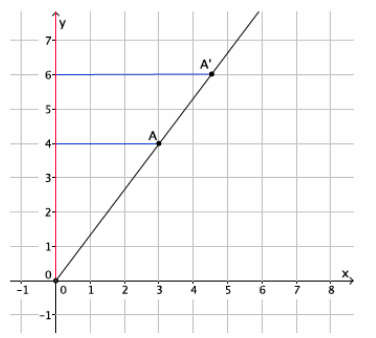
The y-coordinate of A’ is 6. The x-coordinate is equal to the length of segment A’B’. Since |A’B’|=r|AB|, then
|A’B’|=\(\frac{6}{4}\)∙3=\(\frac{18}{4}\)=4.5. The location of A’ is (4.5,6).
Eureka Math Grade 8 Module 3 Lesson 5 Problem Set Answer Key
Students practice using the first consequences of FTS in terms of dilated points and their locations on the coordinate plane.
Question 1.
Dilate point A, located at (3,4) from center O, by a scale factor r=\(\frac{5}{3}\).
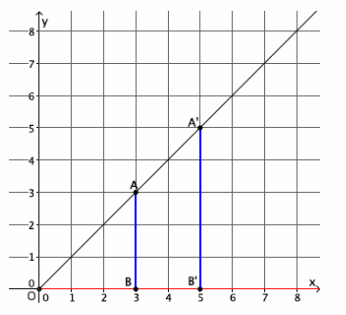
What is the precise location of point A’?
Answer:
The y-coordinate of point A’ is the length of segment A’B’. Since |A’B’|=r|AB|, then |A’B’|=\(\frac{5}{3}\)∙4=\(\frac{20}{3}\). The location of point A’ is
(5,\(\frac{20}{3}\)), or approximately (5,6.7).
Question 2.
Dilate point A, located at (9,7) from center O, by a scale factor r=\(\frac{4}{9}\). Then, dilate point B, located at (9,5) from center O, by a scale factor of r=\(\frac{4}{9}\). What are the coordinates of points A’ and B’? Explain.
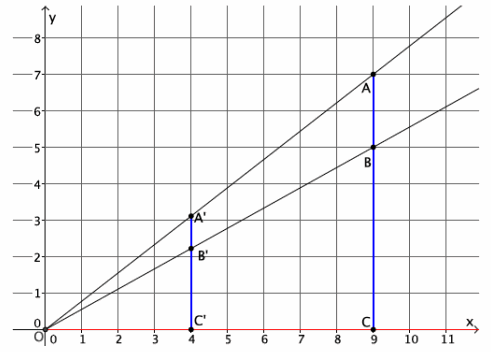
Answer:
The y-coordinate of point A’ is the length of A’C’. Since |A’C’|=r|AC|, then |A’C’|=\(\frac{4}{9}\)∙7=\(\frac{28}{9}\). The location of point A’ is (4, \(\frac{28}{9}\)), or approximately (4,3.1). The y-coordinate of point B’ is the length of B’C’. Since |B’C’|=r|BC|, then |B’C’|=\(\frac{4}{9}\)∙5=\(\frac{20}{9}\). The location of point B’ is (4, \(\frac{20}{9}\)), or approximately (4,2.2).
Question 3.
Explain how you used the fundamental theorem of similarity in Problems 1 and 2.
Answer:
Using what I knew about scale factor, I was able to determine the placement of points A’ and B’, but I did not know the actual coordinates. So, one of the ways that FTS was used was actually in terms of the converse of FTS. I had to make sure I had parallel lines. Since the lines of the coordinate plane guarantee parallel lines, I knew that |A’C’|=r|AC|. Then, since I knew the length of segment AC and the scale factor, I could find the precise location of A’. The precise location of B’ was found in a similar way but using |B’C’|=r|BC|.