Engage NY Eureka Math 8th Grade Module 4 Lesson 19 Answer Key
Eureka Math Grade 8 Module 4 Lesson 19 Exercise Answer Key
Exercises 1 – 11
THEOREM: The graph of a linear equation y = mx + b is a non – vertical line with slope m and passing through (0, b), where b is a constant.
Exercise 1.
Prove the theorem by completing parts (a)–(c). Given two distinct points, P and Q, on the graph of y = mx + b, and let l be the line passing through P and Q. You must show the following:
(1) Any point on the graph of y = mx + b is on line l, and
(2) Any point on the line l is on the graph of y = mx + b.
a. Proof of (1): Let R be any point on the graph of y = mx + b. Show that R is on l. Begin by assuming it is not. Assume the graph looks like the diagram below where R is on l’.
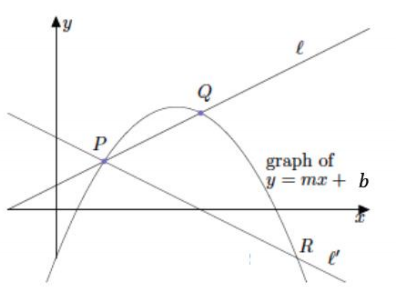
What is the slope of line l?
Answer:
Since the points P and Q are on the graph of y = mx + b, then we know that the slope of the line passing through those points must have slope m. Therefore, line l has slope m.
What is the slope of line l’?
Answer:
We know that point R is on the graph of y = mx + b. Then the coordinates of point R are (r1, mr1 + b) because R is a solution to y = mx + b, and r2 = mr1 + b. Similarly, the coordinates of P are (p1, mp1 + b).
Answer:
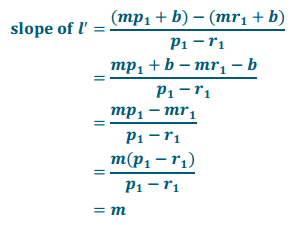
What can you conclude about lines l and l’? Explain.
Answer:
Lines l and l’are the same line. Both lines go through point P and have slope m. There can be only one line with a given slope going through a given point; therefore, line l is the same as l’.
b. Proof of (2): Let S be any point on line l, as shown.
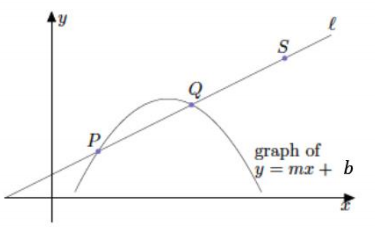
Show that S is a solution to y = mx + b. Hint: Use the point (0, b).
Answer:
Point S is on line l. Let S = (s1, s2).
slope of l = \(\frac{s_{2} – b}{s_{1} – 0}\)
We know the slope of l is m.
m = \(\frac{s_{2} – b}{s_{1} – 0}\)
m(s1 – 0) = s2 – b
ms1 = s2 – b
ms1 + b = s2 – b + b
ms1 + b = s2
s2 = ms1 + b,
which shows S is a solution to y = mx + b.
c. Now that you have shown that any point on the graph of y = mx + b is on line l in part (a), and any point on line l is on the graph of y = mx + b in part (b), what can you conclude about the graphs of linear equations?
Answer:
The graph of a linear equation is a line.
Exercise 2.
Use x = 4 and x = – 4 to find two solutions to the equation x + 2y = 6. Plot the solutions as points on the coordinate plane, and connect the points to make a line.
Answer:
The solutions are (4, 1) and ( – 4, 5).
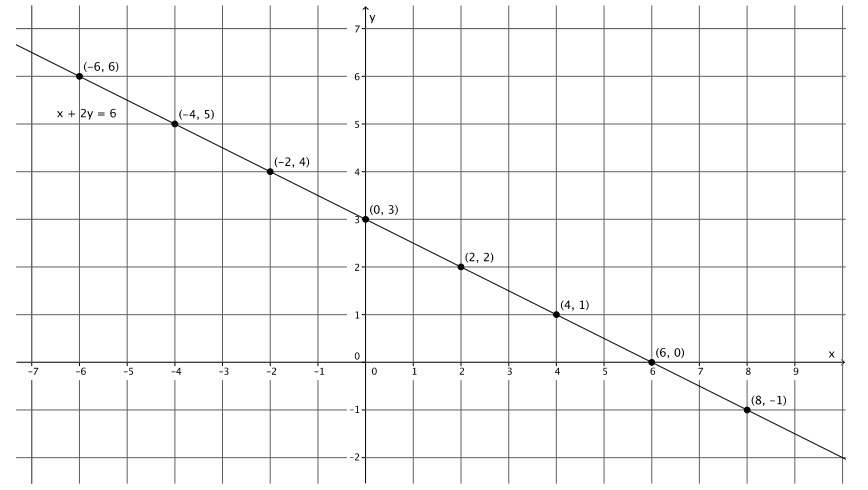
a. Identify two other points on the line with integer coordinates. Verify that they are solutions to the equation x + 2y = 6.
Answer:
The choice of points and verifications will vary. Several possibilities are noted in the graph above.
b. When x = 1, what is the value of y? Does this solution appear to be a point on the line?
Answer:
1 + 2y = 6
2y = 5
y = \(\frac{5}{2}\)
Yes, (1, \(\frac{5}{2}\)) does appear to be a point on the line.
c. When x = – 3, what is the value of y? Does this solution appear to be a point on the line?
Answer:
– 3 + 2y = 6
2y = 9
y = \(\frac{9}{2}\)
Yes, ( – 3, \(\frac{9}{2}\)) does appear to be a point on the line.
d. Is the point (3, 2) on the line?
Answer:
No, (3, 2) is not a point on the line.
e. Is the point (3, 2) a solution to the linear equation x + 2y = 6?
Answer:
No, (3, 2) is not a solution to x + 2y = 6.
3 + 2(2) = 6
3 + 4 = 6
7≠6
Exercise 3.
Use x = 4 and x = 1 to find two solutions to the equation 3x – y = 9. Plot the solutions as points on the coordinate plane, and connect the points to make a line.
Answer:
The solutions are (4, 3) and (1, – 6).
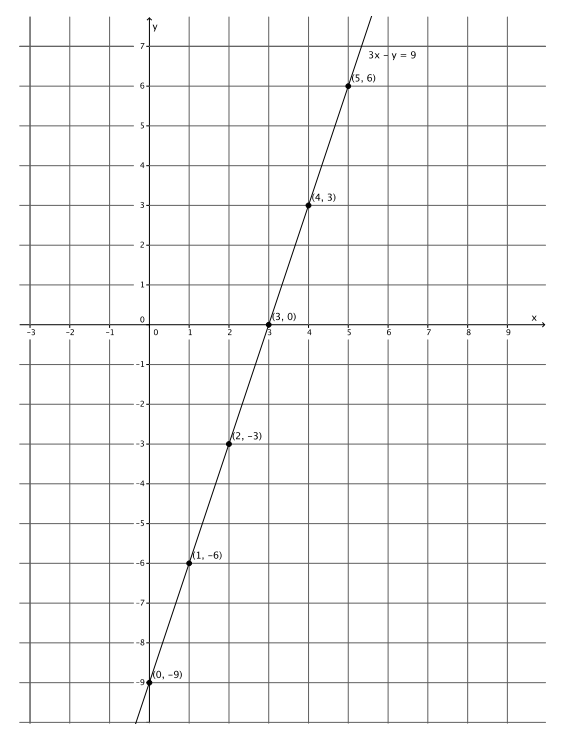
a. Identify two other points on the line with integer coordinates. Verify that they are solutions to the equation 3x – y = 9.
Answer:
The choice of points and verifications will vary. Several possibilities are noted in the graph above.
b. When x = 4.5, what is the value of y? Does this solution appear to be a point on the line?
Answer:
3(4.5) – y = 9
13.5 – y = 9
– y = – 4.5
y = 4.5
Yes, (4.5, 4.5) does appear to be a point on the line.
c. When x = \(\frac{1}{2}\), what is the value of y? Does this solution appear to be a point on the line?
Answer:
3(\(\frac{1}{2}\)) – y = 9
\(\frac{3}{2}\) – y = 9
– y = \(\frac{15}{2}\)
y = – \(\frac{15}{2}\)
Yes, (\(\frac{1}{2}\), – \(\frac{15}{2}\)) does appear to be a point on the line.
d. Is the point (2, 4) on the line?
Answer:
No, (2, 4) is not a point on the line.
e. Is the point (2, 4) a solution to the linear equation 3x – y = 9?
Answer:
No, (2, 4) is not a solution to 3x – y = 9.
3(2) – 4 = 9
6 – 4 = 9
2≠9
Exercise 4.
Use x = 3 and x = – 3 to find two solutions to the equation 2x + 3y = 12. Plot the solutions as points on the coordinate plane, and connect the points to make a line.
Answer:
The solutions are ( – 3, 6) and (3, 2).
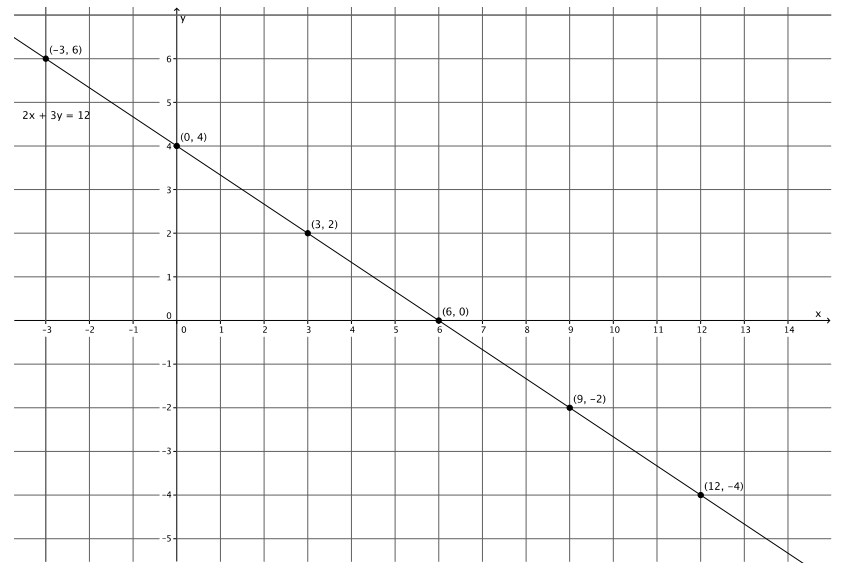
a. Identify two other points on the line with integer coordinates. Verify that they are solutions to the equation 2x + 3y = 12.
Answer:
The choice of points and verifications will vary. Several possibilities are noted in the graph above.
b. When x = 2, what is the value of y? Does this solution appear to be a point on the line?
Answer:
2(2) + 3y = 12
4 + 3y = 12
3y = 8
y = \(\frac{8}{3}\)
Yes, (2, \(\frac{8}{3}\)) does appear to be a point on the line.
c. When x = – 2, what is the value of y? Does this solution appear to be a point on the line?
Answer:
2( – 2) + 3y = 12
– 4 + 3y = 12
3y = 16
y = \(\frac{16}{3}\)
Yes, ( – 2, \(\frac{16}{3}\)) does appear to be a point on the line.
d. Is the point (8, – 3) on the line?
Answer:
No, (8, – 3) is not a point on the line.
e. Is the point (8, – 3) a solution to the linear equation 2x + 3y = 12?
Answer:
No, (8, – 3) is not a solution to 2x + 3y = 12.
2(8) + 3( – 3) = 12
16 – 9 = 12
7≠12
Exercise 5.
Use x = 4 and x = – 4 to find two solutions to the equation x – 2y = 8. Plot the solutions as points on the coordinate plane, and connect the points to make a line.
Answer:
The solutions are (4, – 2) and ( – 4, – 6).
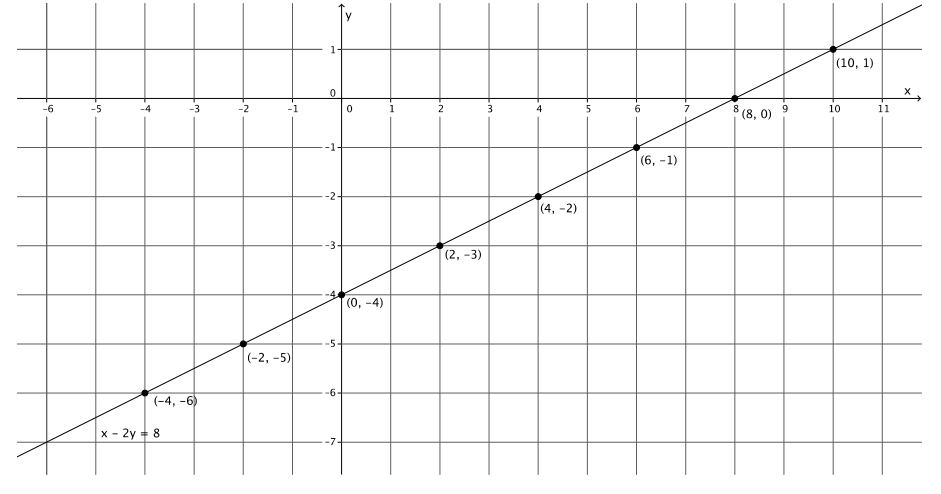
a. Identify two other points on the line with integer coordinates. Verify that they are solutions to the equation x – 2y = 8.
Answer:
The choice of points and verifications will vary. Several possibilities are noted in the graph above.
b. When x = 7, what is the value of y? Does this solution appear to be a point on the line?
Answer:
7 – 2y = 8
– 2y = 1
y = – \(\frac{1}{2}\)
Yes, (7, – \(\frac{1}{2}\)) does appear to be a point on the line.
c. When x = – 3, what is the value of y? Does this solution appear to be a point on the line?
Answer:
– 3 – 2y = 8
– 2y = 11
y = – \(\frac{11}{2}\)
Yes, ( – 3, – \(\frac{11}{2}\)) does appear to be a point on the line.
d. Is the point ( – 2, – 3) on the line?
Answer:
No, ( – 2, – 3) is not a point on the line.
e. Is the point ( – 2, – 3) a solution to the linear equation x – 2y = 8?
Answer:
No, ( – 2, – 3) is not a solution to x – 2y = 8.
– 2 – 2( – 3) = 8
– 2 + 6 = 8
4≠8
Exercise 6.
Based on your work in Exercises 2–5, what conclusions can you draw about the points on a line and solutions to a linear equation?
Answer:
It appears that all points on the line represent a solution to the equation. In other words, any point identified on the line is a solution to the linear equation.
Exercise 7.
Based on your work in Exercises 2–5, will a point that is not a solution to a linear equation be a point on the graph of a linear equation? Explain.
Answer:
No. Each time we were given a point off the line in part (d), we verified that it was not a solution to the equation in part (e). For that reason, I would expect that all points not on the line would not be a solution to the equation.
Exercise 8.
Based on your work in Exercises 2–5, what conclusions can you draw about the graph of a linear equation?
Answer:
The graph of a linear equation is a line.
Exercise 9.
Graph the equation – 3x + 8y = 24 using intercepts.
Answer:
– 3x + 8y = 24
– 3(0) + 8y = 24
8y = 24
y = 3
The y – intercept point is (0, 3).
– 3x + 8y = 24
– 3x + 8(0) = 24
– 3x = 24
x = – 8
The x – intercept point is ( – 8, 0).
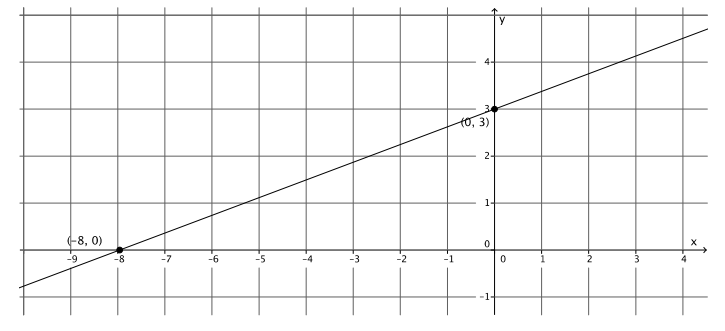
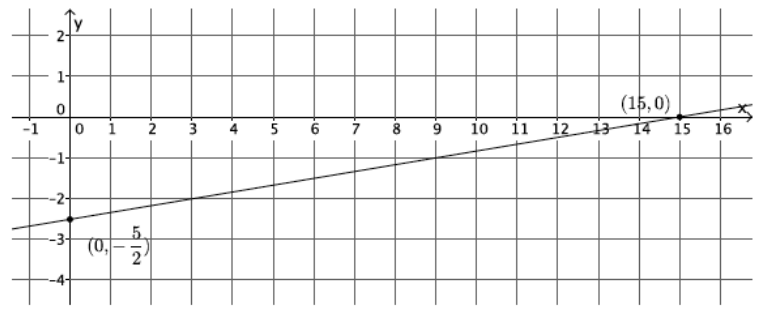
Exercise 10.
Graph the equation x – 6y = 15 using intercepts.
Answer:
x – 6y = 15
0 – 6y = 15
– 6y = 15
y = – \(\frac{15}{6}\)
y = – \(\frac{5}{2}\)
The y – intercept point is (0, – \(\frac{5}{2}\)).
x – 6y = 15
x – 6(0) = 15
x = 15
The x – intercept point is (15, 0).
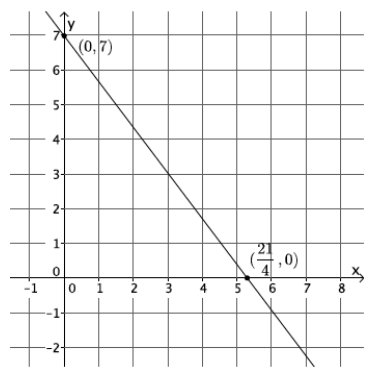
Exercise 11.
Graph the equation 4x + 3y = 21 using intercepts.
Answer:
4x + 3y = 21
4(0) + 3y = 21
3y = 21
y = 7
The y – intercept point is (0, 7).
4x + 3y = 21
4x + 3(0) = 21
4x = 21
x = 21/4
The x – intercept point is (21/4, 0).
Eureka Math Grade 8 Module 4 Lesson 19 Problem Set Answer Key
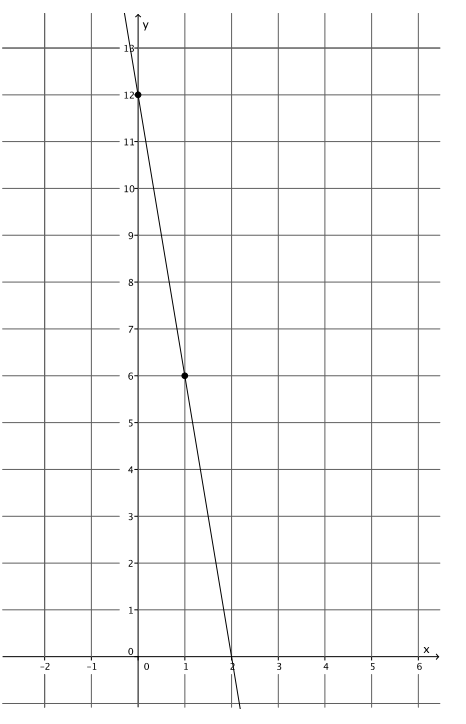
Question 1.
Graph the equation: y = – 6x + 12.
Answer:
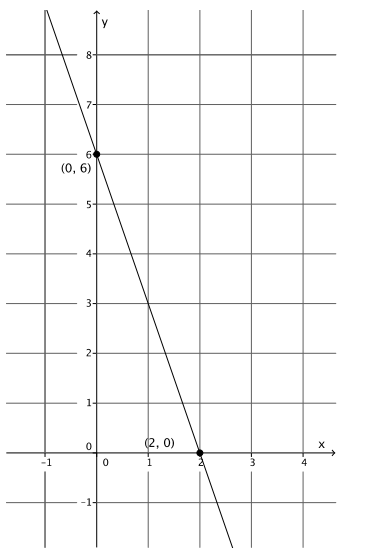
Question 2.
Graph the equation: 9x + 3y = 18.
Answer:
9(0) + 3y = 18
3y = 18
y = 6
The y – intercept point is (0, 6).
9x + 3(0) = 18
9x = 18
x = 2
The x – intercept point is (2, 0).
Question 3.
Graph the equation: y = 4x + 2.
Answer:
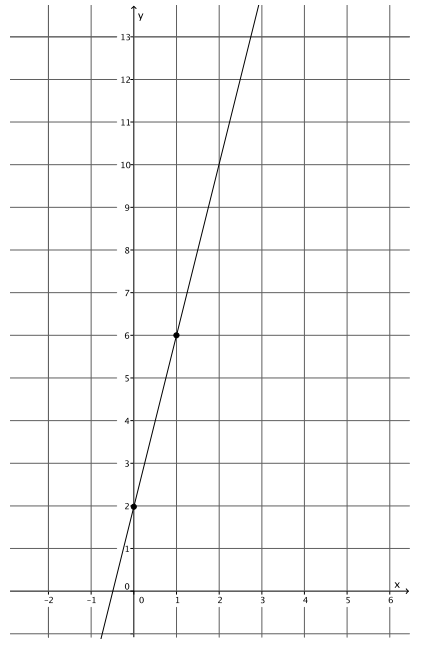
Question 4.
Graph the equation: y = – \(\frac{5}{7}\) x + 4.
Answer:
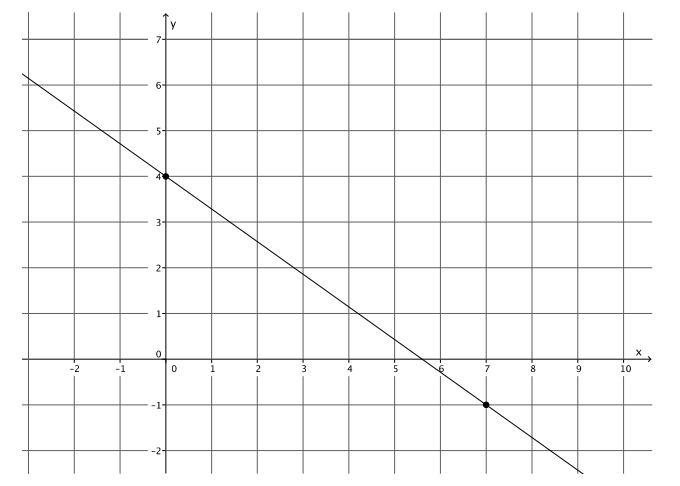
Question 5.
Graph the equation: \(\frac{3}{4}\) x + y = 8.
Answer:
\(\frac{3}{4}\) (0) + y = 8
y = 8
The y – intercept point is (0, 8).
\(\frac{3}{4}\) x + 0 = 8
\(\frac{3}{4}\) x = 8
x = \(\frac{32}{3}\)
The x – intercept point is (\(\frac{32}{3}\), 0).
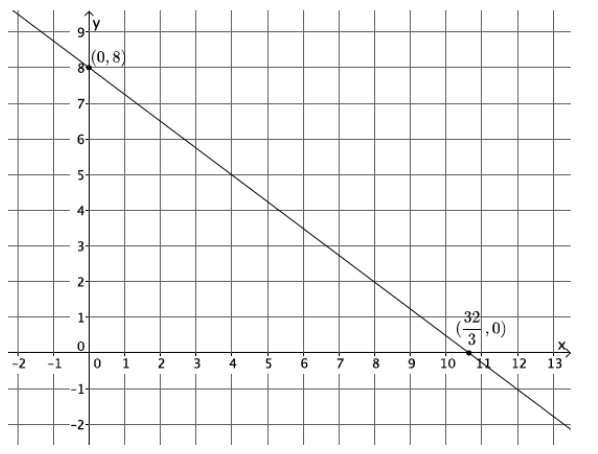
Question 6.
Graph the equation: 2x – 4y = 12.
Answer:
2(0) – 4y = 12
– 4y = 12
y = – 3
The y – intercept point is (0, – 3).
2x – 4(0) = 12
2x = 12
x = 6
The x – intercept point is (6, 0).
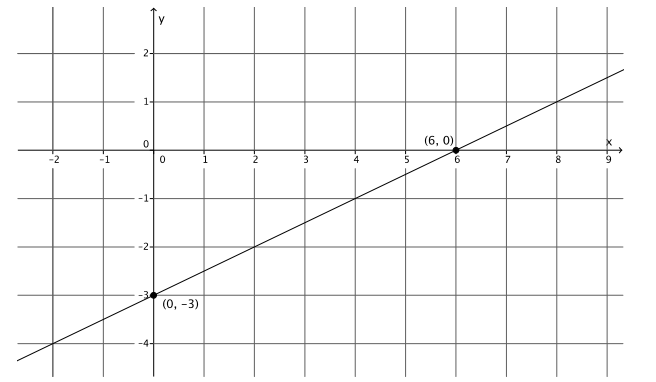
Question 7.
Graph the equation: y = 3. What is the slope of the graph of this line?
Answer:
The slope of this line is zero.
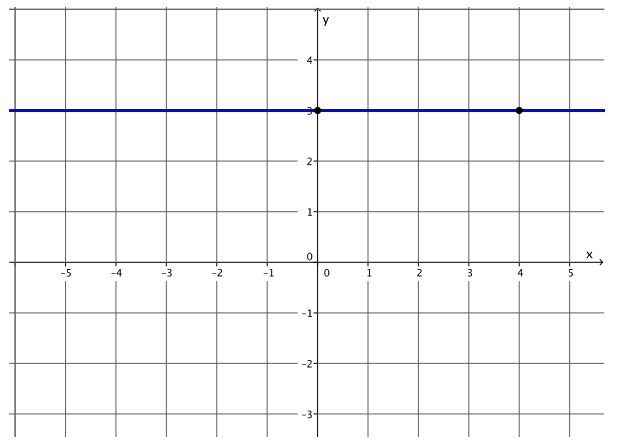
Question 8.
Graph the equation: x = – 4. What is the slope of the graph of this line?
Answer:
The slope of this line is undefined.
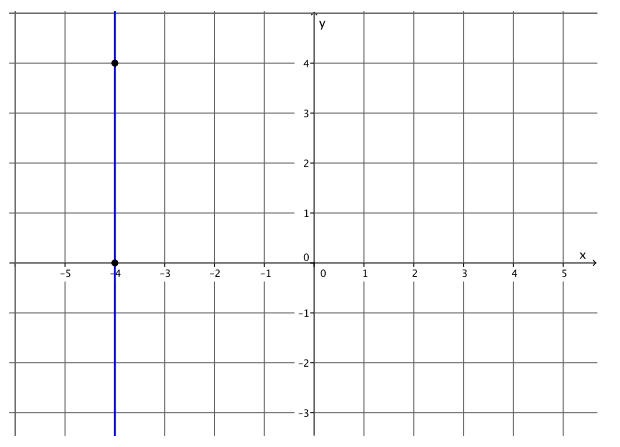
Question 9.
Is the graph of 4x + 5y = \(\frac{3}{7}\) a line? Explain.
Answer:
Yes, the graph of 4x + 5y = \(\frac{3}{7}\) is a line because it is a linear equation comprising linear expressions on both sides of the equal sign.
Question 10.
Is the graph of 6x2 – 2y = 7 a line? Explain.
Answer:
Maybe. The equation 6x2 – 2y = 7 is not a linear equation because the expression on the left side of the equal sign is not a linear expression. If this were a linear equation, then I would be sure that it graphs as a line, but because it is not, I am not sure what the graph of this equation would look like.
Eureka Math Grade 8 Module 4 Lesson 19 Exit Ticket Answer Key
Question 1.
Graph the equation y = \(\frac{5}{4}\) x – 10 using the y – intercept point and slope.
Answer:
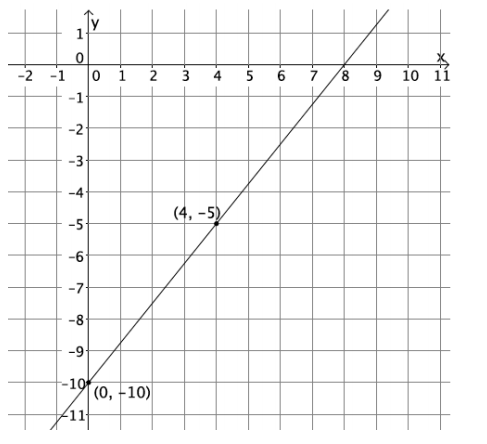
Question 2.
Graph the equation 5x – 4y = 40 using intercepts.
Answer:
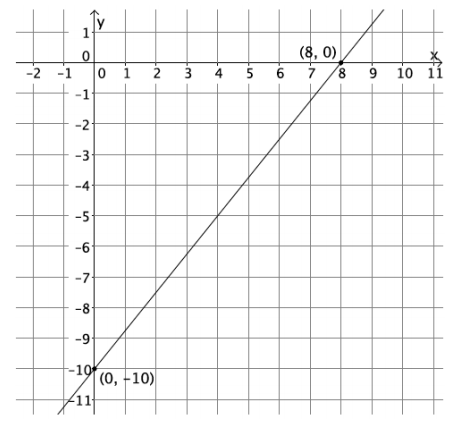
Question 3.
What can you conclude about the equations y = \(\frac{5}{4}\) x – 10 and 5x – 4y = 40?
Answer:
Since the points (0, – 10), (4, – 5), and (8, 0) are common to both graphs, then the lines must be the same. There is only one line that can pass through two points. If you transform the equation y = \(\frac{5}{4}\) x – 10 so that it is in standard form, it is the equation 5x – 4y = 40.