Engage NY Eureka Math 8th Grade Module 4 Lesson 31 Answer Key
Eureka Math Grade 8 Module 4 Lesson 31 Exercise Answer Key
Exercises
Exercise 1.
Identify two Pythagorean triples using the known triple 3, 4, 5 (other than 6, 8, 10).
Answer:
Answers will vary. Accept any triple that is a whole number multiple of 3, 4, 5.
Exercise 2.
Identify two Pythagorean triples using the known triple 5, 12, 13.
Answer:
Answers will vary. Accept any triple that is a whole number multiple of 5, 12, 13.
Exercise 3.
Identify two triples using either 3, 4, 5 or 5, 12, 13.
Answer:
Answers will vary.
Use the system 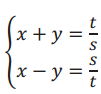 to find Pythagorean triples for the given values of s and t. Recall that the solution in the form of (\(\frac{c}{b}\), \(\frac{a}{b}\)) is the triple a, b, c.
to find Pythagorean triples for the given values of s and t. Recall that the solution in the form of (\(\frac{c}{b}\), \(\frac{a}{b}\)) is the triple a, b, c.
Exercise 4.
s = 4, t = 5
Answer:
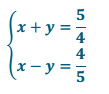
x + y + x – y = \(\frac{5}{4}\) + \(\frac{4}{5}\)
2x = \(\frac{5}{4}\) + \(\frac{4}{5}\)
2x = \(\frac{41}{20}\)
x = \(\frac{41}{40}\)
\(\frac{41}{40}\) + y = \(\frac{5}{4}\)
y = \(\frac{5}{4}\) – \(\frac{41}{40}\)
y = \(\frac{9}{40}\)
Then the solution is (\(\frac{41}{40}\), \(\frac{9}{40}\)), and the triple is 9, 40, 41.
Exercise 5.
s = 7, t = 10
Answer:
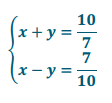
x + y + x – y = \(\frac{10}{7}\) + \(\frac{7}{10}\)
2x = \(\frac{149}{70}\)
x = \(\frac{149}{140}\)
\(\frac{149}{140}\) + y = \(\frac{10}{7}\)
y = \(\frac{10}{7}\) – \(\frac{149}{140}\)
y = \(\frac{51}{140}\)
Then the solution is (\(\frac{149}{140}\), \(\frac{51}{140}\)), and the triple is 51, 140, 149.
Exercise 6.
s = 1, t = 4
Answer:
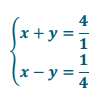
x + y + x – y = 4 + \(\frac{1}{4}\)
2x = \(\frac{17}{4}\)
x = \(\frac{17}{8}\)
\(\frac{17}{8}\) + y = \(\frac{4}{1}\)
y = 4 – \(\frac{17}{8}\)
y = \(\frac{15}{8}\)
Then the solution is (\(\frac{17}{8}\), \(\frac{15}{8}\)), and the triple is 15, 8, 17.
Exercise 7.
Use a calculator to verify that you found a Pythagorean triple in each of the Exercises 4–6. Show your work below.
Answer:
For the triple 9, 40, 41:
92 + 402 = 412
81 + 1600 = 1681
1681 = 1681
For the triple 51, 140, 149:
512 + 1402 = 1492
2601 + 19600 = 22201
22201 = 22201
For the triple 15, 8, 17:
152 + 82 = 172
225 + 64 = 289
289 = 289
Eureka Math Grade 8 Module 4 Lesson 31 Problem Set Answer Key
Question 1.
Explain in terms of similar triangles why it is that when you multiply the known Pythagorean triple 3, 4, 5 by 12, it generates a Pythagorean triple.
Answer:
The triangle with lengths 3, 4, 5 is similar to the triangle with lengths 36, 48, 60. They are both right triangles whose corresponding side lengths are equal to the same constant.
\(\frac{36}{3}\) = \(\frac{48}{4}\) = \(\frac{60}{5}\) = 12
Therefore, the triangles are similar, and we can say that there is a dilation from some center with scale factor r = 12 that makes the triangles congruent.
Question 2.
Identify three Pythagorean triples using the known triple 8, 15, 17.
Answer:
Answers will vary. Accept any triple that is a whole number multiple of 8, 15, 17.
Question 3.
Identify three triples (numbers that satisfy a2 + b2 = c2, but a, b, c are not whole numbers) using the triple 8, 15, 17.
Answer:
Answers will vary. Accept any triple that is not a set of whole numbers.
Use the system 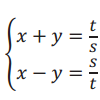 to find Pythagorean triples for the given values of s and t. Recall that the solution, in the form of (c/b, a/b), is the triple, a, b, c.
to find Pythagorean triples for the given values of s and t. Recall that the solution, in the form of (c/b, a/b), is the triple, a, b, c.
Question 4.
s = 2, t = 9
Answer:
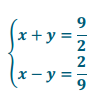
x + y + x – y = \(\frac{9}{2}\) + \(\frac{2}{9}\)
2x = \(\frac{85}{18}\)
x = \(\frac{85}{36}\)
\(\frac{85}{36}\) + y = \(\frac{9}{2}\)
y = \(\frac{9}{2}\) – \(\frac{85}{36}\)
y = \(\frac{77}{36}\)
Then the solution is (\(\frac{85}{36}\), \(\frac{77}{36}\)), and the triple is 77, 36, 85.
Question 5.
s = 6, t = 7
Answer:
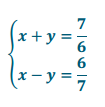
x + y + x – y = \(\frac{7}{6}\) + 6/7
2x = \(\frac{85}{42}\)
x = \(\frac{85}{84}\)
\(\frac{85}{84}\) + y = \(\frac{7}{6}\)
y = \(\frac{7}{6}\) – \(\frac{85}{84}\)
y = \(\frac{13}{84}\)
Then the solution is (\(\frac{85}{84}\), \(\frac{13}{84}\)), and the triple is 13, 84, 85.
Question 6.
s = 3, t = 4
Answer:
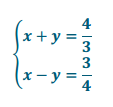
x + y + x – y = \(\frac{4}{3}\) + \(\frac{3}{4}\)
2x = \(\frac{25}{12}\)
x = \(\frac{25}{24}\)
\(\frac{25}{24}\) + y = \(\frac{4}{3}\)
y = \(\frac{4}{3}\) – \(\frac{25}{24}\)
y = \(\frac{7}{24}\)
Then the solution is (\(\frac{25}{24}\), \(\frac{7}{24}\)), and the triple is 7, 24, 25.
Question 7.
Use a calculator to verify that you found a Pythagorean triple in each of the Problems 4–6. Show your work.
Answer:
For the triple 77, 36, 85:
772 + 362 = 852
5929 + 1296 = 7225
7225 = 7225
For the triple 13, 84, 85:
132 + 842 = 852
169 + 7056 = 7225
7225 = 7225
For the triple 7, 24, 25:
72 + 242 = 252
49 + 576 = 625
625 = 625
Eureka Math Grade 8 Module 4 Lesson 31 Exit Ticket Answer Key
Use a calculator to complete Problems 1–3.
Question 1.
Is 7, 20, 21 a Pythagorean triple? Is 1, \(\frac{15}{8}\), \(\frac{17}{8}\) a Pythagorean triple? Explain.
Answer:
The set of numbers 7, 20, 21 is not a Pythagorean triple because 72 + 202 ≠ 212.
The set of numbers 1, \(\frac{15}{8}\), \(\frac{17}{8}\) is not a Pythagorean triple because the numbers \(\frac{15}{8}\) and \(\frac{17}{8}\) are not whole numbers.
But they are a triple because 12 + (\(\frac{15}{8}\))2 = (\(\frac{17}{8}\))2.
Question 2.
Identify two Pythagorean triples using the known triple 9, 40, 41.
Answer:
Answers will vary. Accept any triple that is a whole number multiple of 9, 40, 41.
Question 3.
Use the system 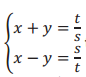 to find Pythagorean triples for the given values of s = 2 and t = 3. Recall that the solution in the form of (\(\frac{c}{b}\), \(\frac{a}{b}\)) is the triple a, b, c. Verify your results.
to find Pythagorean triples for the given values of s = 2 and t = 3. Recall that the solution in the form of (\(\frac{c}{b}\), \(\frac{a}{b}\)) is the triple a, b, c. Verify your results.
Answer:
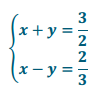
x + y + x – y = \(\frac{3}{2}\) + \(\frac{2}{3}\)
2x = \(\frac{13}{6}\)
x = \(\frac{13}{12}\)
\(\frac{13}{12}\) + y = \(\frac{3}{2}\)
y = \(\frac{3}{2}\) – \(\frac{13}{12}\)
y = \(\frac{5}{12}\)
Then the solution is (\(\frac{13}{12}\), \(\frac{5}{12}\)), and the triple is 5, 12, 13.
52 + 122 = 132
25 + 144 = 169
169 = 169