Engage NY Eureka Math 8th Grade Module 5 Lesson 10 Answer Key
Eureka Math Grade 8 Module 5 Lesson 10 Exercise Answer Key
Opening Exercise
a.
i. Write an equation to determine the volume of the rectangular prism shown below.
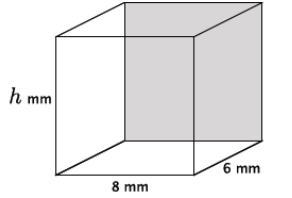
Answer:
V = 8(6)(h)
= 48h
The volume is 48h mm3.
ii. Write an equation to determine the volume of the rectangular prism shown below.
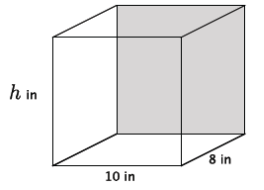
Answer:
V = 10(8)(h)
= 80h
The volume is 80h in3.
iii. Write an equation to determine the volume of the rectangular prism shown below.
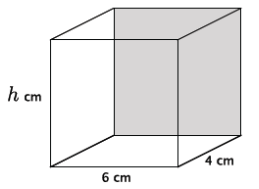
Answer:
V = 6(4)(h)
= 24h
The volume is 24h cm3.
iv. Write an equation for volume, V, in terms of the area of the base, B.
V = Bh
b. Using what you learned in part (a), write an equation to determine the volume of the cylinder shown below.
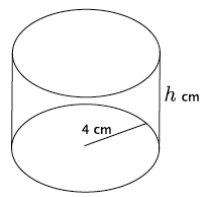
Answer:
V = Bh
= 42 πh
= 16πh
The volume is 16πh cm3.
Exercises 1–3
Exercise 1.
Use the diagram to the right to answer the questions.
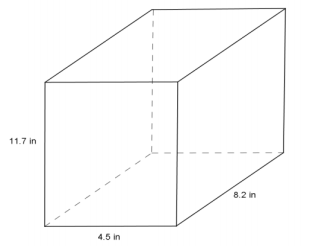
a. What is the area of the base?
Answer:
The area of the base is (4.5)(8.2) in2 or 36.9 in2.
b. What is the height?
Answer:
The height of the rectangular prism is 11.7 in.
c. What is the volume of the rectangular prism?
Answer:
The volume of the rectangular prism is 431.73 in3.
Exercise 2.
Use the diagram to the right to answer the questions.
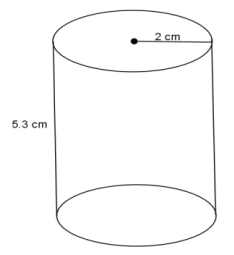
a. What is the area of the base?
Answer:
A = π22
A = 4π
The area of the base is 4π cm2.
b. What is the height?
Answer:
The height of the right circular cylinder is 5.3 cm.
c. What is the volume of the right circular cylinder?
Answer:
V = (πr2)h
V = (4π)5.3
V = 21.2π
The volume of the right circular cylinder is 21.2π cm3.
Exercise 3.
Use the diagram to the right to answer the questions.
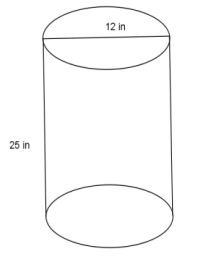
a. What is the area of the base?
Answer:
A = π62
A = 36π
The area of the base is 36π in2.
b. What is the height?
Answer:
The height of the right circular cylinder is 25 in.
c. What is the volume of the right circular cylinder?
Answer:
V = (36π)25
V = 900π
The volume of the right circular cylinder is 900π in3.
Exercises 4–6
Exercise 4.
Use the diagram to find the volume of the right circular cone.
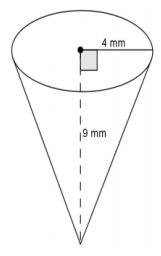
Answer:
V = \(\frac{1}{3}\) (πr2)h
V = \(\frac{1}{3}\) (π42)9
V = 48π
The volume of the right circular cone is 48π mm3.
Exercise 5.
Use the diagram to find the volume of the right circular cone.
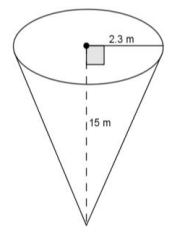
Answer:
V = \(\frac{1}{3}\) (πr2)h
V = \(\frac{1}{3}\) (π2.32)15
V = 26.45π
The volume of the right circular cone is 26.45π m3.
Exercise 6.
Challenge: A container in the shape of a right circular cone has height h, and base of radius r, as shown. It is filled with water (in its upright position) to half the height. Assume that the surface of the water is parallel to the base of the inverted cone. Use the diagram to answer the following questions:
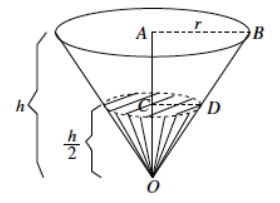
a. What do we know about the lengths of AB and AO?
Answer:
Then we know that |AB| = r, and |AO| = h.
b. What do we know about the measure of ∠OAB and ∠OCD?
Answer:
∠OAB and ∠OCD are both right angles.
c. What can you say about △OAB and △OCD?
Answer:
We have two similar triangles, △OAB and △OCD by AA criterion.
d. What is the ratio of the volume of water to the volume of the container itself?
Answer:
Since \(\frac{|A B|}{|C D|}\) = \(\frac{|A O|}{|C O|}\), and |AO| = 2|OC|, we have \(\frac{|A B|}{|C D|}\) = 2\(\frac{2|O C|}{|C O|}\).
Then |AB| = 2|CD|.
Using the volume formula to determine the volume of the container, we have V = \(\frac{1}{3}\) π|AB|2 |AO|.
By substituting |AB| with 2|CD| and |AO| with 2|OC| we get:
V = \(\frac{1}{3}\) π(2|CD|)2 (2|OC|)
V = 8(\(\frac{1}{3}\) π|CD|2 |OC|), where \(\frac{1}{3}\) π|CD|2 |OC| gives the volume of the portion of the container that is filled with water.
Therefore, the volume of the water to the volume of the container is 1:8.
Eureka Math Grade 8 Module 5 Lesson 10 Problem Set Answer Key
Question 1.
Use the diagram to help you find the volume of the right circular cylinder.
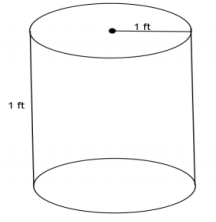
Answer:
V = πr2 h
V = π(1)2 (1)
V = π
The volume of the right circular cylinder is π ft3.
Question 2.
Use the diagram to help you find the volume of the right circular cone.
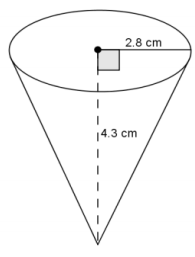
Answer:
V = \(\frac{1}{3}\) πr2 h
V = \(\frac{1}{3}\) π(2.8)2 (4.3)
V = 11.237333…π
The volume of the right circular cone is about 11.2π cm3.
Question 3.
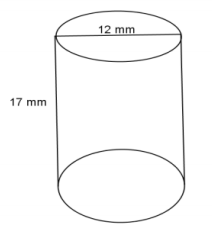
Use the diagram to help you find the volume of the right circular cylinder.
Answer:
If the diameter is 12 mm, then the radius is 6 mm.
V = πr2 h
V = π(6)2 (17)
V = 612π
The volume of the right circular cylinder is 612π mm3.
Question 4.
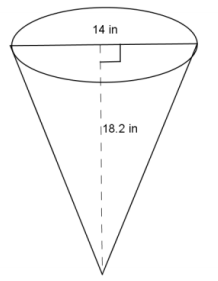
Use the diagram to help you find the volume of the right circular cone.
Answer:
If the diameter is 14 in., then the radius is 7 in.
V = \(\frac{1}{3}\) πr2 h
V = \(\frac{1}{3}\) π(7)2 (18.2)
V = 297.26666…π
V ≈ 297.3π
The volume of the right cone is about 297.3π in3.
Question 5.
Oscar wants to fill with water a bucket that is the shape of a right circular cylinder. It has a 6-inch radius and 12-inch height. He uses a shovel that has the shape of a right circular cone with a 3-inch radius and 4-inch height. How many shovelfuls will it take Oscar to fill the bucket up level with the top?
Answer:
V = πr2 h
V = π(6)2 (12)
V = 432π
The volume of the bucket is 432π in3.
V = \(\frac{1}{3}\) πr2 h
V = \(\frac{1}{3}\) π(3)2 (4)
V = 12π
The volume of shovel is 12π in3.
\(\frac{432 \pi}{12 \pi}\) = 36
It would take 36 shovelfuls of water to fill up the bucket.
Question 6.
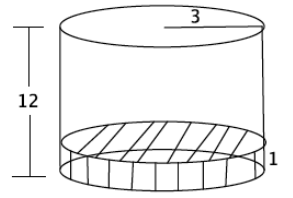
A cylindrical tank (with dimensions shown below) contains water that is 1-foot deep. If water is poured into the tank at a constant rate of 20 \(\frac{\mathrm{ft}^{3}}{\mathrm{~min}}\) for 20 min., will the tank overflow? Use 3.14 to estimate π.
Answer:
V = πr2 h
V = π(3)2 (12)
V = 108π
The volume of the tank is about 339.12 ft3.
V = πr2 h
V = π(3)2 (1)
V = 9π
There is about 28.26 ft3 of water already in the tank. There is about 310.86 ft3 of space left in the tank. If the water is poured at a constant rate for 20 min., 400 ft3 will be poured into the tank, and the tank will overflow.
Eureka Math Grade 8 Module 5 Lesson 10 Exit Ticket Answer Key
Question 1.
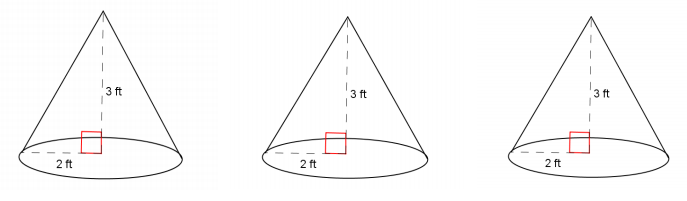
Use the diagram to find the total volume of the three cones shown below.
Answer:
Since all three cones have the same base and height, the volume of the three cones will be the same as finding the volume of a cylinder with the same base radius and same height.
V = πr2 h
V = π(2)23
V = 12π
The volume of all three cones is 12π ft3.
Question 2.
Use the diagram below to determine which has the greater volume, the cone or the cylinder.
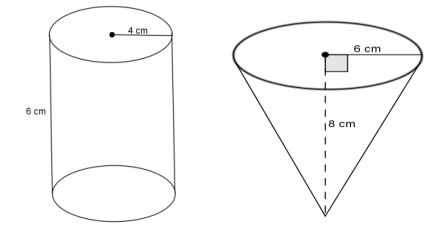
Answer:
V = πr2 h
V = π42 (6)
V = 96π
The volume of the cylinder is 96π cm3.
V = \(\frac{1}{3}\) πr2 h
V = \(\frac{1}{3}\) π62 (8)
V = 96π
The volume of the cone is 96π cm3.
The volume of the cylinder and the volume of the cone are the same, 96π cm3.