Engage NY Eureka Math 8th Grade Module 7 Lesson 14 Answer Key
Eureka Math Grade 8 Module 7 Lesson 14 Exercise Answer Key
Opening Exercise
a. Write an equation for the area, A, of the circle shown.
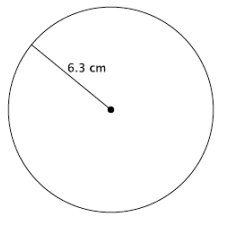
Answer:
A < π(6.3) 2
< 39.69π
The area of the circle is 39.69π cm 2 .
b. Write an equation for the circumference, C, of the circle shown.

Answer:
C < 2π(9.7)
< 19.4π
The circumference of the circle is 19.4π mm.
c. Each of the squares in the grid below has an area of 1 unit 2 .
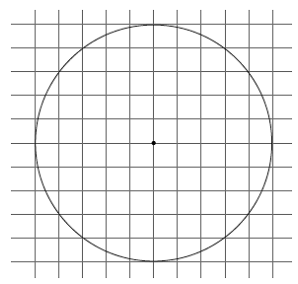
i. Estimate the area of the circle shown by counting squares.
Answer:
Estimates will vary. The approximate area of the circle is 78 units 2 .
ii. Calculate the area of the circle using a radius of 5 units. Use 3.14 as an approximation for π.
Answer:
A≈3.14(5) 2
≈78.5
The area of the circle is approximately 78.5 units 2 .
Exercises 1–4
Exercise 1.
Gerald and Sarah are building a wheel with a radius of 6.5 cm and are trying to determine the circumference. Gerald says, “Because 6.5 × 2 × 3.14 < 40.82, the circumference is 40.82 cm.” Sarah says, “Because
6.5 × 2 × 3.10 < 40.3 and 6.5 × 2 × 3.21 < 41.73, the circumference is somewhere between 40.3 and 41.73.” Explain the thinking of each student.
Answer:
Gerald is using a common approximation for the number π to determine the circumference of the wheel. That is why he used 3.14 in his calculation. Sarah is using an interval between which the value of π falls, based on the work we did in class. We know that 3.10 < π < 3.21; therefore, her calculations of the circumference uses numbers we know π to be between.
Exercise 2.
Estimate the value of the number (6.12486…) 2 .
Answer:
6.12486 2 < (6.12486…) 2 < 6.12487 2
37.5139100196 < (6.12486…) 2 < 37.5140325169
(6.12486…) 2 < 37.51 is correct up to two decimal digits.
Exercise 3.
Estimate the value of the number (9.204107…) < sup>2 < /sup>.
Answer:
9.204107 2 < (9.204107… ) 2 < 9.204108 2
84.715585667449 < (9.204107…) 2 < 84.715604075664
(9.20410…) 2 < 84.715 is correct up to three decimal digits.
Exercise 4.
Estimate the value of the number (4.014325…) < sup>2 < /sup>.
Answer:
4.014325 2 < (4.014325…) 2 < 4.014326 2
16.114805205625 < (4.014325…) 2 < 16.114813234276
(4.014325…) 2 < 16.1148 is correct up to four decimal digits.
Eureka Math Grade 8 Module 7 Lesson 14 Problem Set Answer Key
Question 1.
Caitlin estimated π to be 3.10 < π < 3.21. If she uses this approximation of π to determine the area of a circle with a radius of 5 cm, what could the area be?
Answer:
The area of the circle with radius 5 cm will be between 77.5 cm2 and 80.25 cm2.
Question 2.
Myka estimated the circumference of a circle with a radius of 4.5 in. to be 28.44 in. What approximate value of π did she use? Is it an acceptable approximation of π? Explain.
Answer:
C < 2πr
28.44 < 2π(4.5)
28.44 < 9π
\(\frac{28.44}{9}\) < π
3.16 < π
Myka used 3.16 to approximate π. Student responses may vary with respect to whether or not 3.16 is an acceptable approximation for π. Accept any reasonable explanation.
Question 3.
A length of ribbon is being cut to decorate a cylindrical cookie jar. The ribbon must be cut to a length that stretches the length of the circumference of the jar. There is only enough ribbon to make one cut. When approximating π to calculate the circumference of the jar, which number in the interval 3.10 < π < 3.21 should be used? Explain.
Answer:
In order to make sure the ribbon is long enough, we should use an estimate of π that is closer to 3.21. We know that 3.10 is a fair estimate of π but less than the actual value of π. Similarly, we know that 3.21 is a fair estimate of π but greater than the actual value of π. Since we can only make one cut, we should cut the ribbon so that there is a little more than we need, not less than. For that reason, an approximation of π closer to 3.21 should be used.
Question 4.
Estimate the value of the number (1.86211…)2.
Answer:
1.862112 < (1.86211…)2 < 1.862122
3.4674536521 < (1.86211…)2 < 3.4674908944
(1.86211…)2 < 3.4674 is correct up to four decimal digits.
Question 5.
Estimate the value of the number (5.9035687…)2.
Answer:
5.90356872 < (5.9035687…)2 < 5.90356882
34.85212339561969 < (5.9035687…)2 < 34.85212457633344
(5.9035687…)2 < 34.85212 is correct up to five decimal digits.
Question 6.
Estimate the value of the number (12.30791…)2.
Answer:
12.307912 < (12.30791…)2 < 12.307922
151.4846485681 < (12.30791…)2 < 151.4848947264
(12.30791…)2 < 151.484 is correct up to three decimal digits.
Question 7.
Estimate the value of the number (0.6289731…)2.
Answer:
0.62897312 < (0.6289731…)2 < 0.62897322
0.39560716052361 < (0.6289731…)2 < 0.39560728631824
(0.6289731…)2 < 0.395607 is correct up to six decimal digits.
Question 8.
Estimate the value of the number (1.112223333…)2.
Answer:
1.1122233332 < (1.112223333…)2 < 1.1122233342
1.2370407424696289 < (1.112223333…)2 < 1.2370407446940756
(1.112223333…)2 < 1.23704074 is correct up to eight decimal digits.
Question 9.
Which number is a better estimate for π, \(\frac{22}{7}\) or 3.14? Explain.
Answer:
Allow for both answers to be correct as long as the student provides a reasonable explanation.
A sample answer might be as follows.
I think that \(\frac{22}{7}\) is a better estimate because when I find the decimal expansion, \(\frac{22}{7}\)≈3.142857…; compared to the number 3.14, \(\frac{22}{7}\) is closer to the actual value of π.
Question 10.
To how many decimal digits can you correctly estimate the value of the number (4.56789012…)2?
Answer:
4.567890122 < (4.56789012…)2 < 4.567890132
20.8656201483936144 < (1.112223333…)2 < 20.8656202397514169
(4.56789012…)2 < 20.865620 is correct up to six decimal digits.
Eureka Math Grade 8 Module 7 Lesson 14 Exit Ticket Answer Key
Question 1.
Describe how we found a decimal approximation for π.
Answer:
To make our work easier, we looked at the number of unit squares in a quarter circle that comprised its area. We started by counting just the whole number of unit squares. Then, we continued to revise our estimate of the area by looking at parts of squares specifically to see if parts could be combined to make a whole unit square. We looked at the inside and outside boundaries and said that the value of π would be between these two numbers. The inside boundary is a conservative estimate of the value of π, and the outside boundary is an overestimate of the value of π. We could continue this process with smaller squares in order to refine our estimate for the decimal approximation of π.