Engage NY Eureka Math 8th Grade Module 7 Lesson 4 Answer Key
Eureka Math Grade 8 Module 7 Lesson 4 Example Answer Key
Example 1.
Simplify the square root as much as possible.
\(\sqrt{50}\) =
Answer:
→ Is the number 50 a perfect square? Explain.
The number 50 is not a perfect square because there is no integer squared that equals 50.
→ Since 50 is not a perfect square, when we need to simplify \(\sqrt{50}\), we write the factors of the number 50 looking specifically for those that are perfect squares. What are the factors of 50?
50 = 2 × 52
Since 50 = 2 × 52, then \(\sqrt{50}\) = \(\sqrt{2 \times 5^{2}}\). We can rewrite \(\sqrt{50}\) as a product of its factors:
\(\sqrt{50}\) = \(\sqrt{2}\) × \(\sqrt{5^{2}}\).
→ Obviously, 52 is a perfect square. Therefore, \(\sqrt{5^{2}}\) = 5, so \(\sqrt{50}\) = 5 × \(\sqrt{2}\) = 5\(\sqrt{2}\). Since \(\sqrt{2}\) is not a perfect square, we leave it as it is. We have simplified this expression as much as possible because there are no other perfect square factors remaining in the square root.
→ The number \(\sqrt{50}\) is said to be in its simplified form when all perfect square factors have been simplified. Therefore, 5\(\sqrt{2}\) is the simplified form of \(\sqrt{50}\).
Now that we know \(\sqrt{50}\) can be expressed as a product of its factors, we also know that we can multiply expressions containing square roots. For example, if we are given \(\sqrt{2}\) × \(\sqrt{5^{2}}\), we can rewrite the expression as √(2 × 52 ) = \(\sqrt{50}\).
Example 2.
Simplify the square root as much as possible.
\(\sqrt{28}\) =
Answer:
→ Is the number 28 a perfect square? Explain.
The number 28 is not a perfect square because there is no integer squared that equals 28.
→ What are the factors of 28?
28 = 22 × 7
Since 28 = 22 × 7, then \(\sqrt{28}\) = \(\sqrt{2^{2} \times 7}\). We can rewrite \(\sqrt{28}\) as a product of its factors:
\(\sqrt{28}\) = \(\sqrt{2^{2}}\) × \(\sqrt{7}\).
→ Obviously, 22 is a perfect square. Therefore, \(\sqrt{2^{2}}\) = 2, and \(\sqrt{28}\) = 2 × \(\sqrt{7}\) = 2\(\sqrt{7}\). Since \(\sqrt{7}\) is not a perfect square, we leave it as it is.
→ The number \(\sqrt{28}\) is said to be in its simplified form when all perfect square factors have been simplified. Therefore, 2\(\sqrt{7}\) is the simplified form of \(\sqrt{28}\).
Example 3.
Simplify the square root as much as possible.
\(\sqrt{128}\) =
Answer:
→ In this example, students may or may not recognize 128 as 64 × 2. The work below assumes that they do not. Consider showing students the solution below, as well as this alternative solution:
\(\sqrt{128}\) = \(\sqrt{64 \times 2}\) = \(\sqrt{64}\) × \(\sqrt{2}\) = 8 × \(\sqrt{2}\) = 8\(\sqrt{2}\).
→ Is the number 128 a perfect square? Explain.
The number 128 is not a perfect square because there is no integer squared that equals 128.
→ What are the factors of 128?
128 = 27
→ Since 128 = 27, then \(\sqrt{128}\) = √(27 ). We know that we can simplify perfect squares, so we can rewrite 27 as 22 × 22 × 22 × 2 because of what we know about the laws of exponents. Then,
\(\sqrt{128}\) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\).
Each 22 is a perfect square. Therefore, \(\sqrt{128}\) = 2 × 2 × 2 × \(\sqrt{2}\) = 8\(\sqrt{2}\).
Example 4.
Simplify the square root as much as possible.
\(\sqrt{288}\) =
Answer:
In this example, students may or may not recognize 288 as 144 × 2. The work below assumes that they do not. Consider showing students the solution below, as well as this alternative solution:
\(\sqrt{288}\) = \(\sqrt{144 \times 2}\) = \(\sqrt{144}\) × \(\sqrt{2}\) = 12 × \(\sqrt{2}\) = 12\(\sqrt{2}\).
→ Is the number 288 a perfect square? Explain.
The number 288 is not a perfect square because there is no integer squared that equals 288.
→ What are the factors of 288?
288 = 25 × 32
Since 288 = 25 × 32, then \(\sqrt{288}\) = √(25 × 32 ). What do we do next?
Use the laws of exponents to rewrite 25 as 22 × 22 × 2.
→ Then, \(\sqrt{288}\) is equivalent to
\(\sqrt{288}\) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{3^{2}}\).
→ What does this simplify to?
\(\sqrt{288}\) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{3^{2}}\)) = \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{3^{2}}\) ) × \(\sqrt{2}\) = 2 × 2 × 3 × \(\sqrt{2}\) = 12\(\sqrt{2}\)
Eureka Math Grade 8 Module 7 Lesson 4 Exercise Answer Key
Opening Exercise
a.
i. What does \(\sqrt{16}\) equal?
Answer:
4
ii. What does 4 × 4 equal?
Answer:
16
iii. Does \(\sqrt{16}\) = \(\sqrt{4 \times 4}\)?
Answer:
Yes
b.
i. What does \(\sqrt{36}\) equal?
Answer:
6
ii. What does 6 × 6 equal?
Answer:
36
iii. Does \(\sqrt{36}\) = \(\sqrt{6 \times 6}\)?
Answer:
Yes
c.
i. What does \(\sqrt{121}\) equal?
Answer:
11
ii. What does 11 × 11 equal?
Answer:
121
iii. Does \(\sqrt{121}\) = \(\sqrt{11 \times 11}\)?
Yes
d.
i. What does \(\sqrt{81}\) equal?
Answer:
9
ii. What does 9 × 9 equal?
Answer:
81
iii. Does \(\sqrt{81}\) = \(\sqrt{9 \times 9}\)?
Answer:
Yes
e. Rewrite \(\sqrt{20}\) using at least one perfect square factor.
Answer:
\(\sqrt{20}\) = \(\sqrt{4 \times 5}\)
f. Rewrite \(\sqrt{28}\) using at least one perfect square factor.
Answer:
\(\sqrt{28}\) = \(\sqrt{4 \times 7}\)
Exercises 1–4
Simplify the square roots as much as possible.
Exercise 1.
\(\sqrt{18}\)
Answer:
\(\sqrt{18}\) = \(\sqrt{2 \times 3^{2}}\)
= \(\sqrt{2}\) × \(\sqrt{3^{2}}\)
= 3\(\sqrt{2}\)
Exercise 2.
\(\sqrt{44}\)
Answer:
\(\sqrt{44}\) = \(\sqrt{2^{2} \times 11}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{11}\)
= 2\(\sqrt{11}\)
Exercise 3.
\(\sqrt{169}\)
Answer:
\(\sqrt{169}\) = \(\sqrt{13^{2}}\)
= 13
Exercise 4.
\(\sqrt{75}\)
Answer:
\(\sqrt{75}\) = \(\sqrt{3 \times 5^{2}}\)
= \(\sqrt{3}\) × \(\sqrt{5^{2}}\)
= 5\(\sqrt{3}\)
Exercises 5–8
Exercise 5.
Simplify \(\sqrt{108}\).
Answer:
\(\sqrt{108}\) = \(\sqrt{2^{2} \times 3^{3}}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{3^{2}}\) × \(\sqrt{3}\)
= 2 × 3\(\sqrt{3}\)
= 6\(\sqrt{3}\)
Exercise 6.
Simplify \(\sqrt{250}\).
Answer:
\(\sqrt{250}\) = \(\sqrt{2 \times 5^{3}}\)
= \(\sqrt{2}\) × \(\sqrt{5^{2}}\) × \(\sqrt{5}\)
= 5\(\sqrt{2}\) × \(\sqrt{5}\)
= 5\(\sqrt{10}\)
Exercise 7.
Simplify \(\sqrt{200}\).
Answer:
\(\sqrt{200}\) = \(\sqrt{2^{3} \times 5^{2}}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{5^{2}}\)
= 2 × 5\(\sqrt{2}\)
= 10\(\sqrt{2}\)
Exercise 8.
Simplify \(\sqrt{504}\).
Answer:
\(\sqrt{504}\) = \(\sqrt{2^{3} \times 3^{2} \times 7}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{2}\) × \(\sqrt{3^{2}}\) × \(\sqrt{7}\)
= 2 × 3 × \(\sqrt{2}\) × \(\sqrt{7}\)
= 6\(\sqrt{14}\)
Eureka Math Grade 8 Module 7 Lesson 4 Problem Set Answer Key
Simplify each of the square roots in Problems 1–5 as much as possible.
Question 1.
\(\sqrt{98}\)
\(\sqrt{98}\) = \(\sqrt{2 \times 7^{2}}\)
= \(\sqrt{2}\) × \(\sqrt{7^{2}}\)
= 7\(\sqrt{2}\)
Question 2.
\(\sqrt{54}\)
\(\sqrt{54}\) = \(\sqrt{2 \times 3^{3}}\)
= \(\sqrt{2}\) × \(\sqrt{3}\) × \(\sqrt{3^{2}}\)
= 3\(\sqrt{6}\)
Question 3.
\(\sqrt{144}\)
\(\sqrt{144}\) = \(\sqrt{12^{2}}\)
= 12
Question 4.
\(\sqrt{512}\)
\(\sqrt{512}\) = \(\sqrt{2^{9}}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2^{2}}\) × \(\sqrt{2}\)
= 2 × 2 × 2 × 2\(\sqrt{2}\)
= 16\(\sqrt{2}\)
Question 5.
\(\sqrt{756}\)
\(\sqrt{756}\) = \(\sqrt{2^{2} \times 3^{3} \times 7}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{3^{2}}\) × \(\sqrt{3}\) × \(\sqrt{7}\)
= 2 × 3 × \(\sqrt{21}\)
= 6\(\sqrt{21}\)
Question 6.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.
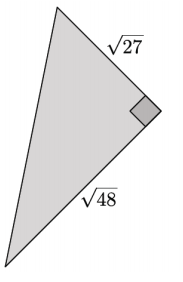
Answer:
Let c units represent the length of the hypotenuse.
(\(\sqrt{27}\))2 + (\(\sqrt{48}\))2 = c2
27 + 48 = c2
75 = c2
\(\sqrt{75}\) = \(\sqrt{c^{2}}\)
\(\sqrt{5^{2}}\) × \(\sqrt{3}\) = c
5\(\sqrt{3}\) = c
The length of the hypotenuse is 5\(\sqrt{3}\) units.
Question 7.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.
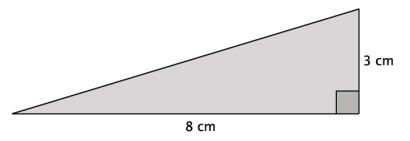
Answer:
Let c cm represent the length of the hypotenuse.
32 + 82 = c2
9 + 64 = c2
73 = c2
\(\sqrt{73}\) = \(\sqrt{c^{2}}\)
\(\sqrt{73}\) = c
The length of the unknown side is \(\sqrt{73}\) cm.
Question 8.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.
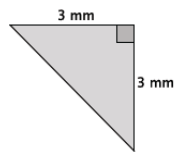
Answer:
Let c mm represent the length of the hypotenuse.
32 + 32 = c2
9 + 9 = c2
18 = c2
\(\sqrt{18}\) = \(\sqrt{c^{2}}\)
\(\sqrt{18}\) = c
\(\sqrt{3^{2}}\) × \(\sqrt{2}\) = c
3\(\sqrt{2}\) = c
The length of the unknown side is 3\(\sqrt{2}\) mm.
Question 9.
What is the length of the unknown side of the right triangle? Simplify your answer, if possible.
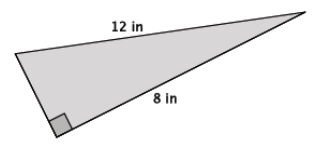
Answer:
Let x in. represent the unknown length.
x2 + 82 = 122
x2 + 64 = 144
x2 + 64 – 64 = 144 – 64
x2 = 80
\(\sqrt{x^{2}}\) = \(\sqrt{80}\)
x = \(\sqrt{80}\)
x = \(\sqrt{2^{4} \cdot 5}\)
x = \(\sqrt{2^{2}}\) ⋅ \(\sqrt{2^{2}}\) ⋅ \(\sqrt{5}\)
x = 2 ⋅ 2\(\sqrt{5}\)
x = 4\(\sqrt{5}\)
The length of the unknown side is 4\(\sqrt{5}\) in.
Question 10.
Josue simplified \(\sqrt{450}\) as 15\(\sqrt{2}\) Is he correct? Explain why or why not.
Answer:
\(\sqrt{450}\) = \(\sqrt{2 \times 3^{2} \times 5^{2}}\)
= \(\sqrt{2}\) × \(\sqrt{3^{2}}\) × \(\sqrt{5^{2}}\)
= 3 × 5 × \(\sqrt{1}\)
= 15\(\sqrt{1}\)
Yes, Josue is correct because the number 450 = 2 × 32 × 52. The factors that are perfect squares simplify to 15 leaving just the factor of 2 that cannot be simplified. Therefore, \(\sqrt{450}\) = 15\(\sqrt{2}\).
Question 11.
Tiah was absent from school the day that you learned how to simplify a square root. Using \(\sqrt{360}\), write Tiah an explanation for simplifying square roots.
Answer:
To simplify \(\sqrt{360}\), first write the factors of 360. The number 360 = 23 × 32 × 5. Now, we can use the factors to write \(\sqrt{360}\) = \(\sqrt{2^{3} \times 3^{2} \times 5}\)), which can then be expressed as \(\sqrt{360}\) = \(\sqrt{2^{3}}\) × \(\sqrt{3^{2}}\) × \(\sqrt{5}\). Because we want to simplify square roots, we can rewrite the factor \(\sqrt{2^{3}}\) as \(\sqrt{2^{2}}\) × \(\sqrt{2}\) because of the laws of exponents. Now, we have
\(\sqrt{360}\) = \(\sqrt{2^{2}}\) × √2 × \(\sqrt{3^{2}}\) × \(\sqrt{5}\).
Each perfect square can be simplified as follows:
\(\sqrt{360}\) = 2 × \(\sqrt{2}\) × 3 × \(\sqrt{5}\)
= 2 × 3 × \(\sqrt{2}\) × \(\sqrt{5}\)
= 6\(\sqrt{10}\).
The simplified version of \(\sqrt{360}\) = 6\(\sqrt{10}\).
Eureka Math Grade 8 Module 7 Lesson 4 Exit Ticket Answer Key
Simplify the square roots as much as possible.
Question 1.
\(\sqrt{24}\)
Answer:
\(\sqrt{24}\) = \(\sqrt{2^{2} \times 6}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{6}\)
= 2\(\sqrt{6}\)
Question 2.
\(\sqrt{338}\)
Answer:
\(\sqrt{338}\) = \(\sqrt{13^{2} \times 2}\)
= \(\sqrt{13^{2}}\) × \(\sqrt{24}\)
= 13\(\sqrt{2}\)
Question 3.
\(\sqrt{196}\)
Answer:
\(\sqrt{196}\) = \(\sqrt{14^{2}}\)
= 14
Question 4.
\(\sqrt{2420}\)
Answer:
\(\sqrt{2420}\) = \(\sqrt{2^{2} \times 11^{2} \times 5}\)
= \(\sqrt{2^{2}}\) × \(\sqrt{11^{2}}\) × \(\sqrt{5}\)
= 2 × 11 × \(\sqrt{5}\)
= 22\(\sqrt{5}\)