Engage NY Eureka Math 8th Grade Module 7 Lesson 7 Answer Key
Eureka Math Grade 8 Module 7 Lesson 7 Example Answer Key
Example 1.
The number 0.253 is represented on the number line below.
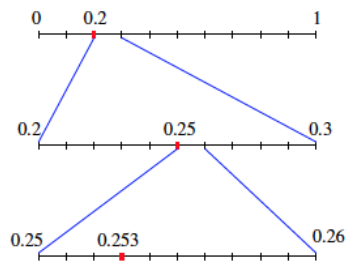
Answer:
How can we locate the number 0.253 = \(\frac{2}{10}\) + \(\frac{5}{100}\) + \(\frac{3}{1000}\) on the number line?
We can see that 0.253 is a tad larger than 0.2 and is smaller than 0.3. So if we divide the line segment from 0 to 1 into tenths, 0.253 lies somewhere in the segment between 0.2 and 0.3.
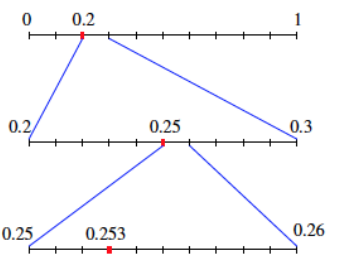
Now divide this segment into ten equal parts. (Those parts are hundredths of the original unit length.) We know that 0.253 is larger than 0.25 but smaller than 0.26, and so lies in the segment between these two values.
Now divide this small segment into tenths again. (We are now dealing with thousandths of the original unit length.) We can now see where exactly to pin 0.253 on the number line.
Writing 0.253 in its expanded decimal form of \(\frac{2}{10}\) + \(\frac{5}{100}\) + \(\frac{3}{1000}\) illustrates this process:
The first decimal digit of 0.253 is 0.2, or \(\frac{2}{10}\), and this tells us within which tenth we are to place 0.253.
The first two decimal digits of 0.253 are 0.25 which is equal to \(\frac{2}{10}\) + \(\frac{5}{10^{2}}\) , or \(\frac{25}{10^{2}}\), and this tells us within which hundredth we are to place 0.253.
The first three decimal digits of 0.253 are 0.253 which is equal to \(\frac{2}{10}\) + \(\frac{5}{10^{2}}\) + \(\frac{3}{10^{3}}\), or \(\frac{253}{10^{3}}\), and this tells us within which thousandth we are to place 0.253. And since the decimal terminates here, we are done.
Have the students explain this process again in their own words, referring to the number line diagram as they do so.
How do you think this process would change if we tried to locate an infinite decimal on the number line?
The sequence for an infinite decimal would never end; it would go on infinitely.
We need to introduce some notation. If a decimal has a repeating pattern, as for 0.3333… or 7.45454545…, for instance, then a horizontal bar is used to indicate that a block of digits is being repeated. For example, 0.3333… is written as \(0 . \overline{3}\) and 7.45454545… as \(7 . \overline{45}\). It is conceivable that an infinite decimal could have no repeating pattern.
Example 2.
The number \(\frac{5}{6}\), which is equal to 0.833333…, or \(0 . \overline{83}\) is partially represented on the number line below.
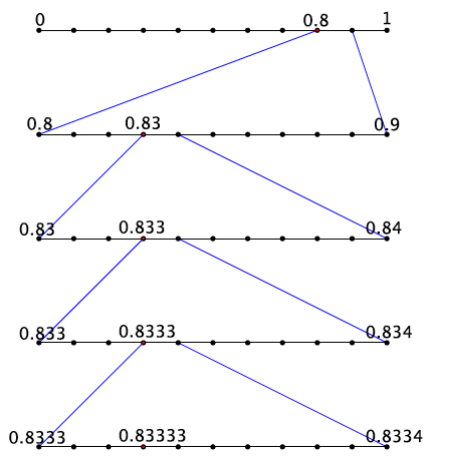
Answer:
Now, consider the equality \(\frac{5}{6}\) = 0.833333″…” = \(0 . \overline{83}\). Notice that at the second step, the work feels as though it repeats, which coincides with the fact that the decimal digit of 3 repeats.
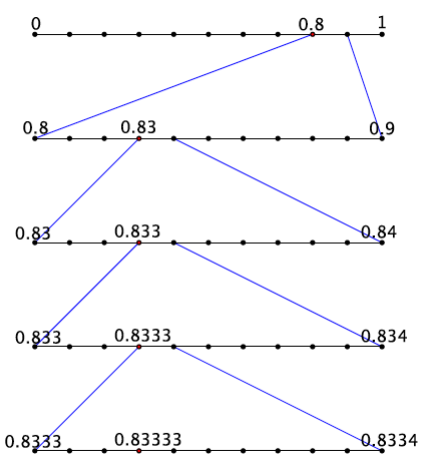
What is the expanded form of the decimal 0.833333…?
0.833333″…” = \(\frac{8}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}} + \frac{3}{10^{5}} + \frac{3}{10^{6}} + \cdots\) + …………
We see again that at the second step the work begins to repeat.
Each step can be represented by increasing powers of 10 in the denominator: \(\frac{8}{10}, \frac{83}{10^{2}}, \frac{833}{10^{3}}, \frac{8333}{10^{4}}, \frac{83333}{10^{5}}, \frac{833333}{10^{6}}\), and so on. When will it end? Explain.
It will never end because the decimal is infinite.
As we step through this process we are pinning the exact location of 0.8333… into smaller and smaller intervals, intervals with sizes shrinking to zero: an interval of a tenth, and then a hundredth, then a thousandth, and, if we kept going, an interval of size \(\frac{1}{10^{20}}\), and later on to an interval of size \(\frac{1}{10^{100}}\), and so on, supposedly forever!
Okay. Let’s now think deeply about 0.9999…. Where do we find this number on the number line?
Draw on the board a sequence of number-line segments akin to those in Example 2, and have students give instructions on how to pin down the location of 0.9999…. In which tenth does it lie? In which hundredth? In which thousandth? And so on. Ask: At any stage of this process is 0.9999… right at the number 1 on the number line?
No. We are always just to the left of 1.
Right. And that makes sense as 0.9 is smaller than 1, and 0.99 is smaller than 1, as are 0.999 and 0.9999. At every stage of the process we are just shy of the number 1.
Eureka Math Grade 8 Module 7 Lesson 7 Exercise Answer Key
Opening Exercise
a. Write the expanded form of the decimal 0.3765 using powers of 10.
Answer:
0.3765 = \(\frac{3}{10} + \frac{7}{10^{2}} + \frac{6}{10^{3}} + \frac{5}{10^{4}}\)
b. Write the expanded form of the decimal 0.3333333… using powers of 10.
Answer:
0.333333″…” = \(\frac{3}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}} + \frac{3}{10^{5}} + \frac{3}{10^{6}} + \cdots\)
c. Have you ever wondered about the value of 0.99999…? Some people say this infinite decimal has a value of 1. Some disagree. What do you think?
Answer:
Answers will vary. Have a brief discussion with students about this exercise. The answer will be revisited in the discussion below.
Exercises 1–5
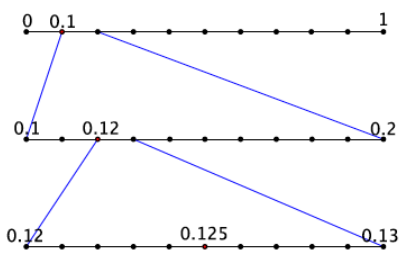
Exercise 1.
a. Write the expanded form of the decimal 0.125 using powers of 10.
Answer:
0.125 = \(\frac{1}{10} + \frac{2}{10^{2}} + \frac{5}{10^{3}}\)
b. Show on the number line the placement of the decimal 0.125.
Answer:
Exercise 2.
a. Write the expanded form of the decimal 0.3875 using powers of 10.
Answer:
0.3875 = \(\frac{3}{10} + \frac{8}{10^{2}} + \frac{7}{10^{3}} + \frac{5}{10^{4}}\)
b. Show on the number line the placement of the decimal 0.3875.
Answer:
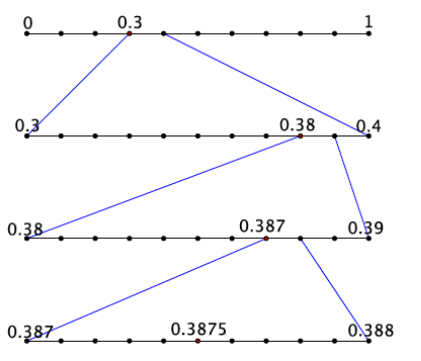
Exercise 3.
a. Write the expanded form of the decimal 0.777777… using powers of 10.
Answer:
0.777777… = \(\frac{7}{10} + \frac{7}{10^{2}} + \frac{7}{10^{3}} + \frac{7}{10^{4}} + \frac{7}{10^{5}} + \frac{7}{10^{6}} + \cdots\)
b. Show the first few stages of placing the decimal 0.777777… on the number line.
Answer:
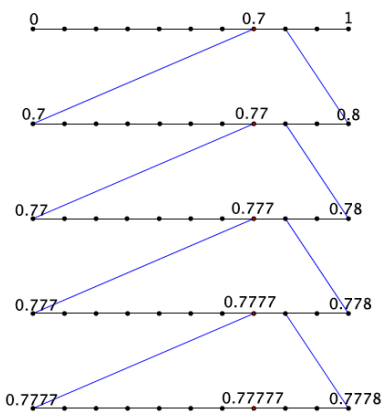
Exercise 4.
a. Write the expanded form of the decimal \(0 . \overline{45}\) using powers of 10.
Answer:
\(0 . \overline{45}\) = \(\frac{4}{10} + \frac{5}{10^{2}} + \frac{4}{10^{3}} + \frac{5}{10^{4}} + \frac{4}{10^{5}} + \frac{5}{10^{6}} + \cdots\)
b. Show the first few stages of placing the decimal \(0 . \overline{45}\) on the number line.
Answer:
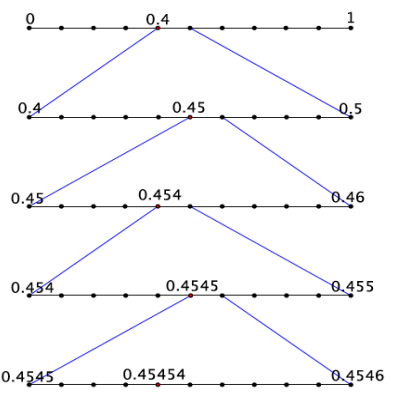
Exercise 5.
a. Order the following numbers from least to greatest: 2.121212, 2.1, 2.2, and \(2 . \overline{12}\).
Answer:
2.1, 2.121212, \(2 . \overline{12}\), and 2.2
b. Explain how you knew which order to put the numbers in.
Answer:
Each number is the sum of the whole number 2 and a decimal. When you write each number in this manner, you get the following expansions.
2.121212 = 2 + \(\frac{1}{10} + \frac{2}{10^{2}} + \frac{1}{10^{3}} + \frac{2}{10^{4}} + \frac{1}{10^{5}} + \frac{2}{10^{6}}\)
2.1 = 2 + \(\frac{1}{10}\)
2.2 = 2 + \(\frac{2}{10}\)
\(2 . \overline{12}\) = 2 + \(\frac{1}{10} + \frac{2}{10^{2}} + \frac{1}{10^{3}} + \frac{2}{10^{4}} + \frac{1}{10^{5}} + \frac{2}{10^{6}} + \frac{1}{10^{7}} + \frac{2}{10^{8}} + \cdots\)
In this form, it is clear that 2.1 is the least of the four numbers, followed by the finite decimal 2.121212, then the infinite decimal \(2 . \overline{12}\), and finally 2.2.
Eureka Math Grade 8 Module 7 Lesson 7 Problem Set Answer Key
Question 1.
a. Write the expanded form of the decimal 0.625 using powers of 10.
Answer:
0.625 = \(\frac{6}{10} + \frac{2}{10^{2}} + \frac{5}{10^{3}}\)
b. Place the decimal 0.625 on the number line.
Answer:
Question 2.
a. Write the expanded form of the decimal \(0 . \overline{370}\) using powers of 10.
Answer:
\(0 . \overline{370}\) = \(\frac{3}{10} + \frac{7}{10^{2}} + \frac{0}{10^{3}} + \frac{3}{10^{4}} + \frac{7}{10^{5}} + \frac{0}{10^{6}} + \cdots\)
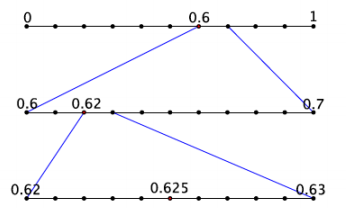
b. Show the first few stages of placing the decimal 0.370370… on the number line.
Answer:
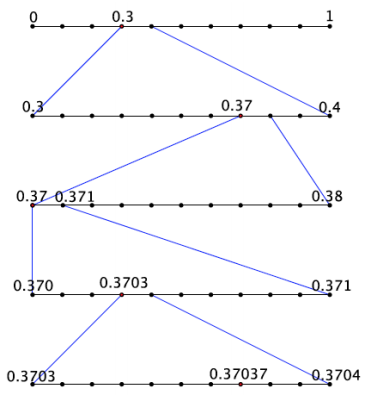
Question 3.
Which is a more accurate representation of the fraction \(\frac{2}{3}\): 0.6666 or \(0 . \overline{6}\)? Explain. Which would you prefer to compute with?
Answer:
The number \(\frac{2}{3}\) is more accurately represented by the decimal 0.6 ̅ compared to 0.6666. The long division algorithm with \(\frac{2}{3}\) shows that the digit 6 repeats. Then, the expanded form of the decimal \(0 . \overline{6}\) is \(\frac{6}{10} + \frac{6}{10^{2}} + \frac{6}{10^{3}} + \frac{6}{10^{4}} + \frac{6}{10^{5}} + \frac{6}{10^{6}} + \cdots\), and the expanded form of the decimal 0.6666 is \(\frac{6}{10} + \frac{6}{10^{2}} + \frac{6}{10^{3}} + \frac{6}{10^{4}}\). For this reason, \(0 . \overline{6}\) is precise, but 0.6666 is an approximation. For computations, I would prefer to use 0.6666. My answer would be less precise, but at least I would be able to compute with it. When attempting to compute with an infinite number, you would never finish writing it; thus, you could never compute with it.
Question 4.
Explain why we shorten infinite decimals to finite decimals to perform operations. Explain the effect of shortening an infinite decimal on our answers.
Answer:
We often shorten infinite decimals to finite decimals to perform operations because it would be impossible to represent an infinite decimal precisely since the sequence that describes infinite decimals has an infinite number of steps. Our answers are less precise; however, they are not that much less precise because with each additional digit we include in the sequence, we are adding a very small amount to the value of the number. The more decimals we include, the closer the value we add approaches zero. Therefore, it does not make that much of a difference with respect to our answer.
Question 5.
A classmate missed the discussion about why \(0 . \overline{9}\) = 1. Convince your classmate that this equality is true.
Answer:
Answers will vary. Accept any reasonable explanation. One is provided below.
Ask: Could there be any space between the locations of 0.9999… and 1 on the number line? We have that 0.9999… is larger than 0.9 and so is within one-tenth of 1 on the number line. We also have that 0.9999… is larger than 0.99 and so is within one-hundredth of 1 on the number line. And 0.9999… is larger than 0.999 and so is within one-thousandth of 1 on the number line, and so on. There can be no space between 0.9999… and 1 on the number line, as we can always argue that 0.9999… must be within any given distance from 1. Thus, 0.9999… and 1 must sit at the same location on the number line and so are the same number.
Question 6.
Explain why 0.3333 < 0.33333.
Answer:
0.3333 = \(\frac{3}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}}\), and 0.33333 = \(\frac{3}{10} + \frac{3}{10^{2}} + \frac{3}{10^{3}} + \frac{3}{10^{4}} + \frac{3}{10^{5}}\). That means that 0.33333 is exactly \(\frac{3}{10^{5}}\) larger than 0.3333. If we examined the numbers on the number line, 0.33333 is to the right of 0.3333, meaning that it is larger than 0.3333.
Eureka Math Grade 8 Module 7 Lesson 7 Exit Ticket Answer Key
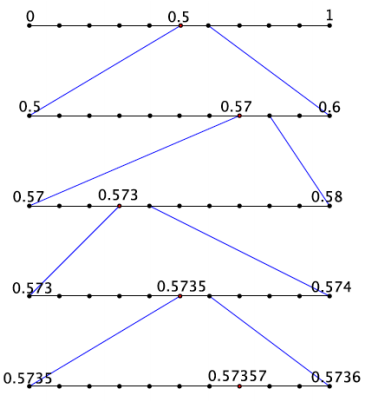
Question 1.
a. Write the expanded form of the decimal 0.829 using powers of 10.
Answer:
0.829 = \(\frac{8}{10} + \frac{2}{10^{2}} + \frac{9}{10^{3}}\)
b. Show the placement of the decimal 0.829 on the number line.
Answer:
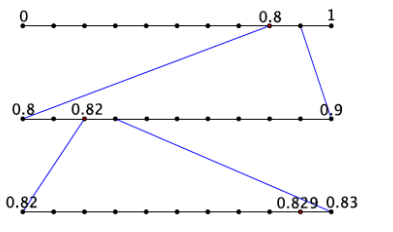
Question 2.
a. Write the expanded form of the decimal 0.55555… using powers of 10.
Answer:
0.55555″…” = \(\frac{5}{10} + \frac{5}{10^{2}} + \frac{5}{10^{3}} + \frac{5}{10^{4}} + \frac{5}{10^{5}} + \frac{5}{10^{6}} + \cdots\)
b. Show the first few stages of placing the decimal 0.555555… on the number line.
Answer:
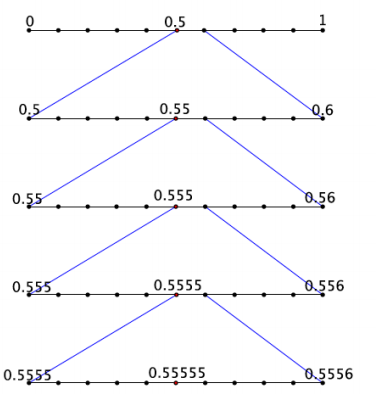
Question 3.
a. Write the expanded form of the decimal \(0 . \overline{573}\) using powers of 10.
Answer:
\(0 . \overline{573}\) = \(\frac{5}{10} + \frac{7}{10^{2}} + \frac{3}{10^{3}} + \frac{5}{10^{4}} + \frac{7}{10^{5}} + \frac{3}{10^{6}} + \cdots\)
b. Show the first few stages of placing the decimal \(0 . \overline{573}\) on the number line.
Answer: