Eureka Math Precalculus Module 2 Lesson 12 Answer Key

Engage NY Eureka Math Precalculus Module 2 Lesson 12 Answer Key

Eureka Math Precalculus Module 2 Lesson 12 Example Answer Key

Example
In three-dimensional space, let A represent a rotation of 90° about the x-axis, B represent a reflection about the
yz-plane, and C represent a rotation of 180° about the z-axis. Let X=\(\left[\begin{array}{l}
1 \\
1 \\
1
\end{array}\right]\).
a. As best you can, sketch a three-dimensional set of axes and the location of the point X.
Answer:

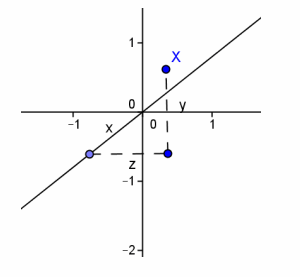
b. Using only your geometric intuition, what are the coordinates of BX? CX? Explain your thinking.
Answer:
BX=\(\left[\begin{array}{l}
-1 \\
1 \\
1
\end{array}\right]\); CX=\(\left[\begin{array}{l}
-1 \\
-1 \\
1
\end{array}\right]\); answers will vary but could include that when rotating about the x-axis 90°, only the x-coordinate would change signs; however, when rotating about the z-axis 180°, the x- and
y-coordinates would change signs.

c. Write down matrices B and C, and verify or disprove your answers to part (b).
Answer:

d. What is the sum of BX+CX?
Answer:
BX+CX=\(\left[\begin{array}{c}
-2 \\
0 \\
2
\end{array}\right]\)

e. Write down matrix A, and compute A(BX+CX).
Answer:

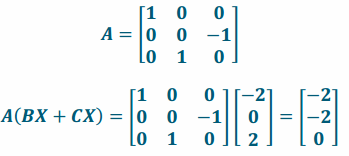
f. Compute AB and AC.
Answer:

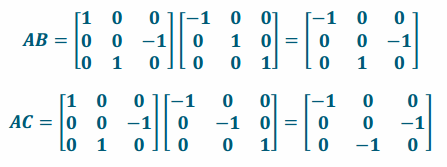
g. Compute (AB)X, (AC)X, and their sum. Compare your result to your answer to part (e). What do you notice?
Answer:

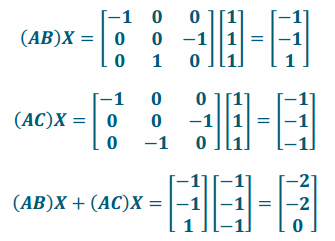
A(BX+CX)=(AB)X+(AC)X

h. In general, must A(B+C) and AB+AC have the same geometric effect on a point, no matter what matrices A, B, and C are? Explain.
Answer:
Yes. See full explanation in questions above.

Eureka Math Precalculus Module 2 Lesson 12 Exercise Answer Key

Opening Exercise
Write the 3×3 matrix that would represent the transformation listed.
a. No change when multiplying (the multiplicative identity matrix)
Answer:
\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)

b. No change when adding (the additive identity matrix)
Answer:
\(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]\)

c. A rotation about the x-axis of θ degrees
Answer:
\(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos (\theta) & -\sin (\theta) \\
0 & \sin (\theta) & \cos (\theta)
\end{array}\right]\)

d. A rotation about the y-axis of θ degrees
Answer:
\(\left[\begin{array}{ccc}
\cos (\theta) & 0 & \sin (\theta) \\
0 & 1 & 0 \\
-\sin (\theta) & 0 & \cos (\theta)
\end{array}\right]\)

e. A rotation about the z-axis of θ degrees
Answer:
\(\left[\begin{array}{ccc}
\cos (\theta) & -\sin (\theta) & 0 \\
\sin (\theta) & \cos (\theta & 0 \\
0 & 0 & 1
\end{array}\right]\)

f. A reflection over the xy-plane
Answer:
\(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right]\)

g. A reflection over the yz-plane
Answer:
\(\left[\begin{array}{ccc}
-1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)

h. A reflection over the xz-plane
Answer:
\(\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & 1
\end{array}\right]\)

i. A reflection over y=x in the xy-plane
Answer:
\(\left[\begin{array}{lll}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right]\)

Exercises

Exercise 1.
Let A=\(\left[\begin{array}{ll}
x & z \\
y & w
\end{array}\right]\), B=\(\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\), and C=\(\left[\begin{array}{ll}
e & g \\
f & h
\end{array}\right]\).
a. Write down the products AB, AC, and A(B+C).
Answer:

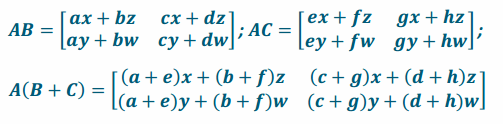
b. Verify that A(B+C)=AB+AC.
Answer:

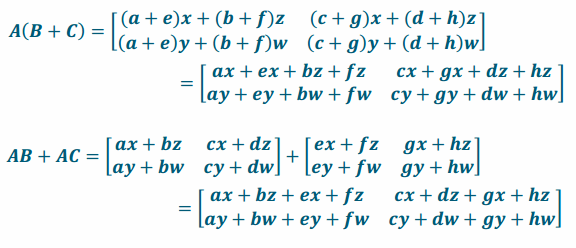
Therefore, A(B+C)=AB+AC.

Exercise 2.
Suppose A, B, and C are 3×3 matrices and X is a point in three-dimensional space.
a. Explain why the point (A(BC))X must be the same point as ((AB)C)X.
Answer:
(A(BC))X=(A)(B)(C)X. Applying BC and then A is the same as applying C, then B, and then A.
(A)(B)(C)X=((AB)C)X. Applying C, then B, and then A is the same as applying C and then AB.

b. Explain why matrix multiplication must be associative.
Answer:
Matrix multiplication is associative because performing the transformation B and then A on a point X is the same as applying the product of AB to point X.

c. Verify using the matrices from Exercise 1 that A(BC)=(AB)C.
Answer:

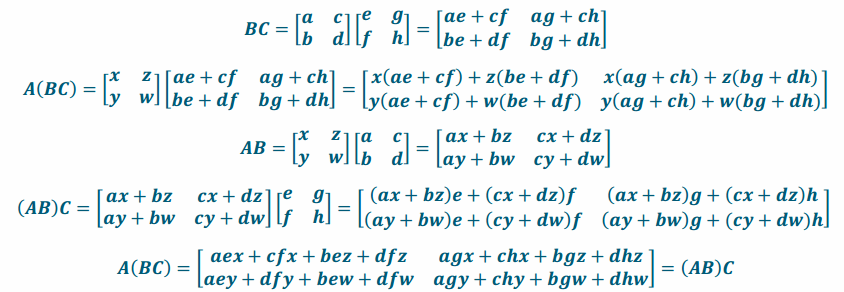
Eureka Math Precalculus Module 2 Lesson 12 Problem Set Answer Key

Question 1.
Let matrix A=\(\left(\begin{array}{cc}
3 & -2 \\
-1 & 0
\end{array}\right)\), matrix B=\(\left(\begin{array}{ll}
4 & 4 \\
3 & 9
\end{array}\right)\), and matrix C=\(\left(\begin{array}{cc}
8 & 2 \\
7 & -5
\end{array}\right)\). Calculate the following:
a. AB
Answer:
\(\left(\begin{array}{cc}
6 & -6 \\
-4 & -4
\end{array}\right)\)

b. AC
Answer:
\(\left(\begin{array}{cc}
10 & 16 \\
-8 & -2
\end{array}\right)\)

c. A(B+C)
Answer:

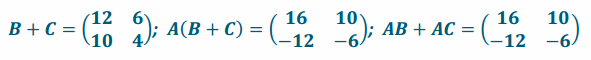
We have that A(B+C)=AB+AC.

d. AB+AC
Answer:
\(\left(\begin{array}{cc}
16 & 10 \\
-12 & -6
\end{array}\right)\)

e. (A+B)C
Answer:
(A+B)C=AC+BC, so BC has not been calculated yet. We get
BC=\(\left(\begin{array}{ll}
60 & -12 \\
87 & -39
\end{array}\right)\).
So,
(A+B)C=\(\left(\begin{array}{cc}
70 & 4 \\
79 & -41
\end{array}\right)\).

f. A(BC)
Answer:
A(BC)=A\(\left(\begin{array}{ll}
60 & -12 \\
87 & -39
\end{array}\right)\)
=\(\left(\begin{array}{cc}
6 & 42 \\
-60 & 12
\end{array}\right)\)

Question 2.
Apply each of the transformations you found in Problem 1 to the points x=\(\left(\begin{array}{l}
1 \\
1
\end{array}\right)\), y=\(\left(\begin{array}{l}
-3 \\
2
\end{array}\right)\), and x+y.
Answer:
a. (AB)x=\(\left(\begin{array}{c}
\mathbf{0} \\
-8
\end{array}\right)\)
(AB)y=\(\left(\begin{array}{c}
-30 \\
4
\end{array}\right)\)
(AB)(x+y)=\(\left(\begin{array}{c}
-30 \\
-4
\end{array}\right)\)

b. (AC)x=\(\left(\begin{array}{c}
26 \\
-10
\end{array}\right)\)
(AC)y=\(\left(\begin{array}{c}
2 \\
20
\end{array}\right)\)
(AC)(x+y)=\(\left(\begin{array}{c}
28 \\
10
\end{array}\right)\)

c. (A(B+C))x=\(\left(\begin{array}{c}
26 \\
-18
\end{array}\right)\)
(A(B+C))y=\(\left(\begin{array}{c}
-28 \\
24
\end{array}\right)\)
(A(B+C))(x+y)=\(\left(\begin{array}{c}
-2 \\
6
\end{array}\right)\)

d. Same as part (c)
(AB+AC)x=\(\left(\begin{array}{c}
26 \\
-18
\end{array}\right)\)
(AB+AC)y=\(\left(\begin{array}{c}
-28 \\
24
\end{array}\right)\)
(AB+AC)(x+y)=\(\left(\begin{array}{c}
-2 \\
6
\end{array}\right)\)

e. ((A+B)C)x=\(\left(\begin{array}{c}
74 \\
38
\end{array}\right)\)
((A+B)C)y=\(\left(\begin{array}{c}
-202 \\
-319
\end{array}\right)\)
((A+B)C)(x+y)=\(\left(\begin{array}{c}
-128 \\
-281
\end{array}\right)\)

f. (A(BC))x=\(\left(\begin{array}{c}
48 \\
-48
\end{array}\right)\)
(A(BC))y=\(\left(\begin{array}{c}
66 \\
204
\end{array}\right)\)
(A(BC))(x+y)=\(\left(\begin{array}{c}
114 \\
156
\end{array}\right)\)

Question 3.
Let A, B, C, and D be any four square matrices of the same dimensions. Use the distributive property to evaluate the following:
a. (A+B)(C+D)
Answer:
(A+B)C+(A+B)D=AC+BC+AD+BD

b. (A+B)(A+B)
Answer:
AA+AB+BA+BB

c. What conditions need to be true for part (b) to equal AA+2AB+BB?
Answer:
AB=BA needs to be true.

Question 4.
Let A be a 2×2 matrix and B, C be the scalar matrices B=\(\left(\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right)\), and C=\(\left(\begin{array}{ll}
3 & 0 \\
0 & 3
\end{array}\right)\). Answer the following questions.
a. Evaluate the following:
i. BC
Answer:
\(\left(\begin{array}{ll}
6 & 0 \\
0 & 6
\end{array}\right)\)

ii. CB
Answer:
\(\left(\begin{array}{ll}
6 & 0 \\
0 & 6
\end{array}\right)\)

iii. B+C
Answer:
\(\left(\begin{array}{ll}
5 & 0 \\
0 & 5
\end{array}\right)\)

iv. B-C
Answer:
\(\left(\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right)\)

b. Are your answers to part (a) what you expected? Why or why not?
Answer:
Answers may vary. Students should expect that the matrices behave like real numbers since they represent scalars.

c. Let A=\(\left(\begin{array}{ll}
x & y \\
z & w
\end{array}\right)\); does AB=BA? Does AC=CA?
Answer:
Yes, AB=\(\left(\begin{array}{cc}
2 x & 2 y \\
2 z & 2 w
\end{array}\right)\)=BA, and AC=\(\left(\begin{array}{cc}
3 x & 3 y \\
3 z & 3 w
\end{array}\right)\)=CA.

d. What is (A+B)(A+C)? Write the matrix A with the letter and not in matrix form. How does this compare to (x+2)(x+3)?
Answer:
(A+B)(A+C)=AA+BA+AC+BC
=AA+2A+3A+\(\left(\begin{array}{ll}
6 & 0 \\
0 & 6
\end{array}\right)\)
=AA+5A+\(\left(\begin{array}{ll}
6 & 0 \\
0 & 6
\end{array}\right)\)
This is identical to (x+2)(x+3), with x=A.

e. With B and C given as above, is it possible to factor AA-A-BC?
Answer:
Yes. We need factors of -BC that add to -1. It looks like B and -C work, so we get (A+B)(A-C).

Question 5.
Define the sum of any two functions with the same domain to be the function f+g such that for each x in the domain of f and g, (f+g)(x)=f(x)+g(x). Define the product of any two functions to be the function fg, such that for each x in the domain of f and g, (fg)(x)=(f(x))(g(x)).
Let f, g, and h be real-valued functions defined by the equations f(x)=3x+1, g(x)=-\(\frac{1}{2}\) x+2, and
h(x)=x²-4.

a. Does f(g+h)=fg+fh?
Answer:
Yes. If we can show that (f(g+h))(x)=(fg)(x)+(fh)(x), then we will have shown that the functions are equal to each other.
(f(g+h))(x)=(f(x))((g+h)(x))
=(3x+1)(-\(\frac{1}{2}\) x+2+x²-4)
=(3x+1)((-\(\frac{1}{2}\) x+2)+(x²-4))
=(3x+1)(-\(\frac{1}{2}\) x+2)+(3x+1)(x²-4)
=(f(x))(g(x))+(f(x))(h(x))
=(fg)(x)+(fh)(x)

b. Show that this is true for any three functions with the same domains.
Answer:
(f(g+h))(x)=(f(x))((g+h)(x))
=(f(x))(g(x)+h(x))
=(f(x))(g(x))+(f(x))(h(x))
=(fg)(x)+(fh)(x)

c. Does f∘(g+h)=f∘g+f∘h for the functions described above?
Answer:
No
(f∘(g+h))(x)=f(-\(\frac{1}{2}\) x+2+x²-4)
=3⋅(-\(\frac{1}{2}\) x+2+x²-4)+1
=3⋅(-\(\frac{1}{2}\) x+2)+3⋅(x²-4)+1
The addition by 1 prevented it from working. If f(x) would have been a proportion, then the composition would have worked.

Eureka Math Precalculus Module 2 Lesson 12 Exit Ticket Answer Key

In three-dimensional space, matrix A represents a 180° rotation about the y-axis, matrix B represents a reflection about the xz-plane, and matrix C represents a reflection about the xy-plane. Answer the following:
a. Write matrices A, B, and C.
Answer:

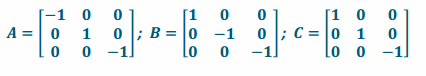
b. If X=\(\left[\begin{array}{l}
2 \\
2 \\
2
\end{array}\right]\), compute A(BX+CX).
Answer:

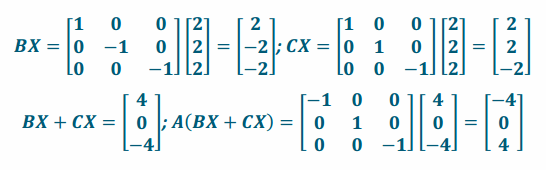
c. What matrix operations are equivalent to A(BX+CX)? What property is shown?
Answer:
A(BX+CX)=(AB)X+(AC)X; matrix multiplication is distributive.

d. Would (A(BC))X=((AB)C)X? Why?
Answer:
Yes; matrix multiplication is associative.