Engage NY Eureka Math Precalculus Module 3 End of Module Assessment Answer Key
Eureka Math Precalculus Module 3 End of Module Assessment Task Answer Key
Question 1.
Let C be the function that assigns to a temperature given in degrees Fahrenheit its equivalent in degrees Celsius, and let K be the function that assigns to a temperature given in degrees Celsius its equivalent in degrees Kelvin.
We have C(x) = \(\frac{5}{9}\) (x – 32) and K(x) = x + 273.
a. Write an expression for K(C(x)) and interpret its meaning in terms of temperatures.
Answer:
K (C (x )) = C (x ) + 273 = \(\frac{5}{9}\) (x – 32 ) + 273 . This shows the arithmetic needed to convert a temperature given in Fahrenheit to its equivalent in Kelvin.
b. The following shows the graph of y = C(x).
According to the graph, what is the value of C – 1 (95)?
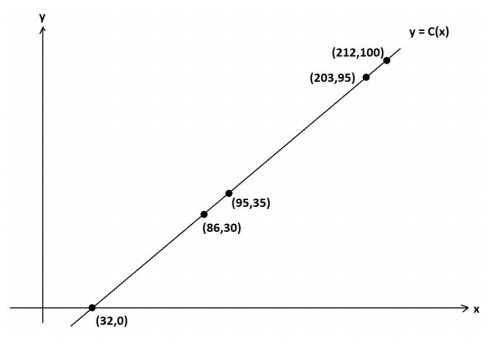
Answer:
We see that C (203 ) = 95; so, C-1 (95 ) = 203.
c. Show that C – 1 (x) = \(\frac{9}{5}\) x + 32.
Answer:
If y = \(\frac{5}{9}\) (x – 32) , then x = \(\frac{9}{5}\) y + 32 . This shows that C-1 (x ) = \(\frac{9}{5}\) x + 32 .
OR
Let d be the function given by d (x ) = \(\frac{9}{5}\) x + 32 . Then
C (d (x )) = C (\(\frac{9}{5}\) x + 32 ) = \(\frac{5}{9}\) ((\(\frac{9}{5}\) x + 32 ) – 32 ) = \(\frac{5}{9}\) ∙ \(\frac{9}{5}\) x = x
and
d (C (x )) = d (\(\frac{5}{9}\) (x – 32 )) = \(\frac{9}{5}\) (\(\frac{5}{9}\) (x – 32 )) + 32 = (x – 32 ) + 32 = x ,
which show that d is indeed the inverse function to C .
A weather balloon rises vertically directly above a station at the North Pole. Its height at time t minutes is H(t) = \(\frac{500}{2^{t}}\) meters. A gauge on the balloon measures atmospheric temperature in degrees Celsius.
Also, let T be the function that assigns to a value y the temperature, measured in Kelvin, of the atmosphere y meters directly above the North Pole on the day and hour the weather balloon is launched. (Assume that the temperature profile of the atmosphere is stable during the balloon flight.)
d. At a certain time t minutes, K – 1 (T(H(t))) = – 20. What is the readout on the temperature gauge on the balloon at this time?
Answer:
T(H (t )) is the temperature of the atmosphere, in Kelvin, at height H(t) , and K-1 (T (H (t ))) is this temperature converted to Celsius, which now matches the gauge. So if K-1 (T (H (t ))) = –20 , then the readout on the gauge is –20 .
e. Find, to one decimal place, the value of H – 1 (300) = – 20, and interpret its meaning.
Answer:
Now 300 = 500 – \(\frac{500}{2^{t}}\) if \(\frac{500}{2^{t}}\) = 200 , that is 2t = \(\frac{5}{2}\). This means t log (2) = log(\(\frac{5}{2}\)) ; so,
t = \(\frac{\log \left(\frac{5}{2}\right)}{\log (2)}\) ≈ 1.3 minutes. Thus, H-1 (300) ≈ 1.3 . This is the time, in minutes, at which the balloon is at a height of 300 meters.
Question 2.
Let f and g be the functions defined by f(x) = \(10^{\frac{x + 2}{3}}\) and g(x) = log(\(\frac{x^{3}}{100}\)) for all positive real numbers, x. (Here the logarithm is a base – ten logarithm.)
Verify by composition that f and g are inverse functions to each other.
Answer:
Consider f (g (x )) for a positive real number x . We have
f (g (x )) = 10\(\frac{\log \left(\frac{x^{3}}{1-O 0}\right)+2}{3}\) = ( 10\(\))\(\frac{1}{3}\) ∙ 10 \(\frac{2}{3}\)
= (\(\frac{x^{3}}{100}\) )\(\frac{1}{3}\) ∙ 10\(\frac{2}{3}\)
= \(\frac{x}{100^{\frac{1}{3}}}\) ∙ 10\(\frac{2}{3}\)
= \(\frac{x}{10^{2}}\) ∙ 10\(\frac{2}{3}\) = x.
And we also have
g (f (x )) = log (\(\frac{\left(10^{\frac{x+2}{3}}\right)^{3}}{100}\)) = log (\(\frac{10^{x+2}}{100}\)) = log (\(\frac{100 \cdot 10^{x}}{100}\)) = log (10x) = x .
Thus, f and g are inverse functions to each other.
Question 3.
Water from a leaky faucet is dripping into a bucket. Its rate of flow is not steady, but it is always positive. The bucket is large enough to contain all the water that will flow from the faucet over any given hour.
The table below shows V, the total amount of water in the bucket, measured in cubic centimeters, as a function of time t, measured in minutes, since the bucket was first placed under the faucet.

a. Explain why V is an invertible function.
Answer:
The volume in the bucket is always increasing. So for a given volume (in the range of volumes suitable for this context), there is only one time at which the volume of water in the bucket is that volume. That is, from a given value of the volume, we can determine a unique matching time for that volume. The function V is thus invertible.
b. Find V – 1(63.2), and interpret its meaning in the context of this situation.
Answer:
From the table we see that V (5 ) = 63.2 ; so, V-1 (63.2 ) = 5 . The time at which there were 63.2 cubic centimeters of water in the bucket was 5 minutes.
Question 4.
a. Draw a sketch of the graph of y = \(\frac{1}{x}\).
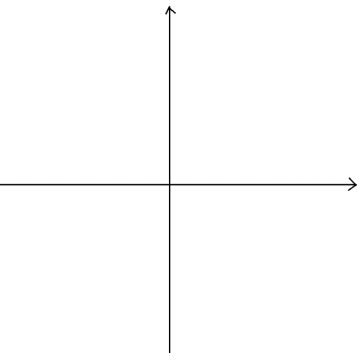
Answer:
b. Sketch the graph of y = \(\frac{x}{x – 1}\), being sure to indicate its vertical and horizontal asymptotes.
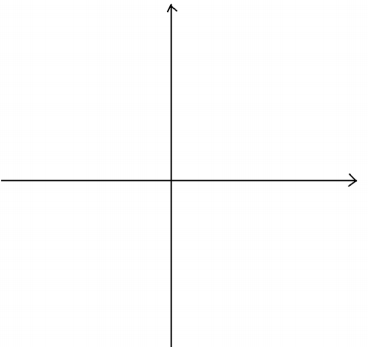
Answer:
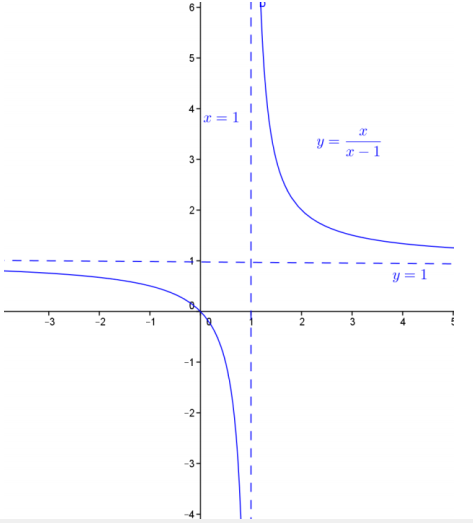
Let f be the function defined by f(x) = \(\frac{x}{x – 1}\) for all real values x different from 1.
c. Find f(f(x)) for x, a real number different from 1. What can you conclude about f – 1 (x)?
Answer:
Suppose x is a real number different from 1 .
f (f (x )) = f (\(\frac{x}{x-1}\)) = \(\frac{\frac{x}{x-1}}{\frac{x}{x-1}-1}\)
= \(\frac{x}{x-1(x-1)}\)
= \(\frac{x}{x-x+1}\)
= x
This shows that the function f itself is the inverse of the function f . We have
f -1 (x ) = f (x ) = \(\frac{x}{x-1}\)
NOTE: Notice that if x is in the domain of f (i.e., it is a real number different from 1 ), then f(x) is again a real number different from 1 and so is in the domain of f . We are thus permitted to write f(f(x)) .
Question 5.
Let f be the function given by f(x) = x2 + 3.
a. Explain why f is not an invertible function on the domain of all real numbers.
Answer:
f (–7 ) = f(7) = 52 , for example, shows that some outputs come from more than one input for this function. The function is not invertible.
b. Describe a set S of real numbers such that if we restrict the domain of f to S, the function f has an inverse function. Be sure to explain why f has an inverse for your chosen set S.
Answer:
We need to choose a set of real numbers S over which the function is strictly increasing or strictly decreasing.
Let’s choose S to be the set of all nonpositive real numbers.
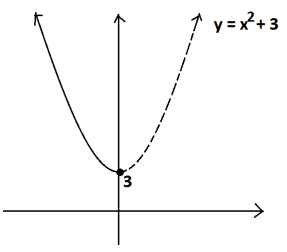
Now, the range of f is the set of all real values greater than or equal to 3 . If y is a value in this range, we see from the graph that there is only one nonpositive value x such that f(x) = y . Thus, f has an inverse function if we restrict f to the set of nonpositive inputs.
NOTE: Many answers are possible. For example, S could be the set of all positive real numbers, or the set of all real numbers just between –10 and –2 , or the set consisting of the number –3 and all the real numbers greater than 3 , for example.
Question 6.
The graph of y = x + 3 is shown below.
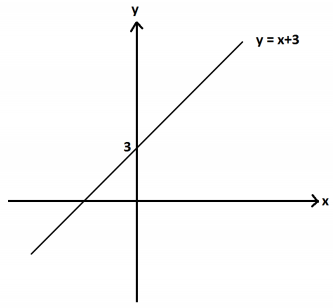
Consider the rational function h given by h(x) = \(\frac{x^{2} – x – 12}{x – 4}\).
Simon argues that the graph of y = h(x) is identical to the graph of y = x + 3. Is Simon correct? If so, how does one reach this conclusion? If not, what is the correct graph of y = h(x)? Explain your reasoning throughout.
Answer:
h (x ) = \(\frac{x^{2}-x-12}{x-4}\) is defined for all values x different from 4 .
If x is indeed different from 4 , we have
\(\frac{x^{2}-x-12}{x-4}\) = \(\frac{(x+3)(x-4)}{x-4}\) = x + 3 .
(Dividing the numerator and denominator each by x – 4 is valid as this is a nonzero quantity in the case of x ≠ 4 .)
So we see that h (x ) = 
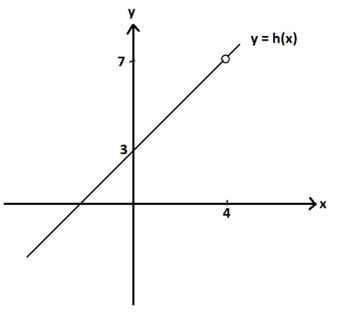
The graph of y = h(x) is shown on the right.
Question 7.
Let f be the function given by f(x) = 2x for all real values x, and let g be the function given by g(x) = log2(x) for positive real values x.
a. Sketch a graph of y = f(g(x)). Describe any restrictions on the domain and range of the functions and the composite functions.
Answer:
f (g (x )) is meaningful if x is an appropriate input for g , that is, a positive real number, and its output, g(x) , is an appropriate input for f (which it shall be, as all real values are appropriate inputs for f ). Thus, f0g is defined only for positive real inputs.
If x is a positive real number, then f (g (x )) = 2log2x = x , as exponential functions and logarithmic functions (with matching bases) are inverse functions. The graph of y = f(g (x )) is shown on the right.
b. Sketch a graph of y = g(f(x)). Describe any restrictions on the domain and range of the functions and the composite functions.
Answer:
g(f (x )) is meaningful if x is an appropriate input for f , which is the case for all real values x , and its output, f(x) , is an appropriate input for g , which it shall be as 2x is a positive value. Thus, g0f is defined only for all real inputs.
If x is a real number, then g(f (x )) = logx(2x) = x as exponential functions and logarithmic functions (with matching bases) are inverse functions. Thus, the graph of y = g(f (x )) is as shown on the right.
Question 8.
Let f be the rational function given by f(x) = \(\frac{x + 2}{x – 1}\) and g be the rational function given by g(x) = \(\frac{x – 2}{x + 1}\).
a. Write f(x) ÷ g(x) as a rational expression.
Answer:
f(x) ÷ g(x) = \(\frac{x+2}{x-1}\) ÷ \(\frac{x-2}{x+1}\) = \(\frac{(x+2)(x+1)}{(x-1)(x-2)}\)
b. Write f(x) + g(x) as a rational expression.
Answer:
f(x) + g(x) = \(\frac{x+2}{x-1}\) + \(\frac{x-2}{x+1}\) = \(\frac{(x+2)(x+1)+(x-2)(x-1)}{(x-1)(x+1)^{m}}\) = \(\frac{2 x^{2}+4}{x^{2}-1}\)
c. Write f(x) – g(x) as a rational expression.
Answer:
f(x) – g(x) = \(\frac{x+2}{x-1}\) – \(\frac{x-2}{x+1}\) = \(\frac{(x+2)(x+1)-(x-2)(x-1)}{(x-1)(x+1)}\) = \(\frac{6 x}{x^{2}-1}\)
d. Write \(\frac{2 f(x)}{f(x) + g(x)}\) as a rational expression.
Answer:
We have \(\frac{2 f(x)}{f(x) + g(x)}\) = 2(\(\frac{x+2}{x-1}\)) ÷ (\(\frac{2 x^{2}+4}{x^{2}-1}\)) = \(\frac{2(x+2)\left(x^{2}-1\right)}{(x-1)\left(2 x^{2}+4\right)}\) = \(\frac{2(x+2)(x-1)(x+1)}{(x-1) \cdot 2\left(x^{2}+2\right)}\) = \(\frac{(x+2)(x+1)}{x^{2}+2}\)
e. Ronaldo says that f is the inverse function to g. Is he correct? How do you know?
Answer:
We have, for example, f (2 ) = \(\frac{4}{1}\) = 4 but g (4 ) = \(\frac{2}{3}\). That is, g (f (2 )) is not 2 . If f were the inverse function to g , then we should see g (f (2 )) = 2 . Ronaldo is not correct.
f. Daphne says that the graph of f and the graph of g each have the same horizontal line as a horizontal asymptote. Is she correct? How do you know?
Answer:
We have f (x ) = \(\frac{x+2}{x-1}\) = \(\frac{x\left(1+\frac{2}{x}\right)}{x\left(1-\frac{1}{x}\right)}\). If x is a real number large in magnitude, then \(\frac{2}{x}\) and \(\frac{1}{x}\) each have values close to zero, and, in this case, f (x ) ≈ \(\frac{1+0}{1-0}\) = 1 shows that the graph of f has the horizontal line y = 1 as an asymptote.
The same work shows that g (x ) = \(\frac{x\left(1-\frac{2}{x}\right)}{x\left(1+\frac{1}{x}\right)}\) also has the line y = 1 as a horizontal asymptote.
Thus, Daphne is indeed correct.
Let r(x) = f(x)∙g(x), and consider the graph of y = r(x).
g. What are the x – intercepts of the graph of y = r(x)?
Answer:
For y = r (x ) = \(\frac{(x+2)(x-2)}{(x+1)(x-1)}\), we have y = 0 when x = –2 and x = 2 . The x-intercepts occur at the points (–2, 0) and (2, 0) .
h. What is the y – intercept of y = r(x)?
Answer:
r (0 ) = \(\frac{(2)(-2)}{(1)(-1)}\) = 4 . The y-intercept occurs at the point (0, 4) .
i. At which x – values is r(x) undefined?
Answer:
r(x) is undefined at x = 1 and at x = –1 .
j. Does the graph of y = r(x) have a horizontal asymptote? Explain your reasoning.
Answer:
We have
y = r (x ) = \(\frac{x^{2}-4}{x^{2}-1}\) = \(\frac{x^{2}\left(1-\frac{4}{x^{2}}\right)}{x^{2}\left(1-\frac{1}{x^{2}}\right)}\).
If x is a real positive number or a real negative number large in magnitude (and so certainly not zero), then
r (x ) = \(\frac{1-\frac{4}{x^{2}}}{1-\frac{1}{x^{2}}}\) ≈ \(\frac{1-0}{1-0}\) = 1 .
This shows that the graph of y = r(x) closely matches the horizontal line y = 1 for large positive and large negative inputs. We have a horizontal asymptote, the line y = 1 .
Notice that for values of x large in magnitude, x2 – 1 and x2 – 4 are positive, and
\(\frac{x^{2}-4}{x^{2}-1}\) < \(\frac{x^{2}-1}{x^{2}-1}\) < 1 , so the graph of y = r(x) always lies below its horizontal asymptote in its long-term behavior.
k. Give a sketch of the graph of y = r(x) which shows the broad features you identified in parts (g)–(j).
Answer:
The broad features of the graph are indicated as so, with the dashed lines representing asymptotes:
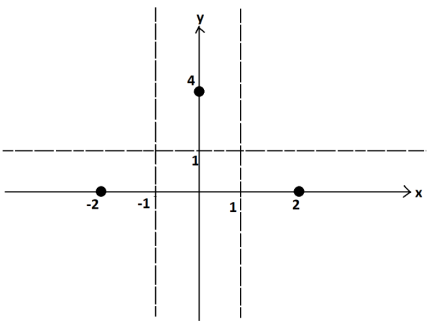
Given the graph of y = r(x) crosses the x-axis only at x = –2 and x = 2 and the y-axis only at y = 4 , we deduce that the graph of the curve can only be of the form:
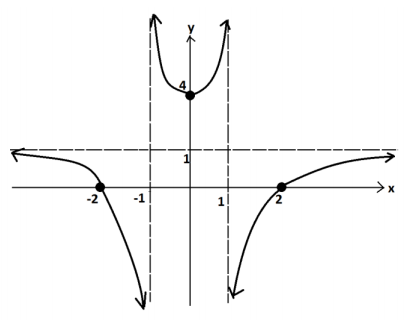
Question 9.
An algae growth in an aquarium triples in mass every two days. The mass of algae was 2.5 grams on June 21, considered day zero, and the following table shows the mass of the algae on later days.

Let m(d) represent the mass of the algae, in grams, on day d. Thus, we are regarding m as a function of time given in units of days. Our time measurements need not remain whole numbers. (We can work with fractions of days too, for example.)
a. Explain why m is an invertible function of time.
Answer:
The algae grows in mass over time, so its mass is an increasing function of time. For each possible value of mass (output), there is only one possible time (input) at which the growth has that mass. Thus, we can define an inverse function.
b. According to the table, what is the value of m – 1 (202.5)? Interpret its meaning in the context of this situation.
Answer:
m-1 (202.5) represents the number of days required for the algae to attain a mass of 202.5 grams. According to the table, we have m-1 (202.5 ) = 8 days.
c. Find a formula for the inverse function m, and use your formula to find the value of m – 1 (400) to one decimal place.
Answer:
The growth is exponential. The initial mass is 2.5 grams, and the mass triples every two days. We see that m (d ) = 2.5 ∙ 3\(\frac{d}{2}\). To find the inverse function to m , notice that
If y = 2.5 ∙ 3\(\frac{d}{2}\), then
log (y ) = log (2.5 ) + \(\frac{d}{2}\) log (3)
log (y ) – log (2.5 ) = \(\frac{d}{2}\) log (3)
(using base-ten logarithms) giving
d = \(\frac{2}{\log (3)}\) ( log (y ) – log (2.5)) = \(\frac{2 \log \left(\frac{y}{2,5}\right)}{\log (3)}\) .
This shows
m-1 (y ) = \(\frac{2 \log \left(\frac{y}{2.5}\right)}{\log (3)}\) .
To finish, we see
m-1 (400 ) = \(\frac{2 \log \left(\frac{y}{2.5}\right)}{\log (3)}\) ≈ 9.2 days.