Eureka Math Precalculus Module 3 Lesson 4 Answer Key

Engage NY Eureka Math Precalculus Module 3 Lesson 4 Answer Key

Eureka Math Precalculus Module 3 Lesson 4 Exercise Answer Key

Exercises
Exercise 1.
Show that z = 1 + i is a solution to the fourth degree polynomial equation z⁴ – z³ + 3z² – 4z + 6 = 0.
Answer:
If (1 + i)⁴ – (1 + i)³ + 3(1 + i)² – 4(1 + i) + 6 = 0, then z = 1 + i is a solution.
(1 + i)² = 1² + 2(i)(i) + i² = 2i
(1 + i)³ = (1 + i) (1 + i)² = (1 + i)(2i) = – 2 + 2i
(1 + i)⁴ = ((1 + i)²)² = (2i)² = 4i² = – 4
(1 + i)⁴ – (1 + i)³ + 3(1 + i)² – 4(1 + i) + 6 = – 4 – ( – 2 + 2i) + 3(2i) – 4(1 + i) + 6
= – 4 + 2 – 2i + 6i – 4 – 4i + 6
= 0

Exercise 2.
Show that z = 1 – i is a solution to the fourth degree polynomial equation z⁴ – z³ + 3z² – 4z + 6 = 0.
Answer:
If (1 – i)⁴ – (1 – i)³ + 3(1 – i)² – 4(1 – i) + 6 = 0, then z = 1 – i is a solution.
(1 – i)² = 1² + 2(1)( – i) + ( – i)² = – 2i
(1 – i)³ = (1 – i) (1 – i)² = (1 – i)( – 2i) = – 2 – 2i
(1 – i)⁴ = ((1 – i)²)² = ( – 2i)² = 4i² = – 4
(1 – i)⁴ – (1 – i)³ + 3(1 – i)² – 4(1 – i) + 6 = – 4 – ( – 2 – 2i) + 3( – 2i) – 4(1 – i) + 6
= – 4 + 2 + 2i – 6i – 4 + 4i + 6
= 0

Exercise 3.
Based on the patterns seen in Pascal’s triangle, what would be the coefficients of Rows 7 and 8 in the triangle? Write the coefficients of the triangle beneath the part of the triangle shown.

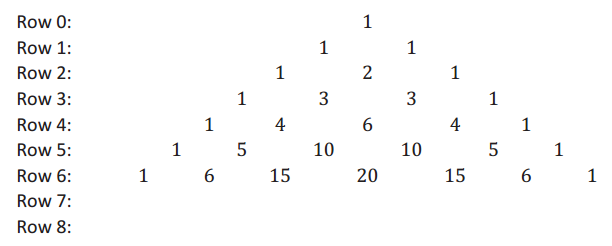
Answer:

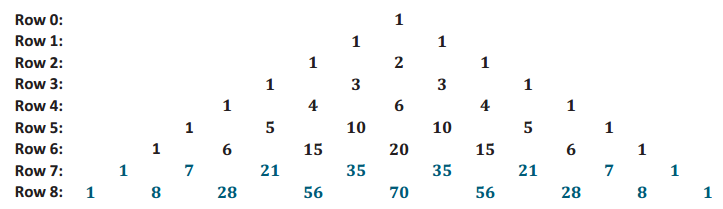
Exercise 4.
Calculate the following factorials.
a. 6!
Answer:
6! = 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 720

b. 10!
Answer:
10! = 10 ⋅ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 3 628 800

Exercise 5.
Calculate the value of the following factorial expressions.
a. \(\frac{7 !}{6 !}\)
Answer:
\(\frac{7 !}{6 !}\) = \(\frac{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\) = 7

b. \(\frac{10 !}{6 !}\)
Answer:
\(\frac{10 !}{6 !}\) = \(\frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\) = 10 9 8 7 = 5040

c. \(\frac{8 !}{5 !}\)
Answer:
\(\frac{8 !}{5 !}\) = \(\frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\) = 8 7 6 = 336

d. \(\frac{12 !}{10 !}\)
Answer:
\(\frac{12 !}{10 !}\) = \(\frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\) = 12 11 = 132

Exercise 6.
Calculate the following quantities.
a. C(1, 0) and C(1, 1)
Answer:
C(1, 0) = \(\frac{1 !}{0 ! 1 !}\) = 1 and C(1, 1) = \(\frac{1 !}{0 ! 1 !}\) = 1

b. C(2, 0), C(2, 1), and C(2, 2)
Answer:
C(2, 0) = \(\frac{2 !}{0 ! 2 !}\) = 1, C(2, 1) = \(\frac{2 !}{1 ! 1 !}\) = 2, and C(2, 2) = \(\frac{2 !}{2 ! 0 !}\) = 1

c. C(3, 0), C(3, 1), C(3, 2), and C(3, 3)
Answer:
C(3, 0) = \(\frac{3 !}{(0 ! 3 !)}\) = 1, C(3, 1) = \(\frac{3 !}{(1 ! 2 !)}\) = 3, C(3, 2) = \(\frac{3 !}{(2 ! 1 !)}\) = 3, and C(3, 3) = \(\frac{3 !}{(3 ! 0 !)}\) = 1

d. C(4, 0), C(4, 1), C(4, 2), C(4, 3), and C(4, 4)
Answer:
C(4, 0) = \(\frac{4 !}{0 ! 4 !}\) = 1, C(4, 1) = \(\frac{4 !}{1 ! 3 !}\) = 4, C(4, 2) = \(\frac{4 !}{2 ! 2 !}\) = 6, C(4, 3) = \(\frac{4 !}{3 ! 1 !}\), and C(4, 4) = \(\frac{4 !}{4 ! 0 !}\) = 1

Exercise 7.
What patterns do you see in Exercise 6?
Answer:
The numbers C(n, k) for 1≤n≤4 give the same numbers as in Pascal’s triangle.
Also, it appears that C(n, 0) = 1 and C(n, n) = 1 for each n.

Exercise 8.
Expand the expression (u + v)³.
Answer:
(u + v)³ = (u + v)(u² + 2uv + v²)
= u³ + 2u² v + uv² + vu² + 2uv² + v³
= u³ + 3u² v + 3uv² + v³

Exercise 9.
Expand the expression (u + v)⁴.
Answer:
(u + v)⁴ = (u + v)(u³ + 3u² v + 3uv² + v³)
= u⁴ + 3u³ v + 3u² v² + uv³ + vu³ + 3u² v² + 3uv³ + v⁴
= u⁴ + 4u³ v + 6u² v² + 4uv³ + v⁴

Exercise 10.
a. Multiply the expression you wrote in Exercise 9 by u.
Answer:
u(u⁴ + 4u³ v + 6u² v² + 4uv³ + v⁴) = u⁵ + 4u⁴ v + 6u³ v² + 4u² v³ + uv⁴

b. Multiply the expression you wrote in Exercise 9 by v.
Answer:
v(u⁴ + 4u³ v + 6u² v² + 4uv³ + v⁴) = u⁴ v + 4u³ v² + 6u² v³ + 4uv⁴ + v⁵

c. How can you use the results from parts (a) and (b) to find the expanded form of the expression (u + v)⁵?
Answer:
Because (u + v)⁵ = (u + v) (u + v)⁴ = u(u + v)⁴ + v(u + v)⁴, we have
(u + v)⁵ = (u⁵ + 4u⁴ v + 6u³ v² + 4u² v³ + uv⁴) + (u⁴ v + 4u³ v² + 6u² v³ + 4uv⁴ + v⁵)
= u⁵ + 5u⁴ v + 10u³ v² + 10u² v³ + 5uv⁴ + v⁵ .

Exercise 11.
What do you notice about your expansions for (u + v)⁴ and (u + v)⁵? Does your observation hold for other powers of (u + v)?
Answer:
The coefficients of (u + v)⁴ are the numbers in Row 4 of Pascal’s triangle. The coefficients of (u + v)⁵ are the numbers in Row 5 of Pascal’s triangle. The same pattern holds for (u + v), (u + v)², and (u + v)³.

Exercise 12.
Use the binomial theorem to expand the following binomial expressions.
a. (x + y)⁶
Answer:
x⁶ + 6x⁵ y + 15x⁴ y² + 20x³ y³ + 15x² y⁴ + 6xy⁵ + y⁶

b. (x + 2y)³
Answer:
x³ + 6x² y + 12xy² + 8y³

c. (ab + bc)⁴
Answer:
a⁴ b⁴ + 4a³ b⁴ c + 6a² b⁴ c² + 4ab⁴ c³ + b⁴ c⁴

d. (3xy – 2z)³
Answer:
27x³ y³ – 54x² y² z + 36xyz² – 8z³

e. (4p² qr – qr²)⁵
Answer:
1024p¹⁰ q⁵ r⁵ – 1280p⁸ q⁵ r⁶ + 640p⁶ q⁵ r⁷ – 160p⁴ q⁵ r⁸ + 20p² q⁵ r⁹ – q⁵ r¹⁰

Eureka Math Precalculus Module 3 Lesson 4 Problem Set Answer Key

Question 1.
Evaluate the following expressions.
a. \(\frac{9 !}{8 !}\)
\(\frac{9 !}{8 !}\) = \(\frac{9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\) = 9

b. \(\frac{7 !}{5 !}\)
Answer:
\(\frac{7 !}{5 !}\) = \(\frac{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\) = 7 ⋅ 6 = 42

c. \(\frac{21 !}{19 !}\)
Answer:
\(\frac{21 !}{19 !}\) = \(\frac{21 \cdot 20 \cdot 19 \cdot 18 \cdot 17 \cdots \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{19 \cdot 18 \cdot 17 \cdots \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\) = 21 ⋅ 20 = 420

d. \(\frac{8 !}{4 !}\)
Answer:
\(\frac{8 !}{4 !}\) = \(\frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{4 \cdot 3 \cdot 2 \cdot 1}\) = 8 ⋅ 7 ⋅ 6 ⋅ 5 = 1680

Question 2.
Use the binomial theorem to expand the following binomial expressions.
a. (x + y)⁴
Answer:
(x + y)⁴ = x⁴ + C(4, 1) x³ y + C(4, 2) x² y² + C(4, 3)xy³ + y⁴
= x⁴ + 4x³ y + 6x² y² + 4xy³ + y⁴

b. (x + 2y)⁴
Answer:
(x + 2y)⁴ = x⁴ + C(4, 1) x³ (2y) + C(4, 2) x² (2y)² + C(4, 3)x(2y)³ + (2y)⁴
= x⁴ + 4x³ (2y) + 6x² (4y²) + 4x(8y³) + 16y⁴
= x⁴ + 8x³ y + 24x² y² + 32xy³ + 16y⁴

c. (x + 2xy)⁴
Answer:
(x + 2xy)⁴ = x⁴ + C(4, 1) x³ (2xy) + C(4, 2) x² (2xy)² + C(4, 3)x(2xy)³ + (2xy)⁴
= x⁴ + 4x³ (2xy) + 6x² (4x² y²) + 4x(8x³ y³) + 16x⁴ y⁴
= x⁴ + 8x⁴ y + 24x⁴ y² + 32x⁴ y³ + 16x⁴ y⁴

d. (x – y)⁴
Answer:
(x – y)⁴ = (x + ( – y))⁴
= x⁴ + C(4, 1) x³ ( – y) + C(4, 2) x² ( – y)² + C(4, 3)x( – y)³ + ( – y)⁴
= x⁴ – 4x³ y + 6x² y² – 4xy³ + y⁴

e. (x – 2xy)⁴
Answer:
(x – 2xy)⁴ = x⁴ + C(4, 1) x³ ( – 2xy) + C(4, 2) x² ( – 2xy)² + C(4, 3)x( – 2xy)³ + ( – 2xy)⁴
= x⁴ + 4x³ ( – 2xy) + 6x² (4x² y²) + 4x( – 8x³ y³) + 16x⁴ y⁴
= x⁴ – 8x⁴ y + 24x⁴ y² – 32x⁴ y³ + 16x⁴ y⁴

Question 3.
Use the binomial theorem to expand the following binomial expressions.
a. (1 + \(\sqrt{2}\))⁵
Answer:
(1 + \(\sqrt{2}\))⁵ = 1⁵ + C(5, 1) 1⁴ \(\sqrt{2}\) + C(5, 2) 1³ (\(\sqrt{2}\))² + C(5, 3) 1² (\(\sqrt{2}\))³ + C(5, 4)1 ⋅ (\(\sqrt{2}\))⁴ + (\(\sqrt{2}\))⁵
= 1 + 5\(\sqrt{2}\) + 10 ⋅ 2 + 10 ⋅ 2\(\sqrt{2}\) + 5 ⋅ 4 + 4\(\sqrt{2}\)
= 41 + 29\(\sqrt{2}\)

b. (1 + i)⁹
Answer:
(1 + i)⁹ = 1 + 9i + 36i² + 84i³ + 126i⁴ + 126i⁵ + 84i⁶ + 36i⁷ + 9i⁸ + i⁹
= 1 + 9i – 36 – 84i + 126 + 126i – 84 – 36i + 9 + i
= 16 + 16i

c. (1 – π)⁵ (Hint: 1 – π = 1 + ( – π).)
Answer:
(1 – π)⁵ = 1 + C(5, 1)( – π) + C(5, 2) ( – π)² + C(5, 3) ( – π)³ + C(5, 4) ( – π)⁴ + ( – π)⁵
= 1 – 5π + 10π² – 10π³ + 5π⁴ – π⁵

d. (\(\sqrt{2}\) + i)⁶
Answer:
(\(\sqrt{2}\) + i)⁶ = (\(\sqrt{2}\))⁶ + C(6, 1) (\(\sqrt{2}\))⁵ i + C(6, 2) (\(\sqrt{2}\))⁴ i² + C(6, 3) (\(\sqrt{2}\))³ i³ + C(6, 4) (\(\sqrt{2}\))² i⁴ + C(6, 5) \(\sqrt{2}\) i⁵ + i⁶
= 8 + 6 ⋅ 4\(\sqrt{2}\) i + 15 ⋅ 4(–1) + 20 ⋅ 2\(\sqrt{2}\) ( – i) + 15 ⋅ 2 ⋅ 1 + 6\(\sqrt{2}\) (i) + ( – 1)
= – 23 – 10\(\sqrt{2}\) i

e. (2 – i)⁶
Answer:
(2 – i)⁶ = (2 + ( – i))⁶
= 2⁶ + C(6, 1) 2⁵ ( – i) + C(6, 2) 2⁴ ( – i)² + C(6, 3) 2³ ( – i)³ + C(6, 4) 2² ( – i)⁴ + C(6, 5)2( – i)⁵ + ( – i)⁶
= 64 – 6 ⋅ 32i + 15 ⋅ 16( – 1) + 20 ⋅ 8(i) + 15 ⋅ 4 ⋅ 1 + 6 ⋅ 2( – i) – 1
= – 117 – 44i

Question 4.
Consider the expansion of (a + b)¹². Determine the coefficients for the terms with the powers of a and b shown.
a. a² b¹⁰
Answer:
(a + b)¹² = a¹² + C(12, 1) a¹¹ b + ⋯ + C(12, 10) a² b¹⁰ + C(12, 11)ab¹¹ + b¹²
So, the coefficient of a² b¹⁰ is C(12, 10) = 1\(\frac{12 !}{2 ! 10 !}\) = \(\frac{12 \cdot 11}{2 \cdot 1}\) = 66.

b. a⁵ b⁷
Answer:
The coefficient of a⁵ b⁷ is C(12, 7) = \(\frac{12 !}{5 ! 7 !}\) = \(\frac{12 \cdot 11 \cdot 10 \cdot 9 \cdot 8}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\) = 792.

c. a⁸ b⁴
Answer:
The coefficient of a⁸ b⁴ is C(12, 4) = \(\frac{12 !}{8 ! 4 !}\) = \(\frac{12 \cdot 11 \cdot 10 \cdot 9}{4 \cdot 3 \cdot 2 \cdot 1}\) = 495.

Question 5.
Consider the expansion of (x + 2y)¹⁰. Determine the coefficients for the terms with the powers of x and y shown.
a. x² y⁸
Answer:
The x² y⁸ term is C(10, 8) x² (2y)⁸ = 45x² ⋅ 256y⁸ = 11520 x² y⁸, so the coefficient of x² y⁸ is 11, 520.

b. x⁴ y⁶
Answer:
The x⁴ y⁶ term is C(10, 6) x⁴ (2y)⁶ = 210x⁴ ⋅ 64y⁶ = 13440 x⁴ y⁶, so the coefficient of x⁴ y⁶ is 13, 440.

c. x⁵ y⁵
Answer:
The x⁵ y⁵ term is C(10, 5) x⁵ (2y)⁵ = 252x² ⋅ 32y⁸ = 8064 x⁵ y⁵, so the coefficient of x⁵ y⁵ is 8, 064.

Question 6.
Consider the expansion of (5p + 2q)⁶. Determine the coefficients for the terms with the powers of p and q shown.
a. p² q⁴
Answer:
Since C(6, 2) = 15 and 15(5p)² (2q)⁴ = 15(25p²)(16q⁴) = 6000p² q⁴, the coefficient is 6, 000.

b. p⁵ q
Answer:
Since C(6, 5) = 6 and 6(5p)⁵ (2q) = 6(3125p⁵)(2q) = 37500p⁵ q, the coefficient is 37, 500.

c. p³ q³
Answer:
Since C(6, 3) = 20 and 20(5p)³ (2q)³ = 20(125p³)(8q³) = 20000p³ q³, the coefficient is 20, 000.

Question 7.
Explain why the coefficient of the term that contains uⁿ is 1 in the expansion of (u + v)ⁿ.
Answer:
The corresponding binomial coefficient is C(n, 0) = \(\frac{n !}{0 ! n !}\) = \(\frac{1}{0 !}\) = 1.

Question 8.
Explain why the coefficient of the term that contains u^{(n – 1)}v is n in the expansion of (u + v)ⁿ.
Answer:
The corresponding binomial coefficient is C(n, 1) = \(\frac{n !}{1 !(n – 1) !}\) = \(\frac{n \cdot(n – 1) \cdot(n – 2) \cdots 2 \cdot 1}{(1)((n – 1) \cdot(n – 2) \cdots 2 \cdot 1)}\) = n.

Question 9.
Explain why the rows of Pascal’s triangle are symmetric. That is, explain why C(n, k) = C(n, (n – k)).
Answer:
Using the formula for the binomial coefficients, C(n, k) = \(\frac{n !}{k !(n – k) !}\) and C(n, n – k) = \(\frac{n !}{(n – k) !(n – (n – k) !)^{\prime}}\), so C(n, n – k) = \(\frac{n !}{(n – k) ! n !}\) = C(n, k).

Eureka Math Precalculus Module 3 Lesson 4 Exit Ticket Answer Key

Question 1.
Evaluate the following expressions.
a. 5!
Answer:
5! = 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120

b. \(\frac{8 !}{6 !}\)
Answer:
\(\frac{8 !}{6 !}\) = \(\frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\) = 8 ⋅ 7 = 56

c. C(7, 3)
Answer:
C(7, 3) = \(\frac{7 !}{3 ! 4 !}\) = \(\frac{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{(3 \cdot 2 \cdot 1)(4 \cdot 3 \cdot 2 \cdot 1)}\) = \(\frac{7 \cdot 6 \cdot 5}{3 \cdot 2 \cdot 1}\) = 35
Alternatively, students could use the corresponding entry of Row 7 of Pascal’s triangle, 7 21 35 35 21 7 1, which is 35.

Question 2.
Find the coefficients of the terms below in the expansion of (u + v)⁸. Explain your reasoning.
a. u² v⁶
Answer:
The binomial theorem says that the u² v⁶ term of the expansion is C(8, 2) u² v⁶, so the coefficient is
C(8, 2) = \(\frac{8 !}{2 ! 6 !}\) = 28. Alternatively, Row 8 of Pascal’s triangle is 1 8 28 56 70 56 28 8 1, and the entry corresponding to u² v⁶ is 28.

b. u³ v⁵
Answer:
The binomial theorem says that the u³ v⁵ term of the expansion is C(8, 3) u³ v⁵, so the coefficient is
C(8, 3) = \(\frac{8 !}{3 ! 5 !}\) = 56. Alternatively, Row 8 of Pascal’s triangle is 1 8 28 56 70 56 28 8 1, and the entry corresponding to u³ v⁵ is 56.

c. u⁴ v⁴
Answer:
The binomial theorem says that the u⁴ v⁴ term of the expansion is C(8, 4)u⁴ v⁴, so the coefficient is
C(8, 4) = \(\frac{8 !}{4 ! 4 !}\) = 70. Alternatively, Row 8 of Pascal’s triangle is 1 8 28 56 70 56 28 8 1, and the entry corresponding to u⁴ v⁴ is 70.