Eureka Math Precalculus Module 4 Lesson 1 Answer Key

Engage NY Eureka Math Precalculus Module 4 Lesson 1 Answer Key

Eureka Math Precalculus Module 4 Lesson 1 Example Answer Key

Example 1.
Find the following values for the rotation θ = \(\frac{\pi}{3}\) around the carousel. Create a sketch of the situation to help you. Interpret what each value means in terms of the position of the rider.
Answer:

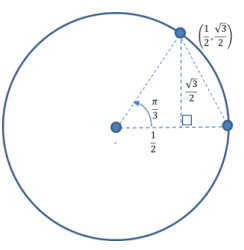
a. sin(θ)
Answer:
sin(\(\frac{\pi}{3}\)) = \(\frac{\sqrt{3}}{2}\)
For the rotation θ = \(\frac{\pi}{3}\), the rider is located \(\frac{\sqrt{3}}{2}\) units in front of the center of the carousel.

b. cos(θ)
Answer:
Based on the diagram shown in part (a), cos(\(\frac{\pi}{3}\)) = \(\frac{1}{2}\).
For the rotation θ = \(\frac{\pi}{3}\), the rider is located \(\frac{1}{2}\) unit to the right of the center of the carousel.

c. tan(θ)
Answer:
Based on the diagram shown in part (a), tan(\(\frac{\pi}{3}\)) = \(\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}\) = \(\sqrt{3}\).
For the rotation θ = \(\frac{\pi}{3}\), the ratio of the front/back position to the right/left position relative to the center of the carousel is \(\sqrt{3}\).

Example 2.
Use your understanding of the unit circle and trigonometric functions to find the values requested.
a. sin( – \(\frac{\pi}{3}\))
Answer:
sin( – \(\frac{\pi}{3}\)) = sin(2π – \(\frac{\pi}{3}\)) = – sin(\(\frac{\pi}{3}\)) = – \(\frac{\sqrt{3}}{2}\)

b. tan(\(\frac{5\pi}{4}\))
Answer:
tan(\(\frac{5\pi}{4}\)) = tan(π + \(\frac{\pi}{4}\)) = tan(\(\frac{\pi}{4}\)) = 1

Eureka Math Precalculus Module 4 Lesson 1 Exercise Answer Key

Exercise 1.
Assume that the carousel is being safety tested, and a safety mannequin is the rider. The ride is being stopped at different rotation values so technicians can check the carousel’s parts. Find the sine, cosine, and tangent for each rotation indicated, and explain how these values relate to the position of the mannequin when the carousel stops at these rotation values. Use your carousel models to help you determine the values, and sketch your model in the space provided.
a. θ = \(\frac{\pi}{4}\)
Answer:

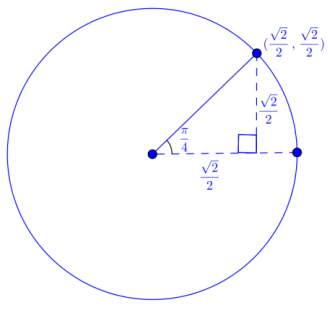
Since sin(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\), the rider is approximately \(\frac{\sqrt{2}}{2}\) units in front of the carousel’s center when it stops.
Since cos(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\), the rider is approximately \(\frac{\sqrt{2}}{2}\) units to the right of the carousel’s center when it stops.
Since tan(\(\frac{\pi}{4}\)) = (\(\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}\)) = 1, the front/back distance of the rider is equal to its right/left distance when it stops.

b. θ = \(\frac{\pi}{6}\)
Answer:

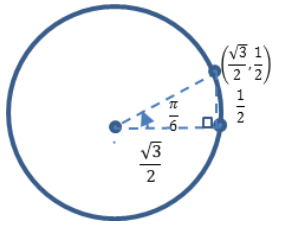
Since sin(\(\frac{\pi}{6}\)) = \(\frac{1}{2}\), the rider is approximately \(\frac{1}{2}\) unit in front of the carousel’s center when it stops.
Since cos(\(\frac{\pi}{6}\)) = \(\frac{\sqrt{3}}{2}\), the rider is approximately \(\frac{\sqrt{3}}{2}\) units to the right of the carousel’s center when it stops.
Since tan(\(\frac{\pi}{6}\)) = \(\frac{\frac{1}{2}}{\frac{\sqrt{3}}{2}}\) = \(\frac{1}{\sqrt{3}}\) = \(\frac{\sqrt{3}}{3}\), the front/back to right/left ratio of the rider is \(\frac{\sqrt{3}}{3}\) when it stops.

Exercise 2.
Use your understanding of the unit circle to determine the values of the functions shown.
a. sin(\(\frac{11\pi}{6}\))
Answer:
sin(\(\frac{11\pi}{6}\)) = sin(2π – \(\frac{\pi}{6}\)) = – sin(\(\frac{\pi}{6}\)) = – \(\frac{1}{2}\)

b. cos(\(\frac{3\pi}{4}\))
Answer:
cos(\(\frac{3\pi}{4}\)) = cos(π – \(\frac{\pi}{4}\)) = – cos(\(\frac{\pi}{4}\)) = – \(\frac{\sqrt{2}}{2}\)

c. tan( – π)
Answer:
tan⁡( – π) = tan(π + 0) = tan(0) = \(\frac{0}{1}\) = 0

Eureka Math Precalculus Module 4 Lesson 1 Problem Set Answer Key

Question 1.
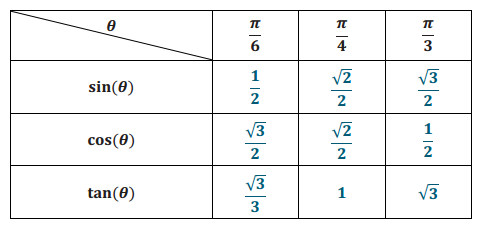
Complete the chart below.

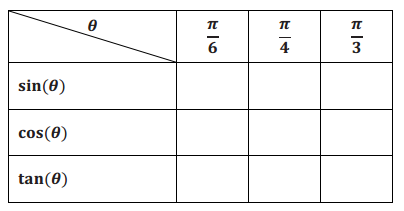
Answer:

Question 2.
Evaluate the following trigonometric expressions, and explain how you used the unit circle to determine your answer.
a. cos(π + \(\frac{\pi}{3}\))
Answer:
cos(π + \(\frac{\pi}{3}\)) = – cos(\(\frac{\pi}{3}\)) = – \(\frac{1}{2}\)
The rotation was \(\frac{\pi}{3}\) more than π bringing the ray to the third quadrant where cosine is negative.
cos(\(\frac{\pi}{3}\)) = \(\frac{1}{2}\) , so – cos(\(\frac{\pi}{3}\)) = – \(\frac{1}{2}\).

b. sin(π – \(\frac{\pi}{4}\))
Answer:
sin(π – \(\frac{\pi}{4}\)) = sin(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\)
The rotation was \(\frac{\pi}{4}\) less than π bringing the ray to the second quadrant where sine is positive.
sin(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\) , so sin(π – \(\frac{\pi}{4}\)) = sin⁡(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\).

c. sin(2π – \(\frac{\pi}{6}\))
Answer:
sin(2π – \(\frac{\pi}{6}\)) = – sin(\(\frac{\pi}{6}\)) = – \(\frac{1}{2}\)
The rotation was \(\frac{\pi}{6}\) less than 2π bringing the ray to the fourth quadrant where sine is negative.
sin(\(\frac{\pi}{6}\)) = \(\frac{1}{2}\) , so sin(2π – \(\frac{\pi}{6}\)) = – sin⁡(\(\frac{\pi}{6}\)) = – \(\frac{1}{2}\).

d. cos(π + \(\frac{\pi}{6}\))
Answer:
cos(π + \(\frac{\pi}{6}\)) = – cos(\(\frac{\pi}{6}\)) = – \(\frac{\sqrt{3}}{2}\)
The rotation was \(\frac{\pi}{6}\) more than π bringing the ray to the third quadrant where cosine is negative.
cos(\(\frac{\pi}{6}\)) = \(\frac{\sqrt{3}}{2}\) , so – cos(\(\frac{\pi}{6}\)) = – \(\frac{\sqrt{3}}{2}\).

e. cos(π – \(\frac{\pi}{4}\))
Answer:
cos(π – \(\frac{\pi}{4}\)) = – cos(\(\frac{\pi}{4}\)) = – \(\frac{\sqrt{2}}{2}\)
The rotation was \(\frac{\pi}{4}\) less than π bringing the ray to the second quadrant where cosine is negative.
cos(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\) , so – cos(\(\frac{\pi}{4}\)) = – \(\frac{\sqrt{2}}{2}\).

f. cos(2π – \(\frac{\pi}{3}\))
Answer:
cos(2π – \(\frac{\pi}{3}\)) = cos(\(\frac{\pi}{3}\)) = \(\frac{1}{2}\)
The rotation was \(\frac{\pi}{3}\) less than 2π bringing the ray to the fourth quadrant where cosine is positive.
cos(\(\frac{\pi}{3}\)) = \(\frac{1}{2}\) , so cos(\(\frac{5\pi}{3}\)) = \(\frac{1}{2}\).

g. tan(π + \(\frac{\pi}{4}\))
Answer:
tan(π + \(\frac{\pi}{4}\)) = tan(\(\frac{\pi}{4}\)) = 1
The rotation was \(\frac{\pi}{4}\) more than π bringing the ray to the third quadrant where tangent is positive.
tan(\(\frac{\pi}{4}\)) = 1 , so tan(\(\frac{5\pi}{4}\)) = 1.

h. tan(π – \(\frac{\pi}{6}\))
Answer:
tan(π – \(\frac{\pi}{6}\)) = – tan(\(\frac{\pi}{6}\)) = – \(\frac{1}{\sqrt{3}}\)
The rotation was \(\frac{\pi}{6}\) less than π bringing the ray to the second quadrant where tangent is negative.
tan(\(\frac{\pi}{6}\)) = \(\frac{1}{\sqrt{3}}\), so – tan(\(\frac{\pi}{6}\)) = – \(\frac{1}{\sqrt{3}}\).

i. tan(2π – \(\frac{\pi}{3}\))
Answer:
tan(2π – \(\frac{\pi}{3}\)) = – tan(\(\frac{\pi}{3}\)) = – \(\sqrt{3}\)
The rotation was \(\frac{\pi}{3}\) less than 2π bringing the ray to the fourth quadrant where tangent is negative. tan(\(\frac{\pi}{3}\)) = \(\sqrt{3}\), so – tan(\(\frac{\pi}{3}\)) = – \(\sqrt{3}\).

Question 2.
Rewrite the following trigonometric expressions in an equivalent form using π + θ, π – θ, or 2π – θ and evaluate.
a. cos(\(\frac{\pi}{3}\))
Answer:
cos(2π – \(\frac{\pi}{3}\)) = \(\frac{1}{2}\)

b. cos( – \(\frac{\pi}{4}\))
Answer:
cos(2π – \(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\)

c. sin(\(\frac{\pi}{6}\))
Answer:
sin(π – \(\frac{\pi}{6}\)) = \(\frac{1}{2}\)

d. sin(\(\frac{4\pi}{3}\))
Answer:
sin(π + \(\frac{\pi}{3}\)) = sin(2π – \(\frac{\pi}{3}\)) = – \(\frac{\sqrt{3}}{2}\)

e. tan( – \(\frac{\pi}{6}\))
Answer:
tan(π – \(\frac{\pi}{6}\)) = tan(2π – \(\frac{\pi}{6}\)) = – \(\frac{\sqrt{3}}{3}\)

f. tan( – 5\(\frac{\pi}{6}\))
Answer:
tan(π + \(\frac{\pi}{6}\)) = tan(2π + \(\frac{\pi}{6}\)) = \(\frac{\sqrt{3}}{3}\)

Question 4.
Identify the quadrant of the plane that contains the terminal ray of a rotation by θ if θ satisfies the given conditions.
a. sin(θ) > 0 and cos(θ) > 0
Answer:
Quadrant I

b. sin(θ) < 0 and cos(θ) < 0
Answer:
Quadrant III

c. sin(θ) < 0 and tan(θ) > 0
Answer:
Quadrant III

d. tan(θ) > 0 and sin(θ) > 0
Answer:
Quadrant I

e. tan(θ) < 0 and sin(θ) > 0
Answer:
Quadrant II

f. tan(θ) < 0 and cos(θ) > 0
Answer:
Quadrant IV

g. cos(θ) < 0 and tan(θ) > 0
Answer:
Quadrant III

f. sin(θ) > 0 and cos(θ) < 0
Answer:
Quadrant II

Question 5.
Explain why sin² (θ) + cos² (θ) = 1.
Answer:
For any real number θ the point (cos(θ),sin(θ)) lies on the unit circle with equation x² + y² = 1. Thus, we must have (cos(θ))² + (sin(θ))² = 1. With the shorthand notation (sin(θ))² = sin² (θ) and (cos(θ))² = cos² (θ), this gives sin² (θ) + cos² (θ) = 1.

Question 6.
Explain how it is possible to have sin(θ) < 0, cos(θ) < 0, and tan(θ) > 0. For which values of θ between 0 and 2π does this happen?
Answer:
Because tan(θ) = \(\frac{\sin (\theta)}{\cos (\theta)}\), if sin(θ) and cos(θ) are both negative, their quotient is positive. Thus, it is possible to have sin(θ) < 0, cos(θ) < 0, and tan(θ) > 0. This happens when the terminal ray of θ lies in the third quadrant, which is true for π < θ < \(\frac{3\pi}{2}\).

Question 7.
Duncan says that for any real number θ, tan⁡(θ) = tan⁡(π – θ). Is he correct? Explain how you know.
Answer:
No, Duncan is not correct. The terminal ray of rotation by θ and the terminal ray of rotation by π – θ are reflections of each other across the y – axis. Thus, (cos⁡(θ),sin⁡(θ)) is the reflection of (cos(π – θ),sin⁡(π – θ) ) across the
y – axis. This means that cos⁡(π – θ) = – cos⁡(θ) and sin⁡(π – θ) = sin⁡(θ).
Thus,
tan⁡(π – θ) = \(\frac{\sin (\pi – \theta)}{\cos (\pi – \theta)} = \frac{\sin (\theta)}{ – \cos (\theta)}\) = – tan⁡(θ).
We see that
tan⁡(π – θ) ≠ tan⁡(θ).

Question 8.
Given the following trigonometric functions, identify the quadrant in which the terminal ray of θ lies in the unit circle shown below. Find the other two trigonometric functions of θ of sin(θ), cos(θ), and tan(θ).

a. sin(θ) = \(\frac{1}{2}\) and cos(θ) > 0
Answer:
Quadrant I; θ = \(\frac{\pi}{6}\)
sin(θ) = \(\frac{1}{2}\) , cos(θ) = \(\frac{\sqrt{3}}{2}\), tan(θ) = \(\frac{\sqrt{3}}{3}\)

b. cos(θ) = – \(\frac{1}{2}\) and sin(θ) > 0
Answer:
Quadrant II; θ = \(\frac{\pi}{3}\)
sin(θ) = \(\frac{\sqrt{3}}{2}\), cos(θ) = – \(\frac{1}{2}\) , tan(θ) = – \(\sqrt{3}\)

c. tan(θ) = 1 and cos(θ) < 0
Answer:
Quadrant III; θ = \(\frac{\pi}{4}\)
sin(θ) = – \(\frac{\sqrt{2}}{2}\),cos(θ) = – \(\frac{\sqrt{2}}{2}\),tan(θ) = 1

d. sin(θ) = – \(\frac{\sqrt{3}}{2}\)and cot(θ) < 0
Answer:
Quadrant IV; θ = \(\frac{\pi}{3}\)
sin(θ) = – \(\frac{\sqrt{3}}{2}\), cos(θ) = \(\frac{1}{2}\) , tan(θ) = – \(\sqrt{3}\)

e. tan(θ) = – \(\sqrt{3}\) and cos(θ) < 0
Answer:
Quadrant II; θ = \(\frac{\pi}{3}\)
sin(θ) = \(\frac{\sqrt{3}}{2}\), cos(θ) = – \(\frac{1}{2}\) , tan(θ) = – \(\sqrt{3}\)

f. sec(θ) = – 2 and sin(θ) < 0 Answer: Quadrant III; θ = \(\frac{\pi}{3}\) sin(θ) = – \(\frac{\sqrt{3}}{2}\), cos(θ) = – \(\frac{1}{2}\) , tan(θ) = \(\sqrt{3}\) g. cot(θ) = \(\sqrt{3}\) and csc(θ) > 0
Answer:
Quadrant I; θ = \(\frac{\pi}{6}\)
sin(θ) = \(\frac{1}{2}\) , cos(θ) = \(\frac{\sqrt{3}}{2}\), tan(θ) = \(\frac{\sqrt{3}}{3}\)

Question 9.
Toby thinks the following trigonometric equations are true. Use θ = \(\frac{\pi}{6}\), \(\frac{\pi}{4}\), and \(\frac{\pi}{3}\) to develop a conjecture whether or not he is correct in each case below.
a. sin(θ) = cos(\(\frac{\pi}{2}\) – θ)
Answer:
sin(\(\frac{\pi}{6}\)) = \(\frac{1}{2}\) = cos(\(\frac{\pi}{3}\)) = cos(\(\frac{\pi}{2}\) – \(\frac{\pi}{6}\))
sin(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\) = cos(\(\frac{\pi}{4}\)) = cos(\(\frac{\pi}{2}\) – \(\frac{\pi}{4}\))
sin(\(\frac{\pi}{3}\)) = \(\frac{\sqrt{3}}{2}\) = cos(\(\frac{\pi}{6}\)) = cos(\(\frac{\pi}{2}\) – \(\frac{\pi}{3}\))
Yes, he seems to be correct.

b. cos(θ) = sin(\(\frac{\pi}{2}\) – θ)
Answer:
cos(\(\frac{\pi}{6}\)) = \(\frac{\sqrt{3}}{2}\) = sin(\(\frac{\pi}{3}\)) = sin(\(\frac{\pi}{2}\) – \(\frac{\pi}{6}\))
cos(\(\frac{\pi}{4}\)) = \(\frac{\sqrt{2}}{2}\) = sin(\(\frac{\pi}{4}\)) = sin(\(\frac{\pi}{2}\) – \(\frac{\pi}{4}\))
cos(\(\frac{\pi}{3}\)) = \(\frac{1}{2}\) = sin(\(\frac{\pi}{6}\)) = sin(\(\frac{\pi}{2}\) – \(\frac{\pi}{3}\))
Yes, he seems to be correct.

Question 10.
Toby also thinks the following trigonometric equations are true. Is he correct? Justify your answer.
a. sin(π – \(\frac{\pi}{3}\)) = sin(π) – sin(\(\frac{\pi}{3}\))
Answer:
He is not correct because trigonometric functions are not linear.
sin(π – \(\frac{\pi}{3}\)) = sin(\(\frac{\pi}{3}\)) = \(\frac{\sqrt{3}}{2}\)
sin(π) – sin(\(\frac{\pi}{3}\)) = 0 – \(\frac{\sqrt{3}}{2}\) = – \(\frac{\sqrt{3}}{2}\)

b. cos(π – \(\frac{\pi}{3}\)) = cos(π) – cos(\(\frac{\pi}{3}\))
Answer:
He is not correct because trigonometric functions are not linear.
cos(π – \(\frac{\pi}{3}\)) = cos(2\(\frac{\pi}{3}\)) = – \(\frac{1}{2}\)
cos(π) – cos(\(\frac{\pi}{3}\)) = – 1 – \(\frac{1}{2}\) = – \(\frac{3}{2}\)

c. tan(\(\frac{\pi}{3}\) – \(\frac{\pi}{6}\)) = tan(\(\frac{\pi}{3}\)) – tan(\(\frac{\pi}{6}\))
Answer:
He is not correct because trigonometric functions are not linear.
tan(\(\frac{\pi}{3}\) – \(\frac{\pi}{6}\)) = tan(\(\frac{\pi}{6}\)) = \(\frac{\sqrt{3}}{3}\)
tan(\(\frac{\pi}{3}\)) – tan(\(\frac{\pi}{6}\)) = \(\sqrt{3}\) – \(\frac{\sqrt{3}}{3}\) = \(\frac{2 \sqrt{3}}{3}\)

d. sin(π + \(\frac{\pi}{6}\)) = sin(π) + sin(\(\frac{\pi}{6}\))
Answer:
He is not correct because trigonometric functions are not linear.
sin(π + \(\frac{\pi}{6}\)) = – sin(\(\frac{\pi}{6}\)) = – \(\frac{1}{2}\)
sin(π) + sin(\(\frac{\pi}{6}\)) = 0 + \(\frac{1}{2}\) = \(\frac{1}{2}\)

e. cos(π + \(\frac{\pi}{4}\)) = cos(π) + cos(\(\frac{\pi}{4}\))
Answer:
He is not correct because trigonometric functions are not linear.
cos(π + \(\frac{\pi}{4}\)) = – cos(\(\frac{\pi}{4}\)) = – \(\frac{\sqrt{2}}{2}\)
cos(π) + cos(\(\frac{\pi}{4}\)) = – 1 + \(\frac{\sqrt{2}}{2}\) = \(\frac{ – 2 + \sqrt{2}}{2}\)

Eureka Math Precalculus Module 4 Lesson 1 Exit Ticket Answer Key

Question 1.
Evaluate the following trigonometric expressions, and explain how you used the unit circle to determine your answer.
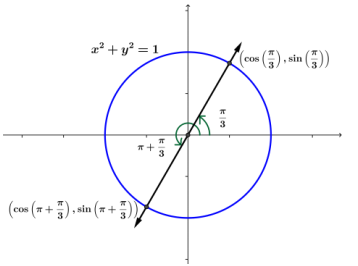
a. sin⁡(π + \(\frac{\pi}{3}\))
Answer:
sin⁡(π + \(\frac{\pi}{3}\)) = – sin(\(\frac{\pi}{3}\)) = – \(\frac{\sqrt{3}}{2}\)
Because the point (cos(π + \(\frac{\pi}{3}\)),sin(π + \(\frac{\pi}{3}\))) is directly opposite the point (cos(\(\frac{\pi}{3}\)),sin⁡(\(\frac{\pi}{3}\)) ), we know that the values of sin(\(\frac{\pi}{3}\)) and sin(π + \(\frac{\pi}{3}\)) are opposites.

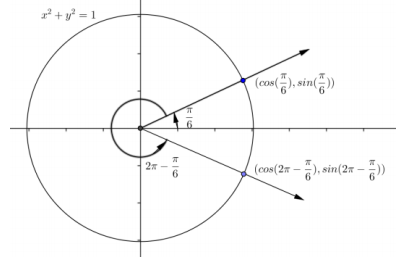
b. cos⁡(2π – \(\frac{\pi}{6}\))
Answer:
cos⁡(2π – \(\frac{\pi}{6}\)) = cos(\(\frac{\pi}{6}\)) = \(\frac{\sqrt{3}}{2}\)
Because the point (cos(2π – \(\frac{\pi}{6}\)),sin(2π – \(\frac{\pi}{6}\))) is the reflection of the point (cos(\(\frac{\pi}{6}\)),sin⁡(\(\frac{\pi}{6}\)) ) across the x – axis, we know that the values of cos(\(\frac{\pi}{6}\)) and cos(2π – \(\frac{\pi}{6}\)) are equal.

Question 2.
Corinne says that for any real number θ, cos⁡(θ) = cos⁡(θ – π). Is she correct? Explain how you know.
Answer:
Yes, Corinne is correct. The point (cos(θ),sin(θ)) reflects across the y – axis to (cos(π – θ),sin(π – θ)). These two points have opposite x – coordinates, so cos(π – θ) = cos(θ). Since the cosine function is an even function, cos⁡(π – θ) = cos⁡( – (θ – π)) = cos⁡(θ – π).
Thus, cos⁡(θ – π) = cos⁡(θ).