Eureka Math Precalculus Module 4 Lesson 10 Answer Key

Engage NY Eureka Math Precalculus Module 4 Lesson 10 Answer Key

Eureka Math Precalculus Module 4 Lesson 10 Example Answer Key

Example: Revisiting Vectors and Resultant Forces
The goalie on the soccer team kicks a ball with an initial force of 135 Newtons at a 40° angle with the ground. The mass of a soccer ball is 0.45 kg. Assume the acceleration due to gravity is 9.8\(\frac{\mathrm{m}}{\mathrm{s}^{2}}\) .
a. Draw a picture representing the force vectors acting on the ball and the resultant force vector.
Answer:
In the diagram below, F_b represents the force of the kick and F_g represents the force due to gravity.

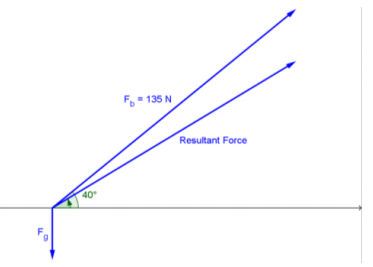
b. What is the magnitude of the resultant force vector?
Answer:
The force due to gravity is the product of the mass of the ball and the acceleration due to gravity.
F_g = 0.45∙9.8 = 4.41
Translating the gravitational force vector to the terminal point of the ball’s force vector and using the law of cosines gives the magnitude of the resultant force. The angle between the two vectors is 40° + 90° = 130°. This would make the angle in the triangle that we are using for law of cosines 50°. Let b represent the magnitude of the resultant force vector.
b² = 135² + 4.41² – 2(135)(4.41) cos⁡(50°)
b ≈ 132.21
The magnitude of the resultant force is approximately 132 newtons.

c. What are the horizontal and vertical components of this vector?
Answer:
The components of the initial force on the ball are 〈135 cos⁡(40°),135 sin⁡(40°)〉, and the components of the gravitational force vector are 〈0, – 4.41〉. Adding the vector components gives the resultant force in component form.
〈135 cos⁡(40°) + 0,135 sin⁡(40°) – 4.41〉 = 〈103.416,82.366〉

d. What is the angle of elevation of the resulting vector?
Answer:
Using right triangle trigonometry ratios, we can compute the angle of elevation.
tan⁡(θ) = \(\frac{82.366}{103.416}\)
θ = arctan⁡(\(\frac{82.366}{103.416}\))
θ ≈ 38.5°

Eureka Math Precalculus Module 4 Lesson 10 Exercise Answer Key

Opening Exercise
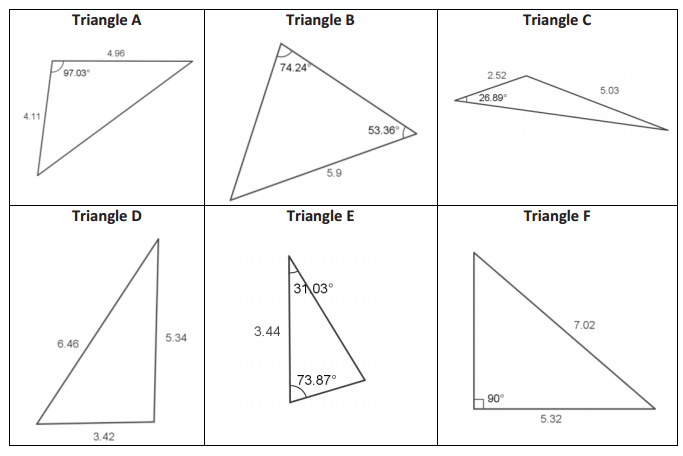
a. For each triangle shown below, decide whether you should use the law of sines, the law of cosines, or neither to begin finding the missing measurements. Explain how you know.

Answer:
Triangle A is solved using the law of cosines because we are given two sides and the included angle.
Triangle B is solved using the law of sines because we are given two angles and one side opposite one of the angles.
Triangle C is solved using the law of sines because we are given two sides and one angle with the angle being opposite one side.
Triangle D is solved using the law of cosines because three sides are given.
Triangle E is solved using the law of sines because two angles are given. We can easily find the third using the triangle sum theorem, and then we will have an angle and opposite side pairing.
Triangle F does not require the law of sines or the law of cosines because it is a right triangle. We can find the missing sides or angles using the Pythagorean theorem and right triangle trigonometry functions.

b. What types of given information will help you to decide which formula to use to determine missing measurements? Summarize your ideas in the table shown below:
Determining Missing Measurements

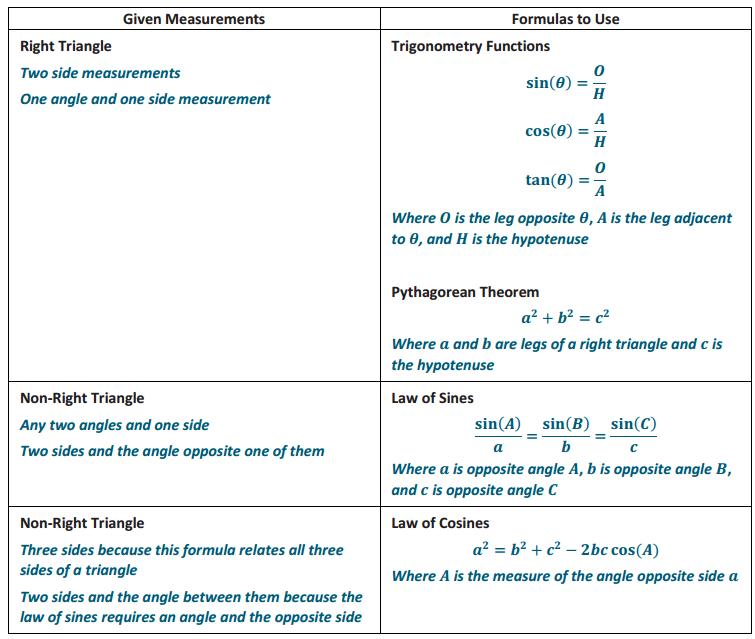
Answer:

Exercises 1–7
Exercise 1.
A landscape architect is given a survey of a parcel of land that is shaped like a parallelogram. On the scale drawing the sides of the parcel of land are 8 in. and 10 in., and the angle between these sides measures 75°. The architect is planning to build a fence along the longest diagonal. If the scale on the survey is 1 in.  = 120 ft., how long will the fence be?
Answer:

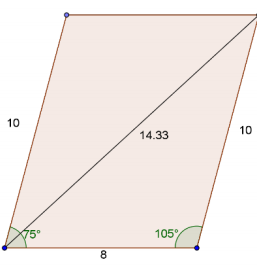
Let d be the measure of the longest diagonal.
d² = 10² + 8² – 2(10)(8) cos⁡(105°)
d ≈ 14.33
On the survey, this diagonal is approximately 14.33 in. The actual length of the fence will be 1,719.6 ft.

Exercise 2.
A regular pentagon is inscribed in a circle with a radius of 5 cm. What is the perimeter of the pentagon?
Answer:

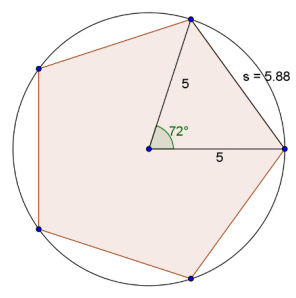
Let s be the measure of one side of the regular pentagon.
s² = 5² + 5² – 2(5)(5)cos⁡(72°)
s ≈ 5.88
Since there are five sides: 5∙5.88 = 29.4
Thus, the perimeter is 29.4 cm.

Exercise 3.
At the base of a pyramid, a surveyor determines that the angle of elevation to the top is 53°. At a point 75 meters from the base, the angle of elevation to the top is 35°. What is the distance from the base of the pyramid up the slanted face to the top?
Answer:

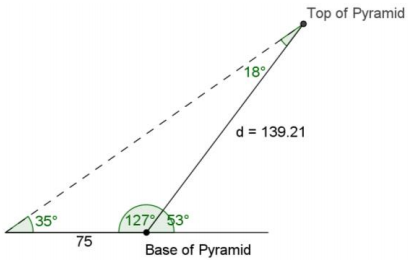
Let d be the distance from the base to the top of the pyramid.
\(\frac{\sin \left(18^{\circ}\right)}{75}\) = \(\frac{\sin \left(35^{\circ}\right)}{d}\)
d ≈ 139.21
The distance is approximately 139 meters.

Exercise 4.
A surveyor needs to determine the distance across a lake between an existing ferry dock at point A and a second dock across the lake at point B. He locates a point C along the shore from the dock at point A that is 750 meters away. He measures the angle at A between the sight lines to points B and C to be 65° and the angle at C between the sight lines to points A and B to be 82°. How far is it from the dock at A and the dock at B?
Answer:

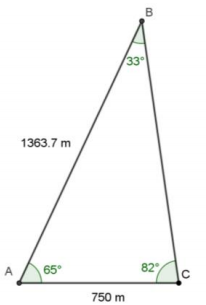
To find m∠B: 180° – (65° + 82°) = 33°.
Let d be the distance from the dock at A and the dock at B.
\(\frac{\sin \left(33^{\circ}\right)}{750}\) = \(\frac{\sin \left(82^{\circ}\right)}{d}\)
d ≈ 1363.7
The distance between the two docks across the lake is approximately 1,363.7 meters.

Exercise 5.
Two people located 500 yards apart have spotted a hot air balloon. The angle of elevation from one person to the balloon is 67°. From the second person to the balloon the angle of elevation is 46°. How high is the balloon when it is spotted?
Answer:

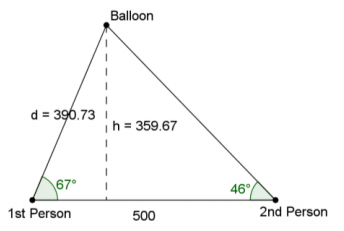
Let d be the distance between the first person and the balloon. Let h be the height of the balloon in the air.
By the law of sines,
\(\frac{\sin \left(46^{\circ}\right)}{d}\) = \(\frac{\sin \left(67^{\circ}\right)}{500}\)
d ≈ 390.73
Then,
sin⁡(67°) = \(\frac{h}{390.73}\)
h ≈ 359.67
The balloon is approximately 360 yards in the air when it is spotted.

When applying mathematics to navigation, direction is often given as a bearing. The bearing of an object is the degrees rotated clockwise from north that indicates the direction of travel or motion. The next exercises apply the law of cosines and the law of sines to navigation problems.
Exercise 6.
Two fishing boats start from a port. One travels 15 nautical miles per hour on a bearing of 25° and the other travels 18 nautical miles per hour on a bearing of 100°. Assuming each maintains its course and speed, how far apart will the fishing boats be after two hours?
Answer:

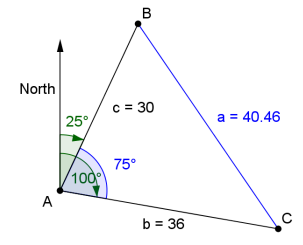
Let point A be the starting location of the two fishing boats at the port. After two hours one ship will have traveled 30 nautical miles from A to B. The other ship will have traveled 36 nautical miles from A to C. The law of cosines can be used to find the distance between the ships, a.
a² = 30² + 36² – 2(30)(36) cos⁡(75°)
a ≈ 40.46
The ships will be approximately 40.5 nautical miles apart after two hours.

Exercise 7.
An airplane travels on a bearing of 200° for 1500 miles and then changes to a bearing of 250° and travels an additional 500 miles. How far is the airplane from its starting point?
Answer:

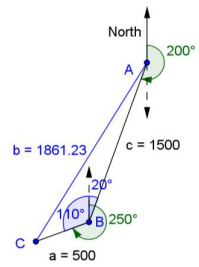
The measure of ∠ABC is 110° + 20°, or 130°. It is the sum of a 20° angle that is congruent to the angle formed by side c and the south – facing direction line from point A, and the difference between 250° and a full rotation of 360° about point B.
By the law of cosines, side b, which represents the distance from the starting point at A and the final point at C is given by
b² = 1500² + 500² – 2(1500)(500)cos⁡(130°)
b ≈ 1861.23
Thus, the airplane is approximately 1,861 miles from where it started. Note: This solution takes neither the elevation of the airplane nor the curvature of the Earth into account.

Exercises 8–10
Exercise 8.
Suppose a soccer player runs up to a moving soccer ball located at A and kicks the ball into the air. The diagram below shows the initial velocity of the ball along the ground and the initial velocity and direction of the kick. What is the resultant velocity and angle of elevation of the soccer ball immediately after it is kicked?

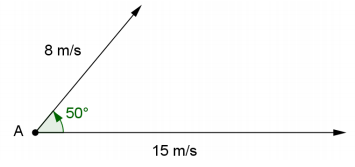
Answer:

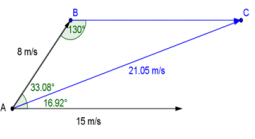
If we translate the vector with magnitude 15 m/s to point B, then the angle at B will be 130°. Then the sum of the two vectors is the vector with tail at the origin at C. Let b be the magnitude of this vector. By the law of cosines,
b = 8² + 15² – 2(8)(15) cos⁡(130°)
b ≈ 21.05
The direction can be found using the law of sines. Let θ be the angle between the 8 m/s vector and b.
\(\frac{\sin (\theta)}{15}\) = \(\frac{\sin \left(130^{\circ}\right)}{21.05}\)
θ = arcsin⁡(\(\frac{15 \sin \left(130^{\circ}\right)}{21.05}\))
θ ≈ 33.08°
Thus, the direction of the ball would be 50° – 33.08° = 16.92°.

Exercise 9.
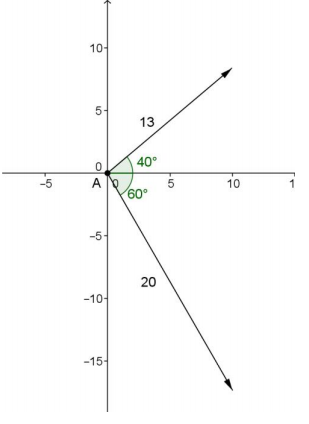
A 13 lb. force and a 20 lb. force are applied to an object located at A as shown in the diagram below. What is the resulting force and direction being applied to the object at A?

Answer:

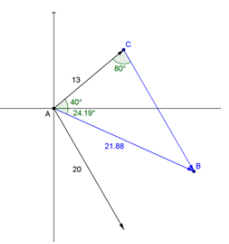
The resulting force is the sum of the two forces, which can be represented as vectors. The parallelogram rule gives us the resulting force vector. Using the law of cosines, we can determine the magnitude, and using the law of sines, we can determine the direction.
Let c be the distance between point A and B.
c² = 13² + 20² – 2(13)(20) cos⁡(80°)
c ≈ 21.88
The measure of ∠CAB can be found using the law of sines. Let θ be the measure of ∠CAB.
\(\frac{\sin \left(80^{\circ}\right)}{21.88}\) = \(\frac{\sin (\theta)}{20}\)
θ = arcsin⁡(\(\frac{20 \sin \left(80^{\circ}\right)}{21.88}\))
θ ≈ 64.19°
The resulting force of 21.88 lb. would be in a direction of 24.19° clockwise from the horizontal axis.

Exercise 10.
A motorboat travels across a lake at a speed of 10 mph at a bearing of 25°. The current of the lake due to the wind is a steady 2 mph at a bearing of 340°.
a. Draw a diagram that shows the two velocities that are affecting the boat’s motion across the lake.
Answer:

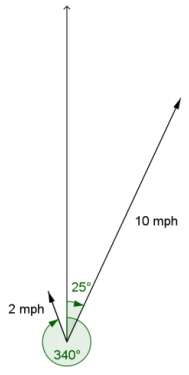
b. What is the resulting speed and direction of the boat?
Answer:

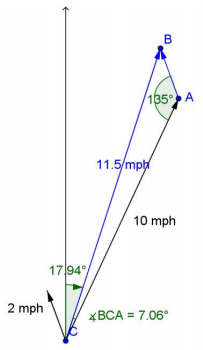
The resulting speed and direction is the sum of these two velocity vectors. Translating the current vector to the tip of the boat’s speed vector allows us to quickly draw the resulting vector. Its magnitude and direction can be determined using the law of cosines and the law of sines.
Let a be the distance between points C and B. By the law of cosines,
a² = 10² + 2² – 2(10)(2) cos⁡(135°)
a ≈ 11.5
Let θ be the measure of ∠BCA. Then, using the law of sines,
\(\frac{\sin \left(135^{\circ}\right)}{11.5}\) = \(\frac{\sin (\theta)}{2}\)
θ ≈ 7.06°
Then, bearing is 25° – 7.06° = 17.94°, and the speed is 11.5 mph.

Eureka Math Precalculus Module 4 Lesson 10 Problem Set Answer Key

Question 1.
For each of the situations below, determine whether to use the Pythagorean theorem, right triangle trigonometry, law of sines, law of cosines, or some other method.
a.

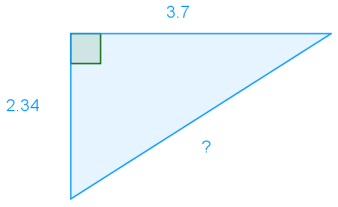
Answer:
Pythagorean theorem

b. Know one side and an angle of a right triangle and want to find any other side.
Answer:
Right triangle trigonometry

c.

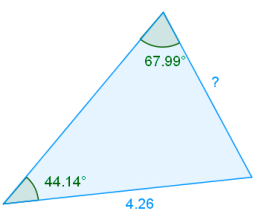
Answer:
Law of sines

d. Know two angles of a triangle and want to find the third.
Answer:
Find the sum of the measures of the two known angles, and subtract the result from 180°.

e.

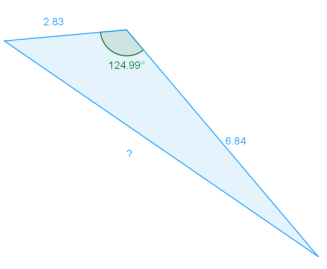
Answer:
Law of cosines

f. Know three sides of a triangle and want to find an angle.
Answer:
Law of cosines

g.

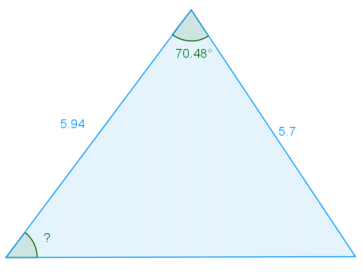
Answer:
Either law of cosines twice or a combination of law of cosines and law of sines

h. Know a side and two angles and want to find the third angle.
Answer:
Find the sum of the measures of the two known angles, and subtract the result from 180°.

i.

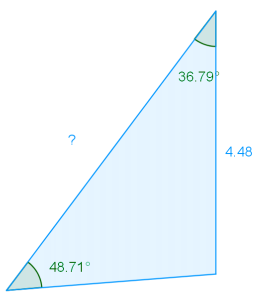
Answer:
Law of sines

Question 2.
Mrs. Lane’s trigonometry class has been asked to judge the annual unmanned hot – air balloon contest, which has a prize for highest flying balloon.
a. Sarah thinks that the class needs to set up two stations to sight each balloon as it passes between them. Construct a formula that Mrs. Lane’s class can use to find the height of the balloon by plugging the two angles of elevation so that they can program their calculators to automatically output the height of the balloon. Use 500 ft. for the distance between the stations and α and β for the angles of elevation.
Answer:
b = 500 \(\frac{\sin (\beta)}{\sin \left(180^{\circ} – \alpha – \beta\right)}\)
h = b sin⁡(α)
h = \(\frac{500 \sin (\alpha) \sin (\beta)}{\sin \left(180^{\circ} – \alpha – \beta\right)}\)

b. The students expect the balloons to travel no higher than 500 ft. What distance between the stations would you recommend? Explain.
Answer:
Answers may vary. Depending on how close the balloons pass to the stations, students may be sighting the balloon at near vertical angles. More accurate measurements can probably be obtained the closer the balloons are to 45° from the stations, so a distance of greater than 500 ft. is probably better suited.

c.
Find the heights of balloons sighted with the following angles of elevation to the nearest ten feet. Assume a distance of 500 ft. between stations.
i. 5°, 15°
Answer:
32.977 ft. ≈ 30 ft.

ii. 38°, 72°
Answer:
311.553 ft. ≈ 310 ft.

iii. 45°, 45°
Answer:
250 ft.

iv. 45°, 59°
Answer:
312.33 ft. ≈ 310 ft.

v. 28°, 44°
Answer:
171.45 ft. ≈ 170 ft.

vi. 50°, 66°
Answer:
389 ft. ≈ 390 ft.

vii. 17°, 40°
Answer:
112 ft. ≈ 110 ft.

d. Based on your results in part (c), which balloon won the contest?
Answer:
The student with the balloon that went 390 ft.

e. The balloons were released several hundred feet away but directly in the middle of the two stations. If the first angle represents the West station and the second angle represents the East station, what can you say about the weather conditions during the contest?
Answer:
It appears as though a wind was blowing the balloons to the east.

f. Are there any improvements to Mrs. Lane’s class’s methods that you would suggest? Explain.
Answer:
Answers may vary. Students could suggest higher degrees of accuracy by adjusting the distance between the students. Multiple angles of elevation could be taken from different spots, or additional students could help measure to minimize human error.

Question 3.
Bearings on ships are often given as a clockwise angle from the direction the ship is heading (0° represents something in the path of the boat, and 180° represents something behind the boat). Two ships leave port at the same time. The first ship travels at a constant speed of 30 kn. After 2 \(\frac{1}{2}\) hours, the ship sights the second at a bearing of 110° and 58 nautical miles away.
a. How far is the second ship from the port where it started?
Answer:
109 nautical miles from port

b. How fast is the second ship traveling on average?
Answer:
\(\frac{109}{2.5}\) = 43.6; The second ship is traveling 43.6 kn.

Question 4.
A paintball is fired from a gun with a force of 59 N at an angle of elevation of 1°. If the force due to gravity on the paintball is 0.0294 N, then answer the following:
a. Is this angle of elevation enough to overcome the initial force due to gravity and still have an angle of elevation greater than 0.5°?
Answer:
Yes. The force due to gravity is so small that there is effectively no difference initially. The third side has a magnitude of 58.999. The angle of elevation is reduced by less than 0.029°.

b. What is the resultant magnitude of the vector in the direction of the paintball?
Answer:
58.999 N

Question 5.
Valerie lives 2 miles west of her school and her friend Yuri lives 3 miles directly northeast of her.
a. Draw a diagram representing this situation.
Answer:

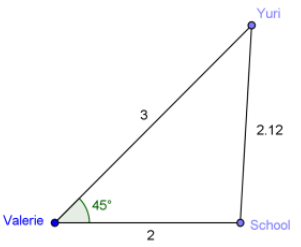
b. How far does Yuri live from school?
Answer:
c = \(\sqrt{2^{2} + 3^{2} – 2 \cdot 2 \cdot 3 \cdot \cos (45)}\)
= \(\sqrt{13 – 6 \sqrt{2}}\)
≈ 2.125
Yuri lives approximately 2.125 mi. from school.

c. What is the bearing of the school to Yuri’s house?
Answer:
arccos⁡(\(\frac{9 – 2.125^{2} – 4}{ – 8.499}\)) ≈ 93.27
Yuri’s house is 93.27° N of W from the school, so the school is on a bearing of – 176.73 from N. This can be worded different ways, for instance, 86.73° S of W, 93.27° S of E.

Question 6.
A 2.1 kg rocket is launched at an angle of 33° with an initial force of 50 N. Assume the acceleration due to gravity is 9.81 m/s² .
a. Draw a picture representing the force vectors and their resultant vector.
Answer:

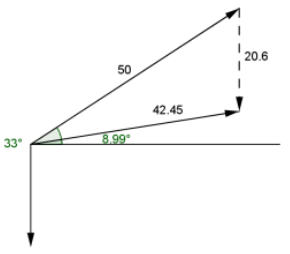
b. What is the magnitude of the resultant vector?
Answer:
The force due to gravity: F = 2.1⋅9.81 = 20.601
c = \(\sqrt{50^{2} + 20.601^{2} – 2 \cdot 50 \cdot 20.601 \cdot \cos \left(57^{\circ}\right)}\)
≈ 42.455
The resultant vector is about 42.455 N.

c. What are the horizontal and vertical components of the resultant vector?
Answer:
The initial force of the rocket can be expressed by the vector 〈50 cos⁡(33°),50 sin⁡(33°)〉. The force due to gravity can be expressed by 〈0,20.601〉. The resultant vector is 〈41.934,6.631〉.

d. What is the angle of elevation of the resultant vector?
Answer:
arctan⁡(\(\frac{6.631}{41.934}\)) ≈ 8.986
The angle of elevation is about 8.986°.

Question 7.
Use the distance formula to find c, the distance between A and B for △ABC, with A = (b cos⁡(γ),b sin⁡(γ) ), B = (a,0), and C = (0,0). After simplifying, what formula have you proven?
Answer:
AB = \(\sqrt{(b \cos (\gamma) – a)^{2} + (b \sin (\gamma))^{2}}\)
Multiplying out on the inside of the square root, we get
b² (cos⁡(γ))² – 2ab cos⁡(γ) + a² + b² (sin⁡(γ))².
Factoring out b², we get
b² ((cos⁡(γ) )² + (sin⁡(γ) )² ) – 2ab cos⁡(γ) + a² = b² + a² – 2abcos(γ).
So we have
AB = \(\sqrt{a^{2} + b^{2} – 2 a b \cos (\gamma)}\).
Since △ABC could be any triangle translated to the origin and rotated so that one side lays on the x – axis, we have proven the law of cosines.

Question 8.
For isosceles triangles with a = b, show the law of cosines can be written as cos⁡(γ) = 1 – \(\frac{c^{2}}{2 a^{2}}\).
Answer:
c² = a² + b² – 2ab cos⁡(γ)
c² = 2a² – 2a² cos⁡(γ)
c² = 2a² (1 – cos⁡(γ) )
\(\frac{c^{2}}{2 a^{2}}\) = 1 – cos⁡(γ)
cos⁡(γ) = 1 – \(\frac{c^{2}}{2 a^{2}}\)

Eureka Math Precalculus Module 4 Lesson 10 Exit Ticket Answer Key

Question 1.
A triangular pasture is enclosed by fencing measuring 25, 35, and 45 yards at the corner of a farmer’s property.

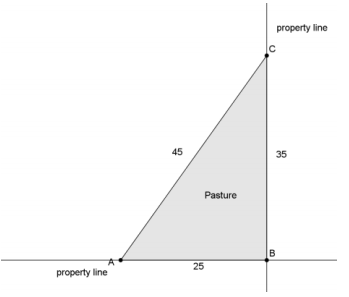
a. According to the fencing specifications, what is the measure of ∠ABC?
Answer:
45² = 25² + 35² – 2⋅25⋅35⋅cos⁡(B)
B = arccos⁡(\(\frac{45^{2} – 25^{2} – 35^{2}}{ – 2 \cdot 25 \cdot 35}\))
= arccos⁡( – 0.1)
≈ 95.739
The measure of ∠ABC is 95.739°.

b. A survey of the land indicates that the property lines form a right angle at B. Explain why a portion of the pasture is actually on the neighboring property.
Answer:
If the fencing went along the actual property lines, then the angle at B would be 90°. Since it is larger than 90°, a portion of the pasture must lie in the adjacent property.

c. Where does the 45 – yard section of the fence cross the vertical property line?
Answer:

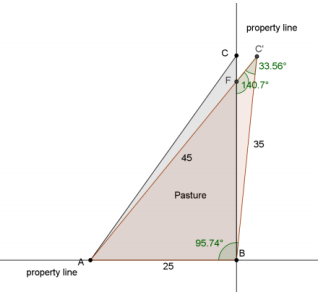
C’ = arcsin⁡(25⋅\(\frac{\sin \left(95.74^{\circ}\right)}{45}\)) ≈ 33.56°
The measure of ∠FBC’ is 5.74°, and the measure of ∠C’FB is 140.7°. Let c’ be the measure of segment BF.
\(\frac{\sin \left(33.56^{\circ}\right)}{c^{\prime}}\) = \(\frac{\sin \left(140.7^{\circ}\right)}{35}\)
c’ ≈ 30.55
The 45 – yard section of fence crosses the vertical property line approximately 30.55 yards from point B.