Eureka Math Precalculus Module 4 Mid Module Assessment Answer Key

Engage NY Eureka Math Precalculus Module 4 Mid Module Assessment Answer Key

Eureka Math Precalculus Module 4 Mid Module Assessment Task Answer Key

Question 1.
An equilateral triangle is drawn within the unit circle centered at the origin as shown.

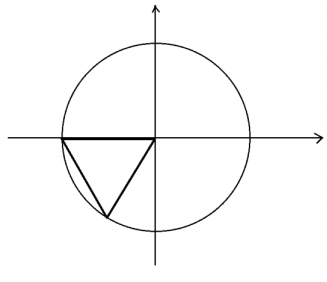
Explain how one can use this diagram to determine the values of sin(\(\frac{4\pi}{2}\)),cos⁡(\(\frac{4\pi}{2}\)), and tan⁡(\(\frac{4\pi}{2}\)).
Answer:
Interior angle of an equilateral triangle has a measure of \(\frac{\pi}{3}\) and so the measure of the angle x shown is π + \(\frac{\pi}{3}\) = \(\frac{4\pi}{3}\).

Draw the altitude of the equilateral triangle, and mark the indicated lengths a and b as shown. We have that cos ⁡(x ) = -a and sin ⁡(x ) = -b .

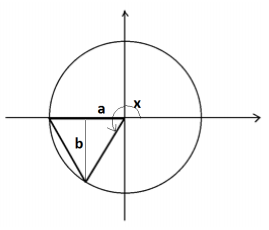
Now a is half the base of an equilateral triangle of side length 1 , so a = 1 /2 . By the Pythagorean theorem,
b = \(\sqrt{(1)^{2}-\left(\frac{1}{2}\right)^{2}}\) = \(\sqrt{\frac{3}{4}}\) = \(\frac{\sqrt{3}}{2} \mid\). Thus, we have the following:
cos ⁡(\(\frac{4\pi}{3}\) ) = – \(\frac{1}{2}\)
sin ⁡(\(\frac{4\pi}{3}\) ) = – \(\frac{\sqrt{3}}{2} \mid\)
tan ⁡(\(\frac{4\pi}{3}\) ) = \(\frac{\sin \left(\frac{4 \pi}{3}\right)}{\cos \left(\frac{4 \pi}{3}\right)}\) = \(\frac{-\frac{\sqrt{3}}{2}}{-\frac{1}{2}}\) = \(\sqrt{3}\)

Question 2.
Suppose x is a real number with 0 < x < \(\frac{\pi}{4}\).

a. Set a=sin(π-x), b=cos(π+x), c=sin(x-π), and d=cos(2π-x).
Arrange the values a, b, c, and d in increasing order, and explain how you determined their order.
Answer:
Draw the unit circle and the point P on the circle with coordinates ( cos ⁡(x ), sin ⁡(x)) . Because 0 < x < \(\frac{\pi}{4}\) , we have that both sin ⁡(x) and cos ⁡(x) are positive numbers with
sin ⁡(x ) < cos ⁡(x) .

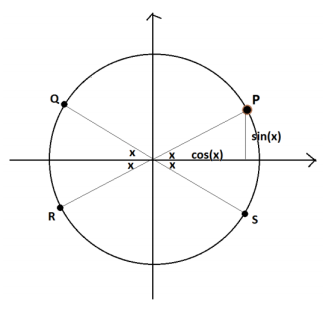
The points Q,R , and S on the diagram have coordinates:
Q = ( cos ⁡(π – x ),(π – x))
R = ( cos ⁡(π + x),sin(π + x))
S = ( cos ⁡(2π – x ), sin ⁡(2π – x))
We also see from the diagram that ( cos ⁡(x – π ), sin ⁡(x – π)) is also the point R .
From the diagram we have
a = sin ⁡(π – x ) = sin ⁡(x) (looking at the point Q ),
b = cos ⁡(π + x ) = -cos ⁡(x) (looking at the point R ),
c = sin ⁡(x – π ) = -sin ⁡(x) (looking at the point R ),
d = cos ⁡(2π – x ) = cos ⁡(x) (looking at the point S ).
Since sin ⁡(x ) < cos ⁡(x) it follows that b < c < a < d .

b. Use the unit circle to explain why tan⁡(π-x)=-tan⁡(x).
Answer:
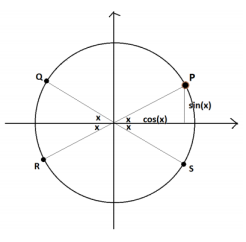
Look at the diagram of the four points on the unit circle from the previous question.
We are interested in tan ⁡(π-x )= sin ⁡(π – x )/cos ⁡(π – x ) The point Q has coordinates (cos ⁡(π – x ), sin ⁡(π – x)) and we see, in relation to the point P , that sin ⁡(π – x ) = sin ⁡(x) and cos ⁡(π – x ) = – cos ⁡(x) . Thus,
tan ⁡(π – x ) = \(\frac{\sin (\pi-x)}{\cos (\pi-x)}\) = \(\frac{\sin (x)}{-\cos (x)}\) = – \(\frac{\sin (x)}{\cos (x)}\) = – tan ⁡(x) .

Question 3.
a. Using a diagram of the unit circle centered at the origin, explain why f(x)⁡=cos⁡(x) is an even function.
Answer:
We need to show that f(-x) = f(x) , that is, cos(-x) = cos(x) for all real numbers x .
Let d represent the length of the segment shown in the diagram. We see symmetry in the diagram.
From the diagram, cos(x) = -d and cos(-x) = -d , that is, cos(x) = cos(-x) .

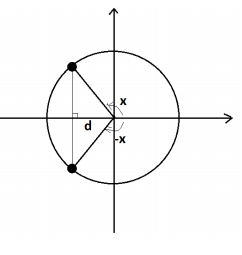
Note: Here we drew a diagram with x representing the measure of an obtuse angle. The same symmetry applies to all types of angles.

b. Using a diagram of the unit circle centered at the origin, explain why sin⁡(x-2π)=sin⁡(x) for all real values x.
Answer:
We see from a diagram that the points on the unit circle with coordinates (cos ⁡(x ), sin ⁡(x)) and (cos ⁡(x – 2π ), sin ⁡(x – 2π)) coincide.

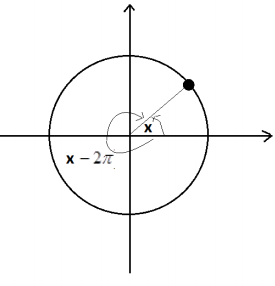
Thus, sin ⁡(x – 2π ) = sin ⁡(x) .

c. Explain why tan⁡(x+π)=tan⁡(x)for all real values x.
Answer:
The symmetry of the following diagram shows that sin ⁡(x + π ) = – sin ⁡(x) and
cos ⁡(x + π ) = – cos ⁡(x) .

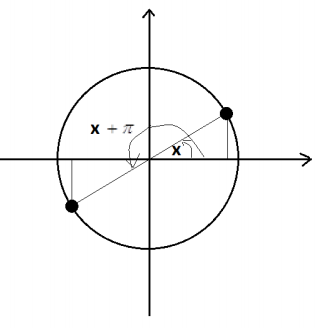
Thus,
tan ⁡(x + π )= \(\frac{\sin (x+\pi)}{\cos (x+\pi)}\) = \(\frac{-\sin (x)}{-\cos (x)}\) = \(\frac{\sin (x)}{\cos (x)}\) = tan ⁡(x ).

Question 4.
The point P shown lies outside the circle with center O. Point M is the midpoint of \(\overline{O P}\).

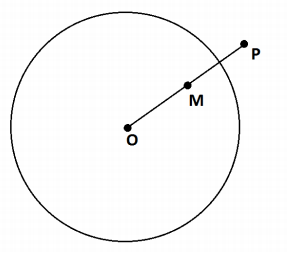
a. Use a ruler and compass to construct a line through P that is tangent to the circle.
Answer:
Draw a circle with center M and with radius set to the length OM . This new circle intersects the original circle at two points. Call one of those two points Q .

Draw the line through P and Q . This is a line through P and tangent to the circle.

b. Explain how you know that your construction does indeed produce a tangent line.
Answer:
Reason: Since we drew a circle with center M , we have MO = MQ = MP . Call this common length r . Thus, we have a diagram containing two isosceles triangles.

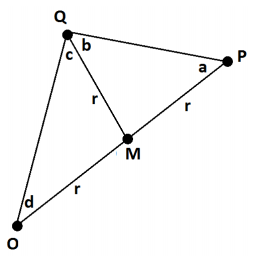
Mark the angles a , b , c , and d as shown.
Because they are base angles of an isosceles triangle, a = b .
Because they are base angles of an isosceles triangle, d = c .
Because angles in a triangle sum to π radians,
a + b + c + d = π .
That is, 2b + 2c = π giving
b + c = \(\frac{\pi}{2}\) .
Thus, the radius \(\overline{O Q}\) in the original circle meets \(\overleftrightarrow{P Q}\) at a right angle. It must be then that \(\overleftrightarrow{P Q}\) is indeed a tangent line to the original circle.

Question 5.
Each rectangular diagram below contains two pairs of right triangles, each having a hypotenuse of length 1. One pair of triangles has an acute angle measuring x radians. The other pair of triangles has an acute angle measuring y radians.

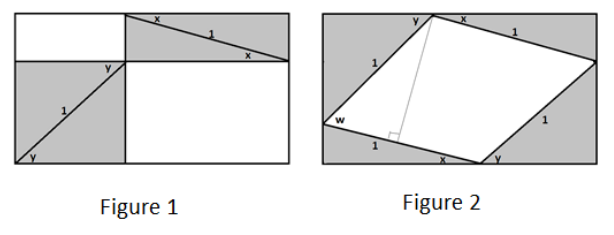
a. Using Figure 1, write an expression, in terms of x and y, for the area of the non-shaded region.
Answer:
The right triangles used in the diagrams have side lengths as shown:

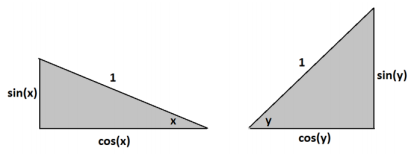
In Figure 1, the area we seek is the sum of areas of two rectangles: one sin ⁡(x) -by-cos ⁡(y) rectangle and one sin (y) – by – cos ⁡(x) rectangle.

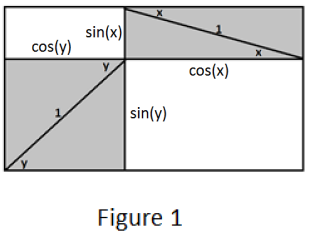
Thus, the area under consideration is given by sin ⁡(x) cos ⁡(y) + sin ⁡(y) cos ⁡(x) .

b. Figure 2 contains a quadrilateral which is not shaded and contains angle w. Write an expression, in terms of x and y, for the measure of angle w.
Answer:
In Figure 2, we see that three angles of measures \(\frac{\pi}{2}\) – x , w , and \(\frac{\pi}{2}\) – y form a straight angle:

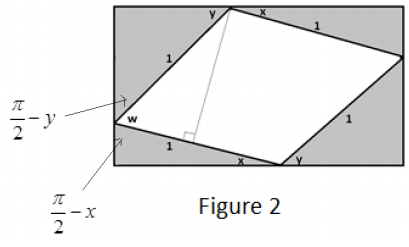
Thus, w = π – (\(\frac{\pi}{2}\) – x )- (\(\frac{\pi}{2}\) – y ) = x + y .

c. Using Figure 2, write an expression, in terms of w, for the non-shaded area. Explain your work.
Answer:
We seek the area of a rhombus with a side length of 1 . The area of a rhombus (or any parallelogram) is given by “base times height.” Here the base is 1 .
Now w is an angle in a right triangle with hypotenuse 1 . Noting this, we see that the height of our rhombus is sin ⁡(w) . Thus, the area we seek is 1 × sin ⁡(w ) = sin ⁡(w) .

d. Use the results of parts (a), (b), and (c) to show why sin⁡(x+y)=sin⁡(x) cos⁡(y)+sin⁡(y) cos⁡(x) is a valid formula.
Answer:
The area inside the rectangle but outside the four right triangles is the same for both diagrams. Thus, our two different computations for this common area must be the same:
sin ⁡(x ) cos ⁡(y ) + cos ⁡(x ) sin ⁡(y ) = sin ⁡(w) .

Since w = x + y , we have the following formula:
sin ⁡(x + y ) = sin ⁡(x ) cos ⁡(y ) + cos ⁡(x ) sin ⁡(y) .

e. Suppose α is a real number between \(\frac{\pi}{2}\) and π and y is a real number between 0 and \(\frac{\pi}{2}\). Use your result from part (d) to show the following:
cos⁡(α+y)=cos⁡(α) cos⁡(y)-sin⁡(α) sin⁡(y).
Explain your work.
Answer:
The formula we derived in part (d) is valid for any two real numbers x and y that represent the measures of acute angles. If \(\frac{\pi}{2}\) < α < π , then 0 < α – \(\frac{\pi}{2}\) < \(\frac{\pi}{2}\). Let’s set
x = α – \(\frac{\pi}{2}\) . Then x and y are two real numbers representing the measures of acute angles, and so we have the following:
sin ⁡(x + y ) = sin ⁡(x ) cos ⁡(y ) + cos ⁡(x ) sin ⁡(y) .

This reads
sin ⁡(α + y – \(\frac{\pi}{2}\)) = sin ⁡(α – \(\frac{\pi}{2}\)) cos ⁡(y ) + cos ⁡(α – \(\frac{\pi}{2}\)) sin ⁡(y) .

Using sin ⁡(θ – \(\frac{\pi}{2}\)) = – cos ⁡(θ) and cos ⁡(θ – \(\frac{\pi}{2}\)) = sin ⁡(θ) , we see the following:
– cos ⁡(α + y ) = – cos ⁡(α ) cos ⁡(y ) + sin ⁡(α ) sin ⁡(y) .

Multiplying through by -1 gives the result stated in the question.

Question 6.
A rectangle is drawn in a semicircle of radius 3 with its base along the base of the semicircle as shown.

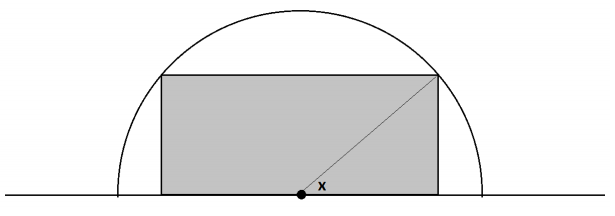
Find, to two decimal places, values for real numbers a and b so that a cos⁡(x+b) represents the perimeter of the rectangle if the real number x is the measure of the angle shown.
Answer:
We see that the perimeter of the rectangle is
2 ∙ 3 sin ⁡(x ) + 4 ∙ 3 cos ⁡(x ) = 6 sin ⁡(x ) + 12 cos ⁡(x) .

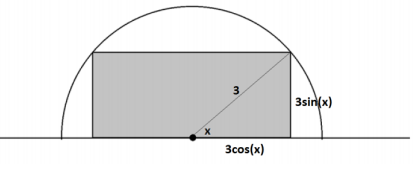
We wish to write this expression in the form a cos ⁡(x + b) :
a cos ⁡(x + b ) = a cos ⁡(x ) cos ⁡(b )- a sin ⁡(x ) sin ⁡(b) .
This suggests the following:
a cos ⁡(b ) = 12
-a sin ⁡(b ) = 6
Using sin ² (b ) + cos ² (b ) = 1 this gives \(\frac{144}{a^{2}}+\frac{36}{a^{2}}\) = 1
Therefore, a = \(\sqrt{180}\) ≈ 13.42 is a candidate value for a .
Also,
-tan ⁡(b )=\(\frac{-a \sin (b)}{a \cos (b)}\)
-tan ⁡(b )=\(\frac{6}{12}\)
b=tan^-1 (-\(\frac{1}{2}\))
b≈-0.46
Thus b , is the measure of an angle in the fourth quadrant in this instance.
So let’s examine 13.42 cos ⁡(x – 0.46) :
13.42 cos ⁡(x -0.46 )=13.42 cos ⁡(x ) cos ⁡(-0.46 )-13.42 sin ⁡(x ) sin ⁡(-0.46 )
≈ 13.42⋅cos ⁡(x )⋅0.90 – 13.42 ⋅sin ⁡(x) ⋅(-0.44)
≈ 12 cos ⁡(x ) + 6 sin ⁡(x)
Therefore, the two numbers that gives us an expression, a cos(x – b), that represents the perimeter of the rectangle are a = 13.42 and b = -0.46 .