Engage NY Eureka Math Precalculus Module 5 Lesson 15 Answer Key
Eureka Math Precalculus Module 5 Lesson 15 Exercise Answer Key
Exercises 1–2
Exercise 1.
The club advisors only want to offer one product this year. They have decided to let the club members choose which product to offer and have shared the records from past years. Assuming that these probability distributions were to hold for the coming fundraiser, which product should the club members recommend they sell? Explain.
Answer:
The expected revenues for the three products are as follows:
Candy
($100)(0.10) + ($200)(0.10) + ($300)(0.25) + ($400)(0.45) + ($500)(0.05) + ($600)(0.05) = $340.00
(Be sure students include the units and dollars, and not just the raw number 340.)
Magazine subscriptions
($200)(0.4) + ($300)(0.4) + ($400)(0.2) = $280.00
Wrapping paper
($300)(1) = $300.00
Because the expected revenue is the highest for candy, it is recommended that the math club sell this product.
Exercise 2.
The club advisors forgot to include overhead costs with the past revenue data.
The overhead costs are $80.00 for candy, $20.00 for magazine subscriptions, and $40.00 for wrapping paper. Will this additional information change the product that the math club members recommend they sell? Why?
Answer:
The math club’s decision should not be based solely on expected revenue. Expenses have been incurred in producing the product. Such expenses are referred to as overhead costs. The result of revenue minus overhead cost yields profit. Based on expected profit, the math club can randomly choose one of the products since they all yield the same expected profit.
The expected profit for producing candy is $340.00-$80.00 = $260.00.
The expected profit for producing magazine subscriptions is
$280.00-$20.00 = $260.00.
The expected profit for producing wrapping paper is $300.00-$40.00 = $260.00.
Exercises 3–4
Exercise3.
Suppose that you want to buy a $7,500.00 pre-owned car. What should you do? Take the $5,000.00, or choose a box? Why?
Answer:
Answers will vary. Some students may say to take the $5,000.00 since it is guarenteed money rather than potential money. But what if there is no way to earn the remaining $2,500.00? Hopefully, a student will argue that a decision should be made based on the expected winning by playing the game. By choosing a box at random, the expected winning is ($1)(\(\frac{1}{4}\)) + ($15)(\(\frac{1}{4}\)) + ($15000)(\(\frac{1}{4}\)) + ($40000)(\(\frac{1}{4}\)) = $13754.00. That would be enough to buy the car, plus insurance and gas for an extended period of time.
Exercise 4.
What should you do if you want to buy a $20,000.00 brand-new car? Take the $5,000.00, or choose a box? Why?
Answer:
Just as in Exercise 3, there really isn’t a right or wrong answer to the question posed in Exercise 4. But it will be interesting to hear students’ arguments on both sides.
Exercises 5–14
Exercise 5.
What are the possible values for the total points Henry can earn in a match? For example, he can earn 1 \(\frac{1}{2}\) points by WT or TW (he wins the first game and ties the second game or ties the first game and wins the second game). What are the other possible values?
Answer:
The possible numbers of points earned in a match are the entries in the following matrix. The possibilities are 0, \(\frac{1}{2}\), 1, 1 \(\frac{1}{2}\), 2 as shown in the following table.
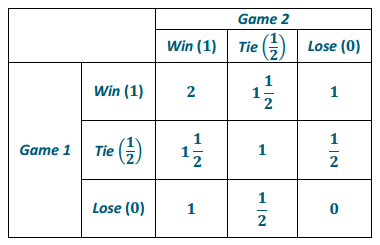
Exercise 6.
If Henry plays both games boldly (BB), find the probability that Henry will earn
a. 2 points
Answer:
0.2025
b. 1 \(\frac{1}{2}\) points
Answer:
0.0
c. 1 point
Answer:
0.495
d. \(\frac{1}{2}\) points
Answer:
0.0
e. 0 points
Answer:
0.3025
If Henry plays both games boldly, the following table gives the possible points earned and the probabilities (printed below the points).
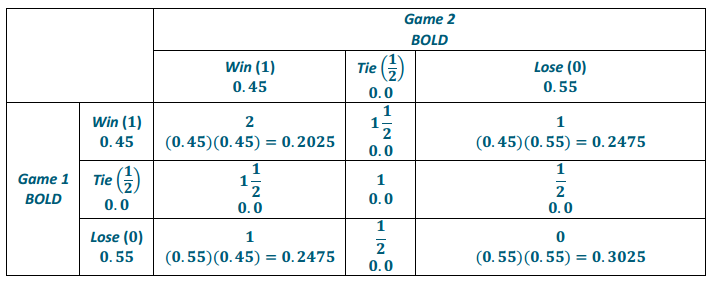
Exercise 7.
What is the expected number of points that Henry will earn if he plays using a BB strategy?
Answer:
(2)(0.2025) + (1)(0.2475) + (1)(0.2475) + (0)(0.3025) = 0.9
Henry’s expected number of points won using the BB strategy is 0.9 points. (Be sure students include the units.)
Exercise 8.
If Henry plays both games conservatively (CC), find the probability that Henry will earn
a. 2 points
Answer:
0.0
b. 1 \(\frac{1}{2}\) points
Answer:
0.0
c. 1 point
Answer:
0.64
d. \(\frac{1}{2}\) points
Answer:
0.32
e. 0 points
Answer:
0.04
If Henry plays both games conservatively, the following table gives the possible points earned and the probabilities (printed below the points).
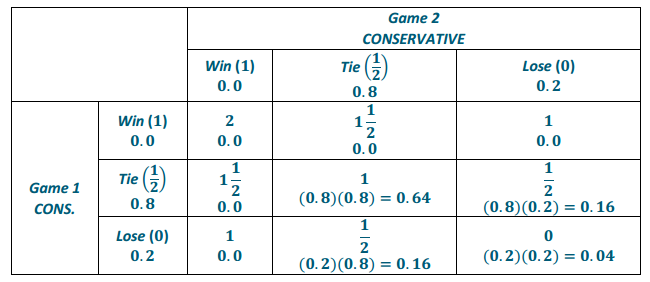
Exercise 9.
What is the expected number of points that Henry will earn if he plays using a CC strategy?
Answer:
(1)(0.64) + (\(\frac{1}{2}\))(0.16) + (\(\frac{1}{2}\))(0.16) + (0)(0.04) = 0.8
Henry’s expected number of points won using the CC strategy is 0.8 points.
Exercise 10.
If Henry plays the first game boldly and the second game conservatively (BC), find the probability that Henry will earn
a. 2 points
Answer:
0.0
b. 1 \(\frac{1}{2}\) points
Answer:
0.36
c. 1 point
Answer:
0.09
d. \(\frac{1}{2}\) points
Answer:
0.44
e. 0 points
Answer:
0.11
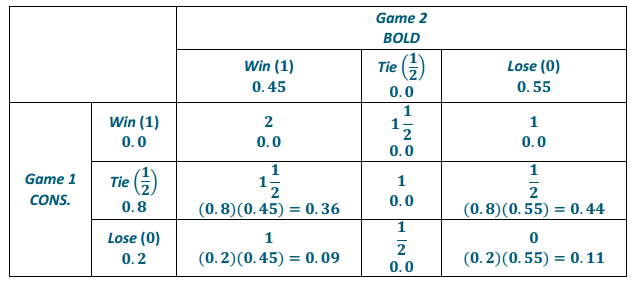
If Henry plays the first game boldly and the second game conservatively, the following table gives the possible points earned and the probabilities (printed below the points).
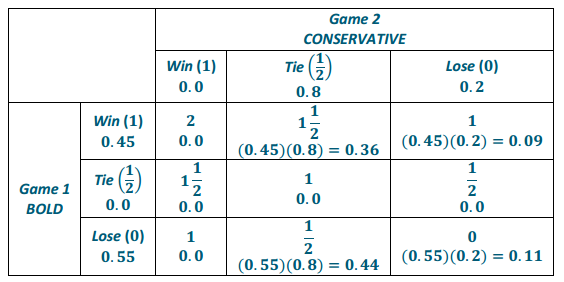
Exercise 11.
What is the expected number of points that Henry will earn if he plays using a BC strategy?
Answer:
(1 \(\frac{1}{2}\))(0.36) + (1)(0.09) + (\(\frac{1}{2}\))(0.44) + (0)(0.11) = 0.85
Henry’s expected number of points won using the BC strategy is 0.85 points.
Exercise 12.
If Henry plays the first game conservatively and the second game boldly (CB), find the probability that Henry will earn
a. 2 points
Answer:
0.0
b. 1 \(\frac{1}{2}\) points
Answer:
0.36
c. 1 point
Answer:
0.09
d. \(\frac{1}{2}\) points
Answer:
0.44
e. 0 points
Answer:
0.11
Note: Some students may see the symmetry between BC and CB and conclude without calculation that CB will have an expected number of points equal to 0.85 points.
If Henry plays the first game conservatively and the second game boldly, the following table gives the possible points earned and the probabilities (printed below the points).
Exercise 13.
What is the expected number of points that Henry will earn if he plays using a CB strategy?
Answer:
(1 \(\frac{1}{2}\))(0.36) + (1)(0.09) + (\(\frac{1}{2}\))(0.44) + (0)(0.11) = 0.85
Henry’s expected number of points won using the CB strategy is 0.85 points.
Exercise 14.
Of the four possible strategies, which should Henry play in order to maximize his expected number of points earned in a match?
Answer:
Henry’s best strategy is to play both games boldly (expected points = 0.9). Playing one game boldly and the other conservatively yields an expected 0.85 points, whereas playing both games conservatively is the least desirable strategy, 0.8 points.
Eureka Math Precalculus Module 5 Lesson 15 Problem Set Answer Key
Question 1.
A game allows you to choose what number cubes you would like to use to play. One pair of number cubes is a regular pair in which the sides of each cube are numbered from 1 to 6. The other pair consists of two different cubes as shown below. For all of these number cubes, it is equally likely that the cube will land on any one of its six sides.
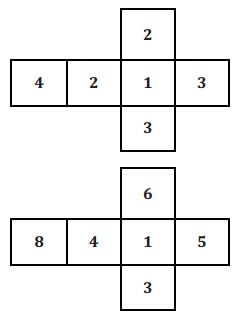
a. Suppose that you want to maximize the expected sum per roll in the long run. Which pair of number cubes should you use? Explain why.
Answer:
For the regular fair number cubes, the expected sum per roll is (2)(\(\frac{1}{36}\)) + (3)(\(\frac{2}{36}\)) + (4)(\(\frac{3}{36}\)) + (5)(\(\frac{4}{36}\)) + (6)(\(\frac{5}{36}\)) + (7)(\(\frac{6}{36}\)) + (8)(\(\frac{5}{36}\)) + (9)(\(\frac{4}{36}\)) + (10)(\(\frac{3}{36}\)) + (11)(\(\frac{2}{36}\)) + (12)(\(\frac{1}{36}\)) = 7.
For the Sicherman number cubes, first note that the distribution of the sum is (surprisingly) the same as that for the regular number cubes. The expected sum per roll is 7.
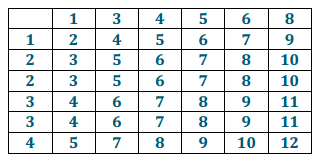
Since the expected sum per roll is 7 for each pair of cubes, you could choose either pair of number cubes.
b. Imagine that you are playing a game in which you earn special privileges by rolling doubles (i.e., the same number on both cubes). Which number cubes would you prefer to use? Explain.
Answer:
Students should then be able to suggest that the regular number cubes have 6 possible doubles, but the Sicherman number cubes have only 4. So, for games that have special rules for rolling doubles, the regular number cubes are preferable despite the fact that the expected sum per roll is the same for each type of cube.
Question 2.
Amy is a wedding planner. Some of her clients care about whether the wedding is held indoors or outdoors depending on weather conditions as well as respective costs. Over the years, Amy has compiled the following data for June weddings. (Costs are in thousands of dollars.)

a. What is the expected cost of a June wedding held indoors?
Answer:
Note: Be sure students check that the probabilities add to 1.
The expected cost of a June wedding held indoors is as follows: (29)(0.15) + (30)(0.05) + (22)(0.45) + (24)(0.35) = 24.15.
The expected cost of a June wedding held indoors is $24,150.00.
b. What is the expected cost of a June wedding held outdoors?
Answer:
The expected cost of a June wedding held outdoors is as follows: (33)(0.15) + (40)(0.05) + (27)(0.45) + (30)(0.35) = 29.60.
The expected cost of a June wedding help outdoors is $29,600.00.
c. A new client has her heart set on an outdoor wedding. She has at most $25,000.00 available. What do you think Amy told the client and why?
Answer:
Amy would have told her new client that she has enough money to cover an indoor wedding, as the expected cost is $24,150.00. However, no matter the weather conditions, the client will not be able to afford an outdoor wedding. The expected cost of an outdoor wedding (regardless of weather) is $29,600.00, so the client’s budget falls $4,600.00 short.
Question 3.
A venture capitalist is considering two investment proposals. One proposal involves investing $100,000.00 in a green alternative energy source. The probability that it will succeed is only 0.05, but the gain on investment would be $2,500,000.00. The other proposal involves investing $300,000.00 in an existing textile company. The probability that it will succeed is 0.5, and the gain on investment would be $725,000.00. In which proposal should the venture capitalist invest? Explain.
Answer:
The following are probability distributions for each proposal:

The expected gain for each proposal is as follows:
Green Energy: $0(0.95) + $2 500 000(0.05) = $125 000.00
Textile Company: $0(0.5) + $725 000(0.5) = $362 500.00
The venture capitalist’s expected profit can be found by subtracting the amount invested from the expected gain.
The expected profit from the green energy proposal is $125 000.00-$100 000.00, or $25,000.00.
The expected profit from the textile proposal is $362 500.00-$300 000.00, or $62,500.00.
The venture capitalist should invest in the textile company because the expected profit is higher.
Question 4.
A student is required to purchase injury insurance in order to participate on his high school football team.
The insurance will cover all expenses incurred if the student is injured during a football practice or game, but the student must pay a deductible for submitting a claim. There is also an up-front cost to purchase the injury insurance.
- Plan A costs $75.00 up front. If the student is injured and files a claim, the deductible is $100.00.
- Plan B costs $100.00 up front. If the student is injured and files a claim, the deductible is $50.00.
Suppose there is a 1 in 5 chance of the student making a claim on the insurance policy. Which plan should the student choose? Explain.
Answer:
The probability distributions for each plan are as follows:
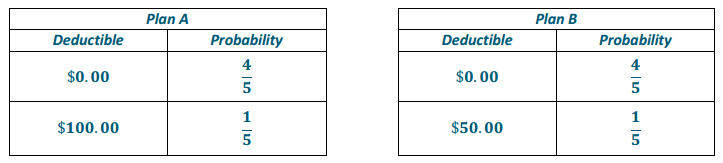
The expected cost of submitting a claim for each plan is as follows:
Plan A: $0(\(\frac{4}{5}\)) + $100(\(\frac{1}{5}\)) = $20.00
Plan B: $0(\(\frac{4}{5}\)) + $50(\(\frac{1}{5}\)) = $10.00
Because there is also an up-front cost to purchase the insurance policy, the up-front cost should be combined with the expected cost of submitting a claim to determine the total out-of-pocket expense for the student.
The expected total cost of Plan A is $20.00 + $75.00 or $95.00. The expected total cost of Plan B is
$10.00 + $100.00 or $110.00.
The student should choose Plan A in order to minimize his out-of-pocket expenses.
Eureka Math Precalculus Module 5 Lesson 15 Exit Ticket Answer Key
Question 1.
Your older sister asks you which of two summer job opportunities she should take. She likes them both. Job A is self-employed; Job B works with a friend. The probability distributions for the amount of money that can be earned per day, X, follow. In Job B, money earned will be split evenly between your sister and her friend.
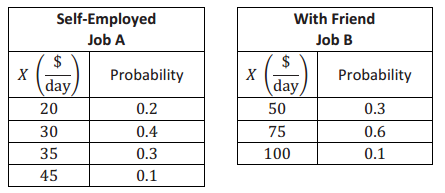
Which opportunity would you recommend that your sister pursue? Explain why in terms of expected value.
Answer:
(Be sure students first check that the probabilities add to 1 in each case.) Since your sister has no preference regarding the jobs, your recommendation should be based on expected earnings.
E(earnings for Job A) = (20)(0.2) + (30)(0.4) + (35)(0.3) + (45)(0.1) = 31
Your sister could expect to earn $31 per day from Job A.
E(earnings for Job B) = (50)(0.3) + (75)(0.6) + (100)(0.1) = 70
Your sister could expect to earn $70 per day for two people, or $35 each from Job B.
Recommend Job B because the expected earnings per day are $35, which is more than the expected earnings for Job A.
Question 2.
A carnival game consists of choosing to spin the following spinner once or roll a pair of fair number cubes once.
If the spinner lands on 0, you get no points; if it lands on 3, you get 3 points; if it lands on 6, you get 6 points. If the two number cubes sum to a prime number, you get 4 points. If the sum is not a prime number, you get 0 points. Should you spin the spinner or choose the number cubes if you want to maximize the expected number of points obtained? Explain your choice. Note: The spinner is broken up into wedges representing \(\frac{1}{2}\), \(\frac{1}{3}\), and \(\frac{1}{6}\).
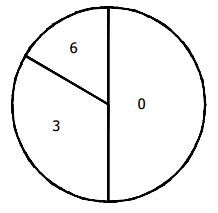
Answer:
(0)(\(\frac{1}{2}\)) + (3)(\(\frac{2}{6}\)) + (6)(\(\frac{1}{6}\)) = 2
The expected number of points spinning the spinner is 2 points.
(4)(\(\frac{15}{36}\)) = 1\(\frac{2}{3}\)
The expected number of points rolling the fair number cubes is 1 \(\frac{2}{3}\) points.
Spin the spinner because the expected number of points from spinning the spinner is slightly higher than the expected number of points from rolling the fair number cubes.