The statement “Every Diagonal of a Parallelogram Divides it into Two Triangles of Equal Area” is a property related to the area of the triangle and area of a parallelogram. By using the Every Diagonal of a Parallelogram Divides it into Two Triangles of Equal Area theorem the students of 9th grade can solve different types of problems related to the concept Area.
Also Read:
- Base and Height (Altitude) in a Triangle and a Parallelogram
- If Each Diagonal of a Quadrilateral Divides it in Two Triangles of Equal Area then Prove that the Quadrilateral is a Parallelogram
Every Diagonal of a Parallelogram Divides it into Two Triangles of Equal Area – Theorem
Statement:
Prove that Every Diagonal of a Parallelogram Divides it into Two Triangles of Equal Area.
Proof:
Here ABCD is a parallelogram and BD is diagonal
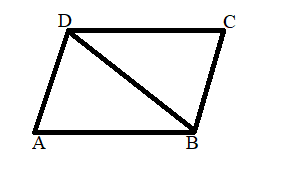
In ∆ADB and ∆CBD
AD // BC
∠ADB = ∠CBD( alternate angles )
Also AB // DC
∠ABD = ∠CDB( alternate angles )
DB = BD
Therefore ∆ADB ≅ ∆CDB( by SAS congruence rule)
Since congruent figures have the same area
ar(ADB) = ar(CBD)
Hence proved.
FAQs on A Diagonal Divides a Parallelogram into Two Triangles of Equal Area
1. What divides a parallelogram into two triangles of equal area?
The diagonal divides a parallelogram into two triangles of equal area.
2. Are the opposite sides of a parallelogram always equal?
opposite sides of a parallelogram are equal. The diagonals of a parallelogram bisect each other. Each diagonal of a parallelogram bisects into two congruent triangles.The quadrilateral is a parallelogram.
3. Do all parallelograms have 4 equal sides?
A parallelogram has two parallel pairs of opposite sides. A rectangle has two pairs of opposite sides parallel, and it has four right angles. It is also a parallelogram and it has two pairs of parallel sides. A square has two pairs of parallel sides, four right angles, and all four sides are equal.