Check Expressing Numbers in the Expanded Form Problems and concept. Know the various positions of a number and how it expands according to the positions of the number. Know the definition, fun facts, example problems of various numbers like decimal numbers, natural numbers, etc.
Also, See: Expressing Numbers on the Number Line
Expressing Numbers in the Expanded Form
Expanded Form will be represented as the way of expressing the numbers which show each digit value. It helps us to understand the number in a better way. For example, consider the number 21656362798. For this number, it is difficult to understand, hence the expanded form helps us in giving a better understanding of the number.
Now, we consider the simple number which is 632, and give its expanded form. 632 is noted in the expanded form as 600 + 30 + 2 which means that there will be 6 hundred, 3 tens, and 2 ones. Hence, the meaning of the number can be easily understood. To understand the higher number of digits, it is really difficult to know it without the expanded form. The digits in the number will be written in the forms of 1, 10, 100, 1000, etc.
Pictorial Representation of Expansion of a number
Suppose that a number is 943. To easily understand how it is read we will see the below pictorial representation and how each digit is divided into a number. 943 s divided into 9 blocks of hundred, 4 blocks of tens, and 3 blocks of ones.
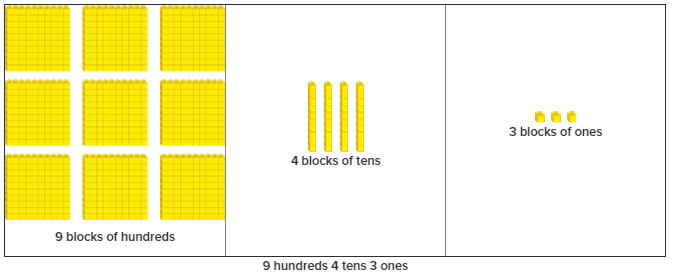
Expanded Form: 900 + 40 + 3
How to Write Numbers in Expanded Form?
Each digit of the number has a place value which determines its value according to the position in that number. The digit value increases as the number moves from left to right. The digits on the right have a higher place value compared to the digits which are present on the left side.
Step 1: In the first step, note the number and count the number of digits.
Step 2: In this step, you have to determine the place values of the digits with the help of the place chart value
Step 3: Now, after determining the place values, multiply the number with place values
Step 4: Then, you have to show it as digit * place value
Step 5: In the final step, represent all the digits as the digit and its place value product
Expanded Form of Decimal Numbers
Same as whole numbers, decimal values or numbers can be written in the expanded form. To write the decimals in the expanded form, we have to multiply each decimal digit with exponent values increment of (1/10). We will see the expansion of decimal numbers with the simple example.
Suppose that the decimal number is 0.687 will be written in the expanded form like 6 * (1/10) + 8 * (1/10)2 + 7 * (1/10)3 which can also be written as 6 * (1/10) + 8 * (1/100) + 7 * (1/1000) = 0.6 + 0.08 + 0.007.
Therefore, the decimal numbers can easily be expressed in the expanded form. If the number is a fraction of a percentage value, then it must be converted to the decimal value which can be written in the expanded form.
Fun Facts about Expansion Forms
Expanded Form and expanded notations are not similar. The expanded notation is represented as the number where the sum of each digit is multiplied by its place value.
Expanded Form: 646 = 600 + 40 + 6
Expanded Notation: 646 = (6 100) + (4 10) + (6 1)
Only addition is used in the expanded forms between the place value numbers and we use Multiplication and Addition between the place values in the expanded notation.
Writing Numbers In Expanded Form Examples
Problem 1:
Express the number “97452” in the expanded form?
Solution:
The given number is 97452
It can be written as 9 Ten Thousands + 7 Thousands + 4 Hundreds + 5 Tens + 2 Ones
which is 9 * 10000, 7 * 1000, 4 * 100, 5 * 10, 2 * 1
= 9 * 10000 + 7 * 1000 + 4 * 100 + 5 * 10 + 2 * 1
= 90000 + 7000 + 400 + 50 + 2
Therefore, the expanded form of the number “97452” is 90000 + 7000 + 400 + 50 + 2
Hence, the final solution is 90000 + 7000 + 400 + 50 + 2
Problem 2:
Express the number “1234.56” in the expanded form?
Solution:
The given number is “1234.56”
It can be written as 1 Thousands, 2 Hundreds, 3 Tens, 4 Ones, One by tenth of 5, One by Hundreths of 6
which is 1 * 1000, 2 * 100, 3 * 10, 4* 1, 5/10, 6/100
= 1 * 1000 + 2 * 100 + 3 * 10 + 4 * 1 + 5/10 + 6/100
= 1000 + 200 + 30 + 4 + 5/10 + 6/100
Therefore, the expanded form of the number “1234.56” is 1000 + 200 + 30 + 4 + 5/10 + 6/100
Hence, the final solution is 1000 + 200 + 30 + 4 + 5/10 + 6/100
Problem 3:
Express the number “56,298” in the expanded form?
Solution:
The given number is 56,298
It can be written as
The 5 is in the ten thousands place, equalling 50,000
The 6 is in thousands place, equalling 6000
The 2 is in hundreds place, equalling 200
The 9 is in tens place, equalling 90
The 8 is in ones place, equalling 8
which is 5 * 10000, 6 * 1000, 2 * 100, 9 * 10, 8 * 1
= 5 * 10000 + 6 * 1000 + 2 * 100 + 9 * 10 + 8 * 1
= 50,000 + 6000 + 200 + 90 + 8
Therefore, the expanded form of the number “56,298” is 50,000 + 6000 + 200 + 90 + 8
One thing that we need to be careful with the expansion of numbers is when the number has zero included in it.
Problem 4 :
Consider a number “548,029” and express it in the expanded form?
Solution:
The given number “548,029”
As there is zero included in the number, we do not consider its place value instead add zero in that place and write other places as they are.
It can be written as,
The 5 is in the ten thousand place, equalling 50,000
The 4 is in the thousands place, equalling 4000
The 8 is in the hundreds place, equalling 800
Zero is in tens place, but we do not consider its place value as a number multiplied by zero is zero
The 2 is in tens place, equalling 20
The 9 is in ones place, equalling 9
which is 5 * 10000, 4 * 1000, 8 * 100, 0, 2 * 10, 9 * 1
= 5 * 10000 + 4 * 1000 + 8 * 100 + 0 + 2 * 10 + 9 * 1
= 50000 + 4000 + 800 + 20 + 9
Therefore, the expanded form of the number “54,829” is 50000 + 4000 + 800 + 20 + 9
Thus, the final solution is 50000 + 4000 + 800 + 20 + 9