Four Triangles which are Congruent to One Another: Initially, you should aware of the congruence of triangles as it aids you to perceive the concept of congruence from a different point of view. The meaning of congruence in mathematics is when two figures are similar to each other based on their shape and size. The term congruence is used to specify an object and its mirror image. Two objects are said to be congruent if they lie over each other.
Let us discuss the congruency of triangles and also three line segments that join the middle points of the sides of a triangle, and divide it into four triangles that are congruent to one another. From here you can view the statement and how to prove that the four triangles formed by joining in pairs, the mid-points of three sides of a triangle, are congruent to each other.
Do Check:
Congruent – Definition & Meaning
In mathematics, the word congruent means ‘exactly equal’ in terms of size and shape, and it is also defined as those figures and shapes that can be flipped or rotated and slide they remained to be consistent with the other shapes. All shapes can be reflected to concur with similar shapes.
Two sizes or shapes are congruent if they have only the same size and shape. In other words, two triangles are said to be congruent if pairs of their corresponding sides and their corresponding angles are equal.
Congruency of Triangles
A triangle is a polygon made of three line segments forming with three angles. Congruence in two or more triangles depends on the measurements and length of their sides and angles, the three sides of a triangle define its size and the three angles of a triangle define its shape and then the triangles are said to be congruent.
Therefore, two triangles are superimposed side to side and angle to angle. The symbol is used to denote the congruency in triangles is ” ≅”.
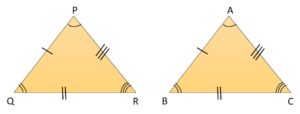
In the above figure, the triangles PQR and ABC are congruent to each other. Symbolically, we write as ΔPQR ≅ ΔABC.
Statement
The line segments joining the middle points of the sides of a triangle are divided into four triangles and are congruent to each other.
Prove:
Here we will show the three line segments D, E, and F joining the middle points and forming four triangles of a ΔABC that are congruent to one another respectively.
ΔAFE ≅ ΔFBD ≅ ΔEDC ≅ ΔDEF
Construction:
Now, we construct the triangle ABC with the midpoints D, E, and F respectively.

Proof:
The line segments joining the sides of a triangle are half to the third side by midpoint theorem. D, E, and F are midpoints of BC, AC, and AB respectively.
DE = ½AB ⇒ DE = AF = BF → (1)
EF = ½BC ⇒ EF = BD = CD → (2)
DF = ½AC ⇒ DF = AE = EC → (3)
Now in ΔDEF and ΔAFE
DE = AF
DF = AE
EF= FE
So, by SSS theorem of congruence
ΔDEF ≅ ΔAFE.
Similarly,
ΔDEF ≅ ΔFBD and ΔDEF ≅ ΔEDC
Therefore,
ΔAFE ≅ ΔFBD ≅ ΔEDC ≅ ΔDEF.
Hence, four triangles formed by joining the midpoints of a triangle are congruent to each other.
Examples of Four Triangles which are Congruent to One Another
Example 1:
If two triangles ABC and DEF have the measurements such that, AB=4.5 cm, BC=2.1 cm, AC=3 cm, DE=2.1 cm, EF=4.5 cm, and DF=3 cm. Find the triangles ABC and DEF are congruent to each other or not?
Solution:
Given ΔABC and ΔDEF
AB = EF = 4.5 cm,
BC = DE = 2.1 cm, and
AC = DF = 3 cm
By SSS theorem of congruence,
ΔABC ≅ ΔDEF
Hence, both the triangles are congruent to one another.
Example 2:
Prove that the given triangles are congruent triangles or not based on the rule of congruence.
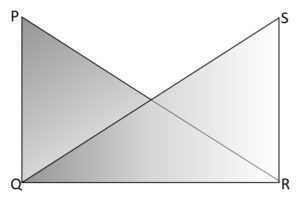
Solution:
In ΔPQR and ΔSRQ,
Let us try to notice any three parts of one triangle equal to the corresponding parts of the other triangle.
Now, we find that PQ = SR, PR = SQ, and QR are the common line segment for both the triangles.
Thus, by SSS rule of congruence, ΔPQR and ΔSRQ are congruent triangles.
Therefore, ΔPQR ≅ ΔSRQ.
Example 3:
Identify the type of congruence in two triangles given
∆ABC, AB=5 cm, BC=4 cm, ∠B=40° and ∆DEF, DE=4 cm, EF=5 cm, ∠E=40°.
Solution:
Given ∆ABC and ∆DEF
AB = EF = 5 cm,
BC = DE = 5 cm, and
∠B = ∠E =40°.
By SAS rule of congruency,
∆ABC ≅ ∆DEF.
FAQs on Congruent Triangles in Maths
1. What are congruent triangles?
Two triangles are said to be congruent if all the three corresponding sides and all the three corresponding angles are equal in size and measure.
2. How to prove that the four triangles are congruent or not?
By the rule of Angle-Side-Angle, you can easily prove that the four triangles formed by joining in pairs, the mid-points of three sides of a triangle, are congruent to each other. If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, then the triangles are congruent.
3. What are the rules applied for congruency?
The rules applied for congruent triangles are as follows:
(i) SSS Criterion: Side-Side-Side
(ii) SAS Criterion: Side-Angle-Side
(iii) ASA Criterion: Angle-Side-Angle
(iv) AAS Criterion: Angle-Angle-Side
(v) RHS Criterion: Right angle- Hypotenuse-Side