Fraction as Division is the representation of fractions as division rule (÷). You can convert any fraction to division with the simple steps provided. By dividing the numerator (upper part of the fraction) with the denominator (lower part of the fraction) can get you the division.
Check the detailed explanation of the concept of fraction as division on this page. For a better understanding of the division concept with fractions, we have listed all of them explaining step by step along with images in the next sections.
Example:
\(\frac {6}{5} \) = 6 ÷5
How to Interpret a Fraction as Division?
You can convert the Fractions into Divisions by using the division rule. Firstly, find out the numerator and denominator of the fraction. Then, use the division symbol to show the fraction as the division. If you wish to simplify, you can simplify the division.
Fractions Expressed as Division
Check out the below examples to find out the examples of Fractions Expressed as Division.
(i) 11/9 = 11 ÷ 9
(ii) 5/13 = 5 ÷ 13
(iii) 92/65 = 92 ÷ 65
(iv) 3/7 = 3 ÷ 7
(v) 16/19 = 16 ÷ 19
Divisions Expressed as Fractions
Find the below examples to find out the Divisions Expressed as Fractions examples.
(i) 10 ÷ 4 = 10/4;
(ii) 14 ÷ 6 = 14/6
(iii) 7 ÷ 5 = 7/5
(iv) 17 ÷ 7 = 17/7
(v) 13 ÷ 21 = 13/21
See More:
- Conversion of Improper Fractions into Mixed Fractions
- Interesting Fact about Equivalent Fractions
- Representing Fractions on Number Line
Fractions as Division Problems
We have given different examples with explanations and images below.
Example 1:
Raju has 2 packets of biscuits and each of the packets has 9 biscuits. He wants to divide the two packets of biscuits into 3. How many biscuits will each packet contain when divided into 3 packets?
Solution:
Raju has 18 biscuits with him.
He wants to divide it into 3 packets.
We can show the division with a fraction as follows:
18 ÷ 3 which is a fraction
On further simplification of fraction, we get the result as 6.
Therefore, when divided into 3 packets, each of the packets contain 6 biscuits.
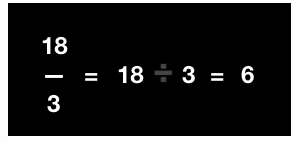
Example 2:
Suppose that there are 64 chocolates in the box. We have to pack them into 4 boxes. Thus many chocolates do each box contains and how do you represent them in the form of fractions?
Solution:
Given that the No of total chocolates in a box = 64
No of boxes these chocolates are to be divided = 4
The total no of chocolates in each box can be represented with fractions i.e., \(\frac {64}{4} \) = 64 ÷ 4
On further division, we get the result as 16
Therefore, there are 16 chocolates in each box.
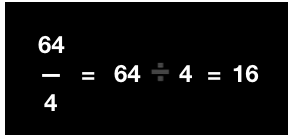
Example 3:
There are 96 cupcakes in a box. 12 cupcakes are to be packed in each box. How many boxes do we need?
Solution:
Given that the total no of cupcakes in a box = 96
No of cupcakes to be packed in each box = 12
The total no of boxes can be represented with fractions i.e., \(\frac {96}{12} \) = 96 ÷12
On further division, we get the result as 8
Therefore, 8 boxes are needed to pack 96 cupcakes.
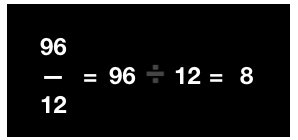
Example 4:
2496 nails are packed into 6 boxes. Find the number of nails in each box?
Solution:
Given that the total no of nails = 2496
No of boxes = 6
Total no of nails in each box can be represented with fractions i.e., \(\frac {2496}{6} \) = 2496 ÷ 6
On further division, we get the result as 416
Therefore, 416 nails are there in each box.
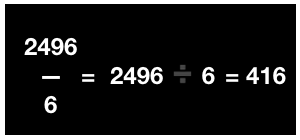
Example 4:
176 bottles should be placed in 8 trays. Find the number of bottles in each tray?
Solution:
Given that the total number of bottles = 176
No of trays = 8
Total number of bottles in each tray can be represented with fractions i.e., \(\frac {176}{8} \) = 176 ÷ 8
On further division, we get the result as 22
Therefore, 22 bottles should be placed in each tray.
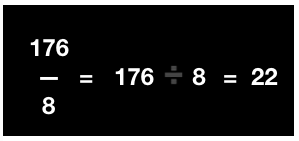
Example 5:
4404 boxes of oranges should be placed in 6 trucks. Find the total number of boxes placed in each truck?
Solution:
Given that the total no of boxes of oranges = 4404
No of trucks = 6
The total no of boxes placed in each truck can be represented with fractions i.e., \(\frac {4404}{6} \) = 4404 ÷ 6
On further division, we get the result as 734
Therefore, 734 boxes are to be placed in each truck.

FAQs on Understanding Fractions as Division
1. How to convert fractions as division?
To convert the fractions as division, use the calculator and divide the upper part of the fraction (numerator) by the bottom part of the fraction (denominator).
2. Give an example of fractions as division?
Suppose that \(\frac {3}{4} \) is the fraction, then write the numerator “3” followed by the division symbol and then followed by “4”.
Division of \(\frac {3}{4} \) is 3 ÷ 4
3. Arefractions as division and division of fractions the same?
The answer is no. Fractions as division are the representation of fractions as division rules (÷). Division of fractions represents breaking down the fraction into further parts.