Are you viewing for Go Math Grade 4 Answer Key Homework Practice FL Chapter 13 Algebra: Perimeter and Area? This is the correct page for you. We have listed chapterwise Go math grade 4 practice FL Answer key along with homework practice FL solution Key on our site. So, you can learn the concepts in an understanding manner & score maximum scores in the assessments and standardized tests. Hence, download the HMH Go Math 4th Grade Chapter 13 Perimeter and Area Answer key to find out the area & perimeter of the rectangle & square quickly & easily.
Go Math Grade 4 Answer Key Homework Practice FL Chapter 13: Algebra: Perimeter and Area
Go Math Grade 4 Ch 13 Answer Key includes topics covered in Algebra: Perimeter and Area. Students who are pursuing 4th grade can find the HMH Go Math Grade 4 Solution Key Chapter 13 Algebra: Perimeter and Area extremely useful. Simply identify your preparation level and weak areas by practicing and solving the questions from 4th Grade Go Math Answer Key Chapter 13 Algebra: Perimeter and Area. Tap on the below provided links and check the detailed explanation for each and every question covered here.
Lesson: 1 – Perimeter
- Common Core – Algebra: Perimeter and Area – Page No. 247
- Common Core – Algebra: Perimeter and Area – Page No. 248
Lesson: 2 – Area
- Common Core – Algebra: Perimeter and Area – Page No. 249
- Common Core – Algebra: Perimeter and Area – Page No. 250
Lesson: 3 – Area of Combined Rectangles
- Common Core – Algebra: Perimeter and Area – Page No. 251
- Common Core – Algebra: Perimeter and Area – Page No. 252
Lesson: 4 – Find Unknown Measures
- Common Core – Algebra: Perimeter and Area – Page No. 253
- Common Core – Algebra: Perimeter and Area – Page No. 254
Lesson: 5 – Problem Solving Find the Area
- Common Core – Algebra: Perimeter and Area – Page No. 255
- Common Core – Algebra: Perimeter and Area – Page No. 256
Lesson: 6
- Common Core – Algebra: Perimeter and Area – Page No. 257
- Common Core – Algebra: Perimeter and Area – Page No. 258
Common Core – Algebra: Perimeter and Area – Page No. 247
Perimeter
Find the perimeter of the rectangle or square.
Question 1.
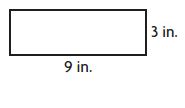
9 + 3 + 9 + 3 = 24
24 inches
Question 2.
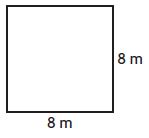
_____ meters
Answer: 32
Explanation:
Given,
sides = 8 m
we know that the perimeter of a square is 4×s
P = 4 × s
P = 4 × 8m
P = 32m
Therefore the perimeter of the above square is 32m
Question 3.
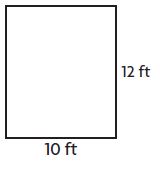
_____ feet
Answer: 44
Explanation:
Given,
Length (L) = 10 ft
Width (W) = 12 ft
we know that the perimeter of a Rectangle is L + L+ W + W
P = L + L+ W + W
P = 10 ft + 10 ft + 12 ft + 12 ft
P = 44 ft
Therefore the perimeter of the above Rectangle is 44 ft
Remember: The perimeter is the total distance around the outside, which can be found by adding together the length of each side. In the case of a rectangle, opposite sides are equal in length, so the perimeter is twice its width plus twice its height.
Question 4.
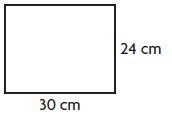
____ centimeters
Answer: 108
Explanation:
Given,
Length (L) = 30 cm
Width (W) = 24 cm
we know that the perimeter of a Rectangle is L + L+ W + W
P = L + L+ W + W
P = 30 cm + 30 cm + 24 cm + 24 cm
P = 108 cm
Therefore the perimeter of the above Rectangle is 108 cm
Question 5.

____ inches
Answer: 216
Explanation:
Given,
Length (L) = 25 in.
Width (W) = 83 in.
we know that the perimeter of a Rectangle is L + L+ W + W
P = L + L+ W + W
P = 25 in. + 25 in. + 83 in. + 83 in.
P = 216 in.
Therefore the perimeter of the above Rectangle is 216 in.
Question 6.
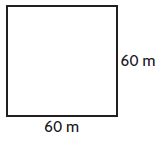
_____ meters
Answer: 240
Explanation:
Given,
sides = 60 m
we know that the perimeter of a square is 4×s
P = 4×s
P = 4×60 m
P = 240 m
Therefore the perimeter of the above square is 240 m
Problem Solving
Question 7.
Troy is making a flag shaped like a square. Each side measures 12 inches. He wants to add ribbon along the edges. He has 36 inches of ribbon. Does he have enough ribbon? Explain.
_____
Answer: no. He needs 48 inches of ribbon.
Explanation:
Since each side is 12 inches, then multiply 12 by 4 since it’s a square and has 4 sides which make 48.
48 is bigger than 36.
Therefore, Troy does not have enough ribbon.
Question 8.
The width of the Ochoa Community Pool is 20 feet. The length is twice as long as its width. What is the perimeter of the pool?
_____ feet
Answer: 120
Explanation:
Width of the Ochoa community pool = 20 feet
Length is twice as long as its width = 2(20) = 40 feet
Use this formula to get perimeter = 2(w) + 2(L)
then the perimeter equals to = 2(20)+ 2(40)
P = 40 feet + 80 feet = 120 feet
Therefore The perimeter of the pool is 120 feet.
Common Core – Algebra: Perimeter and Area – Page No. 248
Lesson Check
Question 1.
What is the perimeter of a square window with sides 36 inches long?
Options:
a. 40 inches
b. 72 inches
c. 144 inches
d. 1,296 inches
Answer: 144 inches
Explanation:
Perimeter of a square = L + L + L + L = 4L
From the question given L=36 inches
substitute the value of L into the formula
Perimeter of a square (P)= L + L + L + L
P = 36 in. + 36 in.. +36 in.+ 36 in.
P =144 inches
Therefore the perimeter of a square window with sides 36 inches long is 144 inches.
Question 2.
What is the perimeter of the rectangle below?
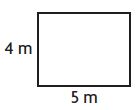
Options:
a. 11 meters
b. 14 meters
c. 18 meters
d. 400 meters
Answer: 18 meters
Explanation:
Given,
Length (L) = 5 m
Width (W) = 4 m
we know that the perimeter of a Rectangle is L + L+ W + W
P = L + L+ W + W
P = 5 m + 5 m + 4 m + 4 m
P = 18 m
Therefore the perimeter of the above Rectangle is 18 m
Thus the correct answer is option c.
Spiral Review
Question 3.
Which is the most reasonable estimate for the measure of the angle Natalie drew?
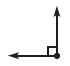
Options:
a. 30°
b. 90°
c. 180°
d. 210°
Answer: 90°
Explanation:
Right angle: An angle of 90°, as in a corner of a square or at the intersection of two perpendicular straight lines.
As we can see in the figure, that an angle is made at the intersection of the two perpendicular straight lines, thus the figure will be definitely a right-angled figure.
Therefore, the measure of the angle Natalie draw is 90°.
Thus the correct answer is option b.
Question 4.
Ethan has 3 pounds of mixed nuts. How many ounces of mixed nuts does Ethan have?
Options:
a. 30 ounces
b. 36 ounces
c. 48 ounces
d. 54 ounces
Answer: 48 ounces
Explanation:
Since we have given that
Number of pounds of mixed nuts = 3
As we know that
1 pound = 16 ounces
So, we need to find the number of ounces of mixed nuts Ethan has.
So, the number of ounces of mixed nuts Ethan have is given by
= 3 × 16
= 48 ounces
Thus the correct answer is option c.
Question 5.
How many lines of symmetry does the shape below appear to have?
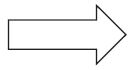
Options:
a. 0
b. 1
c. 2
d. more than 2
Answer: 1
Explanation:
It has only one line of symmetry on the horizontal axis because it is an arrow.
Thus the correct answer is option b.
Question 6.
Which of the following comparisons is correct?
Options:
a. 0.70 > 7.0
b. 0.7 = 0.70
c. 0.7 < 0.70
d. 0.70 = 0.07
Answer: 0.7 = 0.70
The decimal 0.7 and 0.70 are the same so the correct answer is option b.
Common Core – Algebra: Perimeter and Area – Page No. 249
Area
Find the area of the rectangle or square.
Question 1.
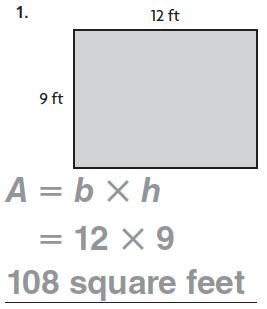
Answer: 108 Square feet
Explanation:
Given,
Height (h) = 9 ft.
Breath (b) = 12 ft.
Area of the rectangle A = b×h
A = 12 ft × 9 ft
A = 108 Square feet.
Therefore the Area of the rectangle is 108 Square feet.
Question 2.
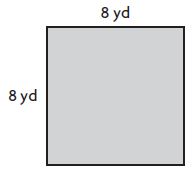
_____ square yards
Answer: 64
Explanation:
Given,
Sides (s) = 8 yd
Area of the square. A = s×s
A = 8 yd × 8 yd
A = 64 Square yards
Therefore the Area of the square is 64 Square yards.
Question 3.
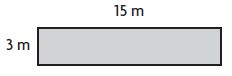
______ square meters
Answer: 45
Explanation:
Given,
Height (h) = 3 m
Breath (b) = 15 m
Area of the rectangle or square. A = b×h
A = 3 m× 15 m
A = 45 Square meters
Therefore the Area of the rectangle is 45 Square meters
Question 4.
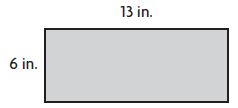
______ square inches
Answer: 78
Explanation:
Given,
Height (h) = 6 in.
Breath (b) = 13 in.
Area of the rectangle = A = b×h
A = 6 in. × 13 in.
A = 78 square inches
Therefore the Area of the rectangle is 78 square inches.
Question 5.
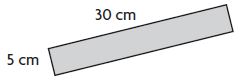
______ square centimeters
Answer: 150 square cm
Explanation:
Given,
Height (h) = 5 cm
Breath (b) = 30 cm
Area of the rectangle or square. A = b×h
A = 5 cm × 30 cm
A = 150 square centimeters
Therefore the Area of the rectangle is 150 square centimeters.
Question 6.
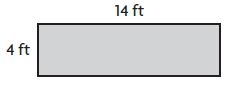
______ square feet
Answer: 56 square ft
Explanation:
Given,
Height (h) = 4 ft
Breath (b) = 14 ft
Area of the rectangle or square. A = b×h
A = 4 ft × 14 ft
A = 56 square feet
Therefore the Area of the rectangle is 56 square feet.
Problem Solving
Question 7.
Meghan is putting wallpaper on a wall that measures 8 feet by 12 feet. How much wallpaper does Meghan need to cover the wall?
_____ square feet wallpaper
Answer: 96 square feet wallpaper
Explanation:
Given,
Length = 8 feet.
Width = 12 feet.
the area (area=length × width)
area=8 × 12
area=96 square feets.
Therefore the area is always expressed in units squared it would be 96 square feet of wallpaper.
Question 8.
Bryson is laying down sod in his yard to grow a new lawn. Each piece of sod is a 1-foot by 1-foot square. How many pieces of sod will Bryson need to cover his yard if his yard measures 30 feet by 14 feet?
_____ pieces
Answer: 420 pieces
Explanation:
Given,
length (l) = 30 ft
Breath (b) = 14 ft
Area of the rectangle or square. A = l×b
A = 30 ft × 14 ft
A = 420
Therefore 420 pieces of sod will Bryson need to cover his yard if his yard measures 30 feet by 14 feet.
Common Core – Algebra: Perimeter and Area – Page No. 250
Lesson Check
Question 1.
Ellie and Heather drew floor models of their living rooms. Ellie’s model represented 20 feet by 15 feet. Heather’s model represented 18 feet by 18 feet. Whose floor model represents the greater area? How much greater?
Options:
a. Ellie; 138 square feet
b. Heather; 24 square feet
c. Ellie; 300 square feet
d. Heather; 324 square feet
Answer: Heather; 24 square feet
Explanation:
Given,
Ellie’s model represented 20 feet by 15 feet.
Heather’s model represented 18 feet by 18 feet.
Length of Ellie’s model = 20 feet
Width of Ellie’s model = 15 feet
Area = Length × Breadth
A = 20 × 15
A = 300 ft²
Length of Heather’s model = 18 feet
Width of Heather’s model = 18 feet
Area = Length × Breadth
A= 18 × 18
A= 324 ft²
Therefore Heather’s model has a greater area by (324-300)= 24 sq.ft.
Thus the correct answer is option b.
Question 2.
Tyra is laying down square carpet pieces in her photography studio. Each square carpet piece is 1 yard by 1 yard. If Tyra’s photography studio is 7 yards long and 4 yards wide, how many pieces of square carpet will Tyra need?
Options:
a. 10
b. 11
c. 22
d. 28
Answer: 28
Explanation:
Given,
Tyra’s photography studio length is 7 yards
Tyra’s photography studio width is 4 yards
Area = Length × Breadth
Area = 7 yards × 4 yards
Area = 28 square yards
Therefore as Each square carpet piece is 1 yard by 1 yard. No.of pieces of square carpet Tyra needed is 28.
Thus the correct answer is option d.
Spiral Review
Question 3.
Typically, blood fully circulates through the human body 8 times each minute. How many times does blood circulate through the body in 1 hour?
Options:
a. 48
b. 240
c. 480
d. 4,800
Answer: 480
Explanation:
Given,
blood fully circulates through the human body 8 times each minute
one hour = 60 minutes
blood circulates through the body in 1 hour = 8 times × 60 minutes.
= 480 Times.
Therefore blood circulates through the body in 1 hour is 480 times.
Thus the correct answer is option c.
Question 4.
Each of the 28 students in Romi’s class raised at least $25 during the jump-a-thon. What is the least amount of money the class raised?
Options:
a. $5,200
b. $700
c. $660
d. $196
Answer: $700
explanation:
If each of the 28 students made at least $25,
you would multiply 28 and 25 together to obtain the least amount of money the class raised.
That gets,
28×25 = 700.
Therefore The class made at least $700.
Thus the correct answer is option b.
Question 5.
What is the perimeter of the shape below if 1 square is equal to 1 square foot?
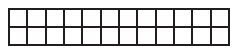
Options:
a. 12 feet
b. 14 feet
c. 24 feet
d. 28 feet
Answer: 28 feet
Explanation:
From the above figure we can observe that there area 2 rows and 12 columns.
L = 12 feet
W = 2 feet
We know that perimeter of the rectangle is 2l + 2w
P = 2l + 2w
P = 2(12) + 2(2)
P = 24 feet + 4 feet
P = 28 feet
Thus the correct answer is option d.
Question 6.
Ryan is making small meat loaves. Each small meat loaf uses \(\frac{3}{4 }\) pound of meat. How much meat does Ryan need to make 8 small meat loaves?
Options:
a. 4 pounds
b. 6 pounds
c. 8 pounds
d. 10 \(\frac{2}{3}\) pounds
Answer: 6 pounds
Explanation:
Given,
3/4 pound=1 small meatloaf
So Multiply 3/4 pound by 8
because he wants to make 8 small meatloaves.
= 3/4 × 8
= 24/4 (24 divided by 4)
= 6 pounds
Therefore Ryan need 6 pounds to make 8 small meat loaves.
Thus the correct answer is option b.
Common Core – Algebra: Perimeter and Area – Page No. 251
Area of Combined Rectangles
Find the area of the combined rectangles.
Question 1.
Question 2.
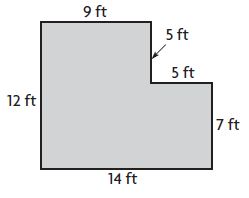
_____ square feet
Answer: 143
Explanation:
Divide the figure into two parts
Figure 1:
L = 9 ft
W = 5 ft
Area of the rectangle = l × w
A = 9 ft × 5 ft = 45 sq. ft
Figure 2:
L = 14 ft
W = 7 ft
Area of the rectangle = l × w
A = 14 ft × 7 ft = 98 sq. ft
Area of the combined rectangles = 98 sq. ft + 45 sq. ft = 143 sq. ft.
Question 3.
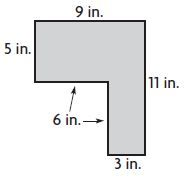
_____ square inches
Answer: 63
Explanation:
Divide the figure into two parts
Figure 1:
L = 9 in.
W = 5 in.
Area of the rectangle = l × w
A = 9 in. × 5 in. = 45 sq. in.
Figure 2:
L = 3 in.
W = 6 in.
Area of the rectangle = l × w
A = 3 in. × 6 in. = 18 sq. in.
Area of the combined rectangles = 45 sq. in + 18 sq. in = 63 square inches.
Question 4.
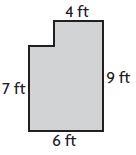
_____ square feet
Answer: 50 square feet
Explanation:
Divide the figure into two parts
Figure 1:
L = 4 ft
W = 2 ft
Area of the rectangle = l × w
A = 4 ft × 2 ft = 8 sq. ft
Figure 2:
L = 6 ft
W = 7 ft
Area of the rectangle = l × w
A = 6 ft × 7 ft = 42 sq. ft
Area of the combined rectangles = 8 sq. ft + 42 sq. ft = 50 sq. ft.
Question 5.
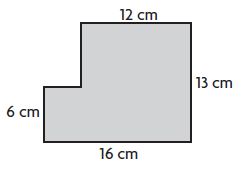
_____ square centimeters
Answer: 180 square centimeters
Explanation:
Divide the figure into two parts
Figure 1:
L = 12 cm
W = 7 cm
Area of the rectangle = l × w
A = 12 cm × 7 cm = 84 sq. cm.
Figure 2:
L = 16 cm
W = 6 cm
Area of the rectangle = l × w
A = 16 cm × 6 cm = 96 sq. cm
Area of the combined rectangles = 84 sq. cm + 96 sq. cm = 180 square centimeters
Question 6.
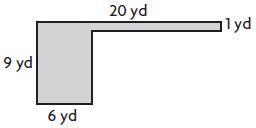
______ square yards
Answer: 68
Explanation:
Divide the figure into two parts
Figure 1:
L = 20 yd
W = 1 yd
Area of the rectangle = l × w
A = 20 yd × 1 yd = 20 sq. yd.
Figure 2:
L = 6 yard
W = 8 yard
Area of the rectangle = l × w
A = 6 yard × 8 yard = 48 sq. yard
Area of the combined rectangles = 20 sq. yd + 48 sq. yd = 68 square yards
Problem Solving
Use the diagram for 7–8.
Nadia makes the diagram below to represent the counter space she wants to build in her craft room.
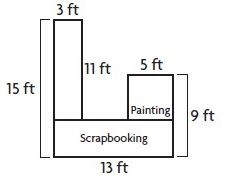
Question 7.
What is the area of the space that Nadia has shown for scrapbooking?
_____ square feet
Answer: 52
Explanation:
The length of the Scrapbooking is 13 ft
Width of the Scrapbooking is 4 ft
Area of the rectangle = l × w
A = 13 ft × 4 ft = 52 square feet
Thus the area of the space that Nadia has shown for scrapbooking is 52 square feet.
Question 8.
What is the area of the space she has shown for painting?
_____ square feet
Answer: 25
Explanation:
The area of the space shown for painting is square.
side = 5 ft
The area of the square is 5 ft × 5 ft = 25 sq. ft
Thus the area of the space she has shown for painting is 25 square feet.
Common Core – Algebra: Perimeter and Area – Page No. 252
Lesson Check
Question 1.
What is the area of the combined rectangles below?
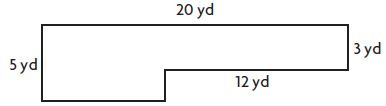
Options:
a. 136 square yards
b. 100 square yards
c. 76 square yards
d. 64 square yards
Answer: 76 square yards
Explanation:
Divide the figure into two parts
Figure 1:
L = 8 yd
W = 5 yd
Area of the rectangle = l × w
A = 8 yd × 5 yd = 40 sq. yd.
Figure 2:
L = 12 yard
W = 3 yard
Area of the rectangle = l × w
A = 12 yard × 3 yard = 36 sq. yard
Area of the combined rectangles = 40 sq. yd + 36 sq. yd = 76 square yards
Therefore the correct option is c.
Question 2.
Marquis is redecorating his bedroom. What could Marquis use the area formula to find?
Options:
a. how much space should be in a storage box
b. what length of wood is needed for a shelf
c. the amount of paint needed to cover a wall
d. how much water will fill up his new aquarium
Answer: the amount of paint needed to cover a wall
The correct answer is option c.
Spiral Review
Question 3.
Giraffes are the tallest land animals. A male giraffe can grow as tall as 6 yards. How tall would the giraffe be in feet?
Options:
a. 2 feet
b. 6 feet
c. 12 feet
d. 18 feet
Answer: 18 feet
Explanation:
Given,
Giraffes are the tallest land animals. A male giraffe can grow as tall as 6 yards.
we have to find How tall would the giraffe be in feet
Converting from Yards to feet.
one Yard = 3 Feet.
So 6 yards = 6 × 3 feet
= 18 feet
Therefore the correct option is d.
Question 4.
Drew purchased 3 books for $24. The cost of each book was a multiple of 4. Which of the following could be the prices of the 3 books?
Options:
a. $4, $10, $10
b. $4, $8, $12
c. $5, $8, $11
d. $3, $7, $14
Answer: $4, $8, $12
Explanation:
Given,
Drew purchased 3 books for $24. The cost of each book was a multiple of 4.
To find the prices of the 3 books
The cost of one book is $4
the cost of two books is $4 × 2 = $8
The cost of three books is $4 × 3 = $12
Therefore the correct option is b.
Question 5.
Esmeralda has a magnet in the shape of a square. Each side of the magnet is 3 inches long. What is the perimeter of her magnet?
Options:
a. 3 inches
b. 7 inches
c. 9 inches
d. 12 inches
Answer: 12 inches
Explanation:
Given,
Esmeralda has a magnet in the shape of a square.
Each side of the magnet is 3 inches long.
To find the perimeter of her magnet
P = 4 × s
P = 4 × 3 in.
P = 12 in.
Therefore the correct option is d.
Question 6.
What is the area of the rectangle below?
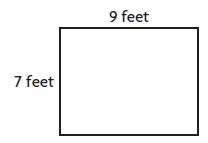
Options:
a. 63 square feet
b. 32 square feet
c. 18 square feet
d. 16 square feet
Answer: 63 square feet
Explanation:
Given,
Height (h) = 7 ft.
Breath (b) = 9 ft.
Area of the rectangle A = b×h
A = 7 ft × 9 ft
A = 63 Square feet.
The Area of the rectangle is 63 Square feet.
Therefore the correct option is a.
Common Core – Algebra: Perimeter and Area – Page No. 253
Find Unknown Measures
Find the unknown measure of the rectangle.
Question 1.
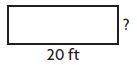
Perimeter = 54 feet
width = 7 feet
Think: P = (2 × l) + (2 × w)
54 = (2 × 20) + (2 × w)
54 = 40 + (2 × w)
Since 54 = 40 + 14, 2 × w = 14, and w = 7.
Question 2.
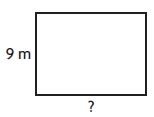
Perimeter = 42 meters
length = _____ meters
Answer: 12 meters
Explanation:
Given
Perimeter = 42 meters
width = 9 m
To find Length (l) of the rectangle
P = (2 × l) + (2 × w)
42 = (2 × l ) + (2 × 9)
42 = 2l + 18
2l = 42 – 18
2l = 24
l = 24/2
l = 12 m
Thus the length of the above rectangle is 12 m
Question 3.

Area = 28 square centimeters
height = _____ centimeters
Answer: 7 centimeters
Explanation:
Given
Area = 28 square centimeters
length = 4 cm
To find Height (w) of the rectangle
A = l × w
28 = 4 cm × w
w = 28/4
w = 7 cm
Thus the height of the above rectangle is 7 cm
Question 4.

Area = 200 square inches
base = _____ inches
Answer: 8 inches
Explanation:
Given
Area = 200 square inches
width = 25 in.
To find Base (b) of the rectangle
A = w × b
200 = 25 in. × b
b = 200/25
b = 8 inches
Thus the base of the above rectangle is 8 inches
Problem Solving
Question 5.
Susie is an organic vegetable grower. The perimeter of her rectangular vegetable garden is 72 yards. The width of the vegetable garden is 9 yards. How long is the vegetable garden?
length = _____ yards
Answer: 27 yards
Explanation:
Given,
The perimeter (P) of her rectangular vegetable garden is 72 yards.
The width (w) of the vegetable garden is 9 yards.
to find length (l)
P = (2 × l) + (2 × w)
72 yards = (2 × l ) + (2 × 9 yards)
72 = 2l + 18
2l = 72 – 18
2l = 54
l = 54/2
l = 27 yards
Therefore length = 27 yards
Question 6.
An artist is creating a rectangular mural for the Northfield Community Center. The mural is 7 feet tall and has an area of 84 square feet. What is the length of
the mural?
length = _____ feet
Answer: 12 feet
Explanation:
Given,
The mural is 7 feet (w) tall and has an area of 84 square feet(A).
To find the length (l)
A = l × w
84 = l × 7
l = 84 /7
l= 12 feets
Therefore the length is 12 feets
Common Core – Algebra: Perimeter and Area – Page No. 254
Lesson Check
Question 1.
The area of a rectangular photograph is 35 square inches. If the width of the photo is 5 inches, how tall is the photo?
Options:
a. 5 inches
b. 7 inches
c. 25 inches
d. 30 inches
Answer: 7 inches
Explanation:
Given,
The area of a rectangular photograph is 35 square inches (A)
The width of the photo is 5 inches (w)
To find how tall is the photo (l)
A= l × b
35 square in. = l × 5 in.
l = 35/5
l = 7 inches
Therefore the photo height is 7 inches.
Thus the correct answer is option b.
Question 2.
Natalie used 112 inches of blue yarn as a border around her rectangular bulletin board. If the bulletin board is 36 inches wide, how long is it?
Options:
a. 20 inches
b. 38 inches
c. 40 inches
d. 76 inches
Answer: 20 inches
Explanation:
Given width is 36 in and the total inches used was 112.
To find length
Perimeter of Rectangle = 2(L + W)
Your equation is, 2(L + 36) = 112
Solving for L:
2(L + 36) = 112
L + 36 = 112 / 2
L + 36 = 56
L = 56 – 36
L = 20
Therefore the correct option is a.
Spiral Review
Question 3.
A professional basketball court is in the shape of a rectangle. It is 50 feet wide and 94 feet long. A player ran one time around the edge of the court. How far did the player run?
Options:
a. 144 feet
b. 194 feet
c. 238 feet
d. 288 feet
Answer: 288 feet
Explanation:
Given, the basketball court is 50 feet wide and 94 feet long
The perimeter of the rectangle(P) is given by:
P = 2(length + width)
50 + 94 = 144
144 x 2 = 288
The player ran 288 feet
Therefore the correct option is d.
Question 4.
On a compass, due east is a \(\frac{1}{4}\) turn clockwise from due north. How many degrees are in a \(\frac{1}{4}\) turn?
Options:
a. 45°
b. 60°
c. 90°
d. 180°
Answer: 90°
Explanation:
We have been given that on a compass, due east is a 1/4 turn clockwise from due north.
Since we know that a compass is in form of a circle and the measure of degrees in a circle is 360 degrees.
To find the number of degrees in a one-fourth turn, we will divide 360° by 4.
Number of degrees in a 1/4 turn of compass = 360°/4
Number of degrees in a 1/4 turn of compass = 90°
Therefore, there are 90 degrees in a 1/4 turn of the compass.
The correct option is c.
Question 5.
Hakeem’s frog made three quick jumps. The first was 1 meter. The second jump was 85 centimeters. The third jump was 400 millimeters. What was the total length of the frog’s three jumps?
Options:
a. 189 centimeters
b. 225 centimeters
c. 486 centimeters
d. 585 millimeters
Answer: 225 centimeters
Explanation:
Given:
distance of first jump = d1= 1 meter
distance of second jump = d2 = 85 centimeters
distance of third jump = d3 = 400 millimeters
This problem is about the conversion unit of length.
We have to recall that :
1 m = 100 cm
1 m = 1000 mm
Total distance = d = d1 + d2 + d3
d = 1 m + 85 m + 400 mm
d = 1 m + 85/100 m + 400/1000 m
d = 2.25 × 100 cm
d = 225 centimeters
Therefore the correct option is b.
Question 6.
Karen colors in squares on a grid. She colored \(\frac{1}{8}\) of the squares blue and \(\frac{5}{8}\) of the squares red. What fraction of the squares are not colored in?
Options:
a. \(\frac{1}{8}\)
b. \(\frac{1}{4}\)
c. \(\frac{1}{2}\)
d. \(\frac{3}{4}\)
Answer: \(\frac{1}{4}\)
Explanation:
since karen colored in 1/8 and 5/8 you add the numerators to get 6/8 you subtract the 8/8 the whole grid from 6/8 to get 2/8
⇒ 1/8 + 5/8 = 6/8
⇒ 8/8 – 6/8 = 2/8
= 1/4
There fore the correct option is b.
Common Core – Algebra: Perimeter and Area – Page No. 255
Problem Solving Find the Area
Solve each problem.
Question 1.
A room has a wooden floor. There is a rug in the center of the floor. The diagram shows the room and the rug. How many square feet of the wood floor still shows?
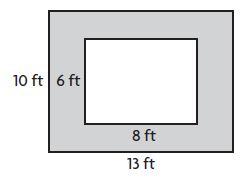
82 square feet
Area of the floor: 13 × 10 = 130 square feet
Area of the rug: 8 × 6 = 48 square feet
Subtract to find the area of the floor still showing: 130 – 48 = 82 square feet
Question 2.
A rectangular wall has a square window, as shown in the diagram.
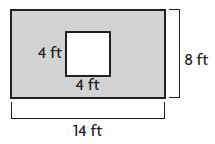
What is the area of the wall NOT including the window?
The area of the wall NOT including the window = _____ square feet
Answer: 96 square feet
Explanation:
The area of the square window is 4 ft × 4 ft = 16 square feet.
Area of the rectangle = 14 ft × 8 ft = 112 square feet
Now we have to find the area of the wall NOT including the window
112 square feet – 16 square feet = 96 square feet
Thus the area of the wall NOT including the window is 96 square feet.
Question 3.
Bob wants to put down new sod in his backyard, except for the part set aside for his flower garden. The diagram shows Bob’s backyard and the flower garden.
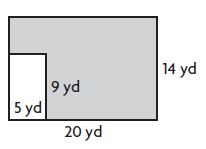
How much sod will Bob need?
The area covered with new sod = _____ square yards
Answer: 235 square yards
Explanation:
The area of the non-shaded rectangle is 5 yd × 9 yd = 45 square yards.
The area of the rectangle is 20 yd × 14 yd = 280 square yard
The area covered with new sod is 280 square yard – 45 square yard = 235 square yards.
Question 4.
A rectangular painting is 24 inches wide and 20 inches tall without the frame. With the frame, it is 28 inches wide and 24 inches tall. What is the area of the frame not covered by the painting?
The area of the frame = _____ square inches
Answer: 192 square inches
Explanation:
area of painting without frame
A1 = l × b
= 24 x 20
= 480 square inches
area of painting with frame
A2 = l × b
=28×24
=672 square inches
area of the frame not covered by paint
=area with frame(A1) – area without frame(A2)
=672 – 480
=192
Therefore the area of the frame is 192 square inches
Question 5.
One wall in Jeanne’s bedroom is 13 feet long and 8 feet tall. There is a door 3 feet wide and 6 feet tall. She has a poster on the wall that is 2 feet wide and 3 feet tall. How much of the wall is visible?
The area of the wall visible = _____ square feet
Answer: 80
Explanation:
One wall in Jeanne’s bedroom is 13 feet long and 8 feet tall.
There is a door 3 feet wide and 6 feet tall.
She has a poster on the wall that is 2 feet wide and 3 feet tall.
13 × 8 is 104. 104 – (3×6) and -(2 × 3) is 80
Thus the area of the wall visible is 80 square feet.
Common Core – Algebra: Perimeter and Area – Page No. 256
Lesson Check
Question 1.
One wall in Zoe’s bedroom is 5 feet wide and 8 feet tall. Zoe puts up a poster of her favorite athlete. The poster is 2 feet wide and 3 feet tall. How much of the wall is not covered by the poster?
Options:
a. 16 square feet
b. 34 square feet
c. 35 square feet
d. 46 square feet
Answer: 34 square feet
Explanation:
One wall in Zoe’s bedroom is 5 feet wide and 8 feet tall.
Area of the rectangle = l × w
A = 5 feet × 8 feet
A = 40 square feet
Zoe puts up a poster of her favorite athlete. The poster is 2 feet wide and 3 feet tall.
Area of the rectangle = l × w
A = 2 feet × 3 feet
S = 6 square feet
To find:
How much of the wall is not covered by the poster, we need to subtract 6 square feet from 40 square feet
40 square feet – 6 square feet = 34 square feet
Thus the are of the wall is not covered by the poster is 34 square feet.
The correct answer is option b.
Question 2.
A garage door is 15 feet wide and 6 feet high. It is painted white, except for a rectangular panel 1 foot high and 9 feet wide that is brown. How much of the garage door is white?
Options:
a. 22 square feet
b. 70 square feet
c. 80 square feet
d. 81 square feet
Answer: 81 square feet
Explanation:
Given that the garage door is 15 feet wide and 6 feet high.
W = 15 feet
H = 6 feet
Area of the rectangle = l × w
A = 6 feet × 15 feet
A = 90 square feet
It is painted white, except for a rectangular panel 1 foot high and 9 feet wide that is brown.
H = 1 foot
W = 9 feet
Area of the rectangle = l × w
A = 1 feet × 9 feet
A = 9 feet
To find:
How much of the garage door is white, we need to subtract 9 feet from 90 feet.
90 feet – 9 feet = 81 feet.
Thus the area of the garage door is white is 81 square feet.
The correct answer is option d.
Spiral Review
Question 3.
Kate baked a rectangular cake for a party. She used 42 inches of frosting around the edges of the cake. If the cake was 9 inches wide, how long was the cake?
Options:
a. 5 inches
b. 12 inches
c. 24 inches
d. 33 inches
Answer: 12 inches
Explanation:
Given,
Kate baked a rectangular cake for a party. She used 42 inches of frosting around the edges of the cake.
The width of the cake is 9 inches.
9 + 9 = 18
42 – 18 = 24
24 / 2 = 12
the length is 12 inches
Thus the correct answer is option b.
Question 4.
Larry, Mary, and Terry each had a full glass of juice. Larry drank \(\frac{3}{4}\) of his. Mary drank \(\frac{3}{8}\) of hers. Terry drank \(\frac{7}{10}\) of his. Who drank less than \(\frac{1}{2}\) of their juice?
Options:
a. Larry
b. Mary
c. Mary and Terry
d. Larry and Terry
Answer: Mary
Mary drank the least because when half of 8 is \(\frac{4}{8}\).
The correct answer is option b.
Question 5.
Which of the following statements is NOT true about the numbers 7 and 9?
Options:
a. 7 is a prime number.
b. 9 is a composite number.
c. 7 and 9 have no common factors other than 1.
d. 27 is a common multiple of 7 and 9.
Answer: 27 is a common multiple of 7 and 9.
Explanation:
Statement 27 is a common multiple of 7 and 9 is false because 27 is not the multiple of 7.
Thus the correct answer is option d.
Question 6.
Tom and some friends went to a movie. The show started at 2:30 P.M. and ended at 4:15 P.M. How long did the movie last?
Options:
a. 1 hour 35 minutes
b. 1 hour 45 minutes
c. 1 hour 55 minutes
d. 2 hours 15 minutes
Answer: 1 hour 45 minutes
Explanation:
Given,
Tom and some friends went to a movie. The show started at 2:30 P.M. and ended at 4:15 P.M.
Subtract ending time and starting time.
4 hr 15 min
-2 hr 30 min
1 hr 45 min
Thus the correct answer is option B.
Common Core – Algebra: Perimeter and Area – Page No. 257
Lesson 13.1
Find the perimeter of the rectangle or square.
Question 1.
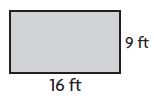
P =____ ft
Answer: 50
Explanation:
Given,
Length (L) = 16 ft
Width (W) = 9 ft
we know that the perimeter of a Rectangle is L + L+ W + W
P = L + L+ W + W
P = 16 ft + 16 ft + 9 ft + 9 ft
P = 50 ft
Therefore the perimeter of the above Rectangle is 50 ft
Question 2.
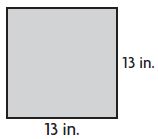
P =____ in.
Answer: 52
Explanation:
Given,
sides = 13 in.
we know that the perimeter of a square is 4×s
P = 4 × 13 in.
P = 4 × 13 in.
P = 52 in.
Therefore the perimeter of the above square is 52 in.
Question 3.
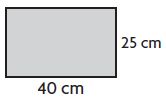
P =____ cm
Answer: 130
Explanation:
Given,
Length (L) = 40 cm
Width (W) = 25 cm
we know that the perimeter of a Rectangle is L + L+ W + W
P = L + L+ W + W
P = 40 cm + 40 cm + 25 cm + 25 cm
P = 130 cm
Therefore the perimeter of the above Rectangle is 130 cm.
Question 4.
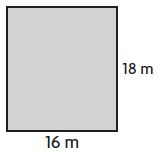
P =____ m
Answer: 68
Explanation:
Given,
Length (L) = 16 m
Width (W) = 18 m
we know that the perimeter of a Rectangle is L + L+ W + W
P = L + L+ W + W
P = 16 m+ 16 m+ 18 m+ 18 m
P = 68 m
Therefore the perimeter of the above Rectangle is 68 m.
Lesson 13.2
Find the area of the rectangle or square.
Question 5.
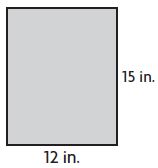
A = ____ square inches
Answer: 180
Explanation:
Given,
Height (h) = 15 in.
Breath (b) = 12 in.
Area of the rectangle = A = b×h
A = 12 in. × 15 in.
A = 180 square inches
Therefore the Area of the rectangle is 180 square inches.
Question 6.
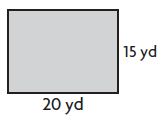
A = ____ square yards
Answer: 300
Explanation:
Given,
Height (h) = 15 yd
Breath (b) = 20 yd
Area of the rectangle = A = b×h
A = 15 yd. × 20 yd
A = 300 square yard
Therefore the Area of the rectangle is 300 square yards.
Question 7.
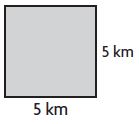
A = ____ square km
Answer: 25
Explanation:
Given,
Sides (s) = 5 km
Area of the square. A = s×s
A = 5 km × 5 km
A = 25 Square km
Therefore the Area of the square is 25 square km.
Question 8.
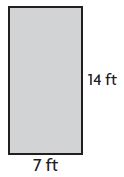
A = ____ square ft
Answer: 98
Explanation:
Given,
Height (h) = 14 ft
Breath (b) = 7 ft
Area of the rectangle = A = b×h
A = 14 ft. × 7 ft
A = 98 square ft
Therefore the Area of the rectangle is 98 square ft.
Page No: 258
Lesson 13.3
Find the area of the combined rectangles.
Question 1.
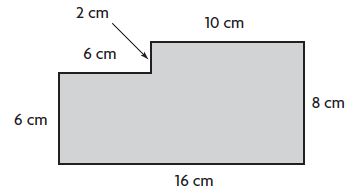
A = ____ square cm
Answer: 116 square cm
Explanation:
Divide the figure into two parts
Figure 1:
L = 6 cm
Area of the square = s × s
A = 6 cm × 6 cm = 36 sq. cm.
Figure 2:
L = 10 cm
W = 8 cm
Area of the rectangle = l × w
A = 10 cm × 8 cm = 80 sq. cm
Area of the combined rectangles = 36 sq. cm + 80 sq. cm = 116 square centimeters
Question 2.
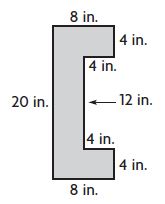
A = ____ square in.
Answer: 112 square in.
Explanation:
Divide the figure into two parts
Figure 1:
L = 8 in.
W = 4 in.
Area of the rectangle = l × w
A = 8 in. × 4 in. = 32 sq. in.
Figure 2:
L = 4 in.
W = 12 in.
Area of the rectangle = l × w
A = 4 in. × 12 in. = 48 sq. in.
Figure 3:
L = 8 in.
W = 4 in.
Area of the rectangle = l × w
A = 8 in. × 4 in. = 32 sq. in.
Area of the combined rectangles = 32 sq. in + 48 sq. in + 32 sq. in. = 112 square inches.
Lesson 13.4
Find the unknown measure of the rectangle.
Question 3.
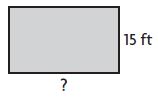
base = ____ feet
Answer: 25 feet
Explanation:
A = 375 sq. ft
h = 15 ft
Area of the rectangle = A = b×h
375 sq. ft = b × 15 ft
b = 375/15 = 25 ft
Thus the base of the figure is 25 ft.
Question 4.
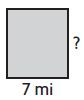
height = ____ mi
Answer: 8 mi
Explanation:
A = 56 sq. mi
b = 7 mi
Area of the rectangle = A = b×h
56 sq. mi = 7 mi × h
h = 56/7= 8 mi
Thus the height of the figure is 8 mi.
Lesson 13.5
Solve.
Question 5.
Jeanette is painting a rectangular wall that is 10 feet long and 8 feet tall. There is a window that is 5 feet wide and 3 feet tall on the wall. What is the area of the wall that Jeannette will paint?
____ square feet
Answer: 65 square feet
Explanation:
Given,
Jeanette is painting a rectangular wall that is 10 feet long and 8 feet tall.
There is a window that is 5 feet wide and 3 feet tall on the wall.
8 times 10 is eighty, then you need to subtract 3 times 5 (which is 15), and that makes it 65 feet squared.
80 sq. ft – 15 sq. ft = 65 square feet
Question 6.
Rob has a combined flower and vegetable garden that is 9 meters long and 11 meters wide. The flower garden is in the center and is a square with sides of 3 meters. How many square meters of the garden is used for vegetables?
____ square meters
Answer: 90 square meters
Explanation:
First, you would need to find the area of both the FULL veggie garden and flower garden.
Veggie Garden = 9×11 = 99
Flower Garden = 3×3 = 9
Then you would subtract the area of the veggie garden by the area of the flower garden.
99 – 9 = 90 meters squared
Conclusion:
Just solve all exercise questions and cross-check your solutions from Go Math Grade 4 Solution Key Chapter 13 Algebra Perimeter and Area. Like this, you can easily examine your strengths and weaknesses and focus on the areas you are faltering. Step-by-step Solutions presented here in the 4th Grade Go Math Answer Key Chapter Algebra Perimeter and Area useful for homework help and gain subject knowledge perfectly.
