Go Math Grade 6 Answer Key Chapter 10 Area of Parallelograms

Get Chapter 10 Area of Parallelograms Go Math Grade 6 Answer Key from this page. Here you can know the formulas of the area of a parallelogram. In order to solve the problems first, you have to know what is parallelogram and how to calculate the area of a parallelogram. Download HMH Go Math Grade 6 Solution Key Area of Parallelograms pdf here.

Go Math Grade 6 Answer Key Chapter 10 Area of Parallelograms

Check out the topics covered in Chapter 10 Area of Parallelograms before you start practicing the problems. Area of Parallelograms includes topics like the area of triangles, Area of Trapezoids, Area of Regular Polygons, Composite Figures, etc. Practice the problems a number of times and enhance your math skills. After that solve the questions given in the mid-chapter checkpoint and review test. We have also provided the solutions of mid-chapter and review test here.

Lesson 1: Algebra • Area of Parallelograms

• Share and Show – Page No. 535
• Problem Solving + Applications – Page No. 536
• Area of Parallelograms – Page No. 537
• Lesson Check – Page No. 538

Lesson 2: Investigate • Explore Area of Triangles

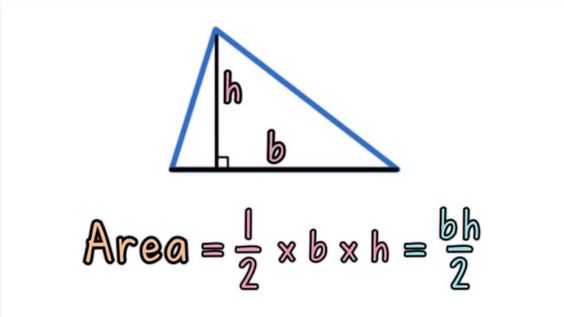
• Share and Show – Page No. 541
• Sense or Nonsense? – Page No. 542
• Explore Area of Triangles – Page No. 543
• Lesson Check – Page No. 544

Lesson 3: Algebra • Area of Triangles

• Share and Show – Page No. 547
• Unlock the Problem – Page No. 548
• Area of Triangles – Page No. 549
• Lesson Check – Page No. 550

Lesson 4: Investigate • Explore Area of Trapezoids

• Share and Show – Page No. 553
• What’s the Error? – Page No. 554
• Explore Area of Trapezoids – Page No. 555
• Lesson Check – Page No. 556

Lesson 5: Algebra • Area of Trapezoids

• Share and Show – Page No. 559
• Problem Solving + Applications – Page No. 560
• Area of Trapezoids – Page No. 561
• Lesson Check – Page No. 562

Mid-Chapter Checkpoint

• Mid-Chapter Checkpoint – Vocabulary – Page No. 563
• Mid-Chapter Checkpoint – Page No. 564

Lesson 6: Area of Regular Polygons

• Share and Show – Page No. 567
• Page No. 568
• Area of Regular Polygons – Page No. 569
• Lesson Check – Page No. 570

Lesson 7: Composite Figures

• Share and Show – Page No. 573
• Unlock the Problem – Page No. 574
• Composite Figures – Page No. 575
• Lesson Check – Page No. 576

Lesson 8: Problem Solving • Changing Dimensions

• Share and Show – Page No. 579
• On Your Own – Page No. 580
• Problem Solving Changing Dimensions – Page No. 581
• Lesson Check – Page No. 582

Lesson 9: Figures on the Coordinate Plane

• Share and Show – Page No. 585
• Problem Solving + Applications – Page No. 586
• Figures on the Coordinate Plane – Page No. 587
• Lesson Check – Page No. 588

Chapter 10 Review/Test

• Chapter 10 Review/Test – Page No. 589
• Chapter 10 Review/Test – Page No. 590
• Chapter 10 Review/Test – Page No. 591
• Chapter 10 Review/Test – Page No. 592
• Chapter 10 Review/Test – Page No. 593
• Chapter 10 Review/Test – Page No. 594

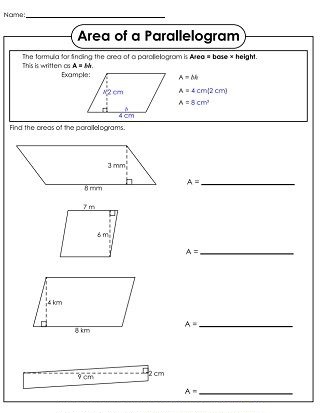
Share and Show – Page No. 535

Find the area of the parallelogram or square.

Question 1.

_______ m²

Answer: 9.96

Explanation:
Given that
Base = 8.3 m
Height = 1.2 m
We know that the area of the parallelogram is base × height
A = bh
A = 8.3 m × 1.2 m
A = 9.96 square meters
Thus the area of the parallelogram for the above figure is 9.96 m²

Question 2.

_______ ft²

Answer: 90

Explanation:
Given,
Base = 15 ft
Height = 6 ft
Area = ?
We know that,
Area of the parallelogram = bh
A = 15 ft × 6 ft
A = 90 square feet
Thus the area of the parallelogram for the above figure is 90 ft²

Question 3.

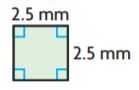
_______ mm²

Answer: 6.25

Explanation:
The above figure is a square
The side of the square is a × a
A = 2.5 mm × 2.5 mm
A = 6.25 square mm
Thus the area of the square is 6.25 mm²

Question 4.

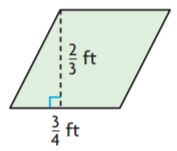
\(\frac{□}{□}\) ft²

Answer: 1/2

Explanation:
Given
Base = 3/4 ft
Height = 2/3 ft
Area of the parallelogram is base × height
A = bh
A = 3/4 × 2/3
A = 1/2
Thus the area of the above parallelogram is 1/2 ft²

Find the unknown measurement for the parallelogram.

Question 5.
Area = 11 yd²

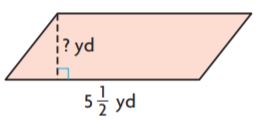
_______ yd

Answer: 2

Explanation:
Given,
A = 11 yd²
B = 5 1/2 yd
We know that
A = bh
11 = 5 1/2 × h
11 = 11/2 × h
22 = 11 × h
H = 2 yd
Thus the height of the above figure is 2 yards.

Question 6.
Area = 32 yd²

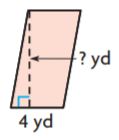
_______ yd

Answer: 8 yd

Explanation:
Given
Area = 32 yd²
Base = 4 yd
Height = ?
We know that
A = b × h
32 = 4 yd × h
H = 32/4
H = 8 yd
Therefore the height of the above figure is 8 yards.

On Your Own

Find the area of the parallelogram.

Question 7.

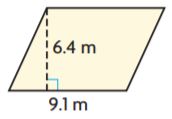
_______ m²

Answer: 58.24

Explanation:
Given
Base = 9.1 m
Height = 6.4 m
A = b × h
A = 9.1 m × 6.4 m
A = 58.24 square meters
Thus the area of the parallelogram for the above figure is 58.24 m²

Question 8.

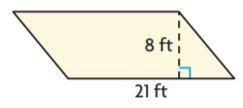
_______ ft²

Answer: 168

Explanation:
Given
Base = 21 ft
Height = 8ft
We know that the area of the parallelogram is  base × height
A = 21 ft × 8ft
A = 168 square feet
Therefore the area of the above figure is 168 ft²

Find the unknown measurement for the figure.

Question 9.
square
A = ?
s = 15 ft
A = _______ ft

Answer: 225

Explanation:
Given,
S = 15 ft
The area of the square is s × s
A = 15 ft × 15 ft
A = 225 ft²
Thus the area of the square is 225 square feet.

Question 10.
parallelogram
A = 32 m²
b = ?
h = 8 m
b = _______ m

Answer: 4

Explanation:
Given
A = 32 m²
H = 8m
B = ?
To find the base we have to use the area of parallelogram formula
A = bh
32 m² = b × 8 m
B = 32/8
B = 4 m
Thus the base is 4 meters

Question 11.
parallelogram
A = 51 \(\frac{1}{4}\) in.²
b = 8 \(\frac{1}{5}\) in.
h = ?
________ \(\frac{□}{□}\) in.

Answer: 6 \(\frac{1}{4}\) in.

Explanation:
Given,
A = 51 \(\frac{1}{4}\) in.²
b = 8 \(\frac{1}{5}\) in.
H = ?
We know that the area of the parallelogram is  base × height
A = bh
51 \(\frac{1}{4}\) = h × 8 \(\frac{1}{5}\) in.
h = 51 \(\frac{1}{4}\) ÷ 8 \(\frac{1}{5}\) in.
h = 205/4 ÷ 41/5
h = 1025/164
h = 6 \(\frac{1}{4}\) in.
Thus the height of the parallelogram is 6 \(\frac{1}{4}\) in.

Question 12.
parallelogram
A = 121 mm²
b = 11 mm
h = ?
________ mm

Answer: 11 mm

Explanation:
Given
A = 121 mm²
B = 11 mm
H = ?
We know that
A = b × h
121 mm² = 11 mm × h
H = 121/11
H = 11 mm
Thus the height is 11 mm.

Problem Solving + Applications – Page No. 536

Question 14.
Jane’s backyard is shaped like a parallelogram. The base of the parallelogram is 90 feet, and the height is 25 feet. What is the area of Jane’s backyard?

________ ft²

Answer: 2250

Explanation:
Jane’s backyard is shaped like a parallelogram.
The base of the parallelogram is 90 feet, and the height is 25 feet.
A = bh
A = 90 ft × 25 ft
A = 2250 square feet
Therefore the area of the parallelogram for the above figure is 2250 ft²

Question 15.
Jack made a parallelogram by putting together two congruent triangles and a square, like the figures shown at the right. The triangles have the same height as the square. What is the area of Jack’s parallelogram?

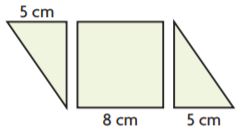
________ cm²

Answer: 104

Explanation:
Jack made a parallelogram by putting together two congruent triangles and a square, like the figures shown at the right.
The triangles have the same height as the square.
Base = 8 cm + 5 cm = 13 cm
Height = 8 cm
Area = bh
A = 13 cm × 5 cm
A = 104 square cm
Thus the area of the parallelogram is 104 cm²

Question 17.
Verify the Reasoning of Others Li Ping says that a square with 3-inch sides has a greater area than a parallelogram that is not a square but has sides that have the same length. Does Li Ping’s statement make sense? Explain.

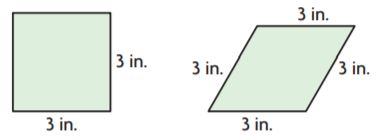
Type below:
_______________

Answer: 9

Explanation:
Base = 3 in
Height = 3 in
A = bh
A = 3 in × 3 in
A = 9 square inches
Therefore the area of the above figure is 9 in²

Question 18.
Find the area of the parallelogram.

________ in.²

Answer: 60

Explanation:
Base = 12 in
H = 5 in
A = bh
A = 12 in × 5 in
A = 60 square inches
A = 60 in²

Area of Parallelograms – Page No. 537

Find the area of the figure.

Question 1.

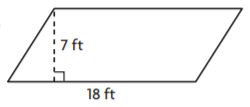
________ ft²

Answer: 126

Explanation:
The base of the figure is 18 ft
Height = 7 ft
The area of the parallelogram is bh
A = 18 ft × 7 ft
A = 126 square feet
Thus the area of the parallelogram is 126 ft²

Question 2.

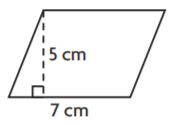
________ cm²

Answer: 35

Explanation:
Base = 7 cm
Height = 5 cm
A = bh
A = 7 cm × 5 cm
A = 35 square cm
A = 35 cm²

Find the unknown measurement for the figure.

Question 3.
parallelogram
A = 9.18 m²
b = 2.7 m
h = ?
h = ________ m

Answer: 3.4

Explanation:
A = 9.18 m²
b = 2.7 m
h = ?
A = bh
9.18 m² = 2.7 m × h
h = 9.18/2.7
A = 3.4 m

Question 4.
parallelogram
A = ?
b = 4 \(\frac{3}{10}\) m
h = 2 \(\frac{1}{10}\) m
A = ________ \(\frac{□}{□}\) m²

Explanation:
b = 4 \(\frac{3}{10}\) m
h = 2 \(\frac{1}{10}\) m
A = ?
A = bh
A = 4 \(\frac{3}{10}\) m × 2 \(\frac{1}{10}\) m
A = \(\frac{43}{10}\) m × \(\frac{21}{10}\) m
A = \(\frac{903}{100}\) m²
A = 9 \(\frac{3}{100}\) m²

Question 5.
square
A = ?
s = 35 cm
A = ________ cm²

Answer: 1225

Explanation:
s = 35 cm
A = s × s
A = 35 cm × 35 cm
A = 1225 cm²
Area of the parallelogram is 1225 cm²

Question 6.
parallelogram
A = 6.3 mm²
b = ?
h = 0.9 mm
b = ________ mm

Answer: 7

Explanation:
A = 6.3 mm²
b = ?
h = 0.9 mm
A = bh
6.3 mm² = b × 0.9 mm
b = 6.3/0.9
b = 7 mm
Thus the base of the parallelogram is 7 mm.

Problem Solving

Question 9.
Copy the two triangles and the square in Exercise 15 on page 536. Show how you found the area of each piece. Draw the parallelogram formed when the three figures are put together. Calculate its area using the formula for the area of a parallelogram.
Type below:
_______________

Answer:

First, we need to add the base of the triangle and square
So, base = 8 cm + 5 cm
base = 13 cm
The height of the triangle and square are the same.
So, h = 8 cm
Area of the parallelogram is base × height
A = bh
A = 13 cm × 5 cm
A = 104 square cm
Thus the area of the parallelogram is 104 cm²

Lesson Check – Page No. 538

Question 2.
Square County is a square-shaped county divided into 16 equal-sized square districts. If the side length of each district is 4 miles, what is the area of Square County?
________ square miles

Answer: 256 square miles

Explanation:
Square County is a square-shaped county divided into 16 equal-sized square districts.
If the side length of each district is 4 miles
4 × 4 = 16
A = 16 × 16 = 256 square miles

Spiral Review

Question 3.
Which of the following values of y make the inequality y < ^–4 true?
y = ^–4     y = ^–6      y = 0    y = ^–8    y = 2
Type below:
_______________

Answer: y = -6

Question 4.
On a winter’s day, 9°F is the highest temperature recorded. Write an inequality that represents the temperature t in degrees Fahrenheit at any time on this day.
Type below:
_______________

Answer: t ≤ 9

Explanation:
On a winter’s day, 9°F is the highest temperature recorded.
t will be less than or equal to 9.
The inequality is t ≤ 9

Question 5.
In 2 seconds, an elevator travels 40 feet. In 3 seconds, the elevator travels 60 feet. In 4 seconds, the elevator travels 80 feet. Write an equation that gives the relationship between the number of seconds x and the distance y the elevator travels.
Type below:
_______________

Answer: y = 20x

Explanation:
x represents the number of seconds
y represents the distance the elevator travels.
The elevator travels 20 feet per second.
Thus the equation is y = 20x

Question 6.
The linear equation y = 4x represents the number of bracelets y that Jolene can make in x hours. Which ordered pair lies on the graph of the equation?
Type below:
_______________

Answer: (4, 16)

Explanation:
y = 4x
If x = 4
Then y = 4(4)
y = 16
Thus the ordered pairs are (4, 16)

Share and Show – Page No. 541

Question 1.
Trace the parallelogram, and cut it into two congruent triangles. Find the areas of the parallelogram and one triangle, using square units.

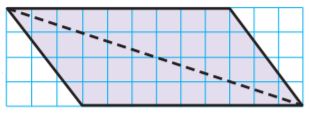
Type below:
_______________

Answer:
Base = 9 units
Height = 4 units
Area of the parallelogram = base × height
A = 9 × 4
A = 36 sq. units
Area of the triangle = ab/2
A = (9 × 4)/2
A = 18 sq. units
Area of another triangle = ab/2
A = (9 × 4)/2
A = 18 sq. units

Find the area of each triangle.

Question 2.

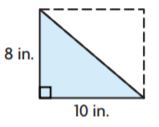
_______ in.²

Answer: 40

Explanation:
The area of the right triangle is bh/2
A = (8 × 10)/2
A = 80/2
A = 40 in.²
Thus the area of the triangle for the above figure is 40 in.²

Question 3.

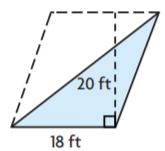
_______ ft²

Answer: 180

Explanation:
The area of the right triangle is bh/2
A = (18 × 20)/2
A = 360/2
A = 180 ft²

Question 4.

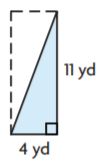
_______ yd²

Answer: 22

Explanation:
The area of the right triangle is bh/2
A = (4 × 11)/2
A = 44/2
A = 22
A = 22 yd²
Thus the area of the triangle is 22 yd²

Question 5.

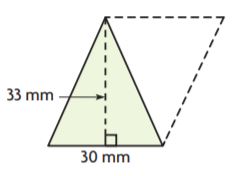
_______ mm²

Answer: 495

Explanation:
The area of the right triangle is bh/2
A = (30 × 33)/2
A = 990/2
A = 495 mm²
Thus the area of the triangle is 495 mm²

Question 6.

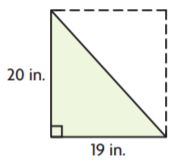
_______ in.²

Answer: 190

Explanation:
The area of the right triangle is bh/2
A = (19 × 20)/2
A = 380/2
A = 190 in.²
Thus the area of the triangle is 190 in.²

Question 7.

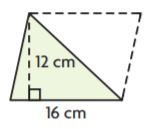
_______ cm²

Answer: 96

Explanation:
The area of the right triangle is bh/2
A = (16 × 12)/2
A = 192/2
A = 96 Sq. cm
Thus the area of the triangle is 96 Sq. cm

Problem Solving + Applications

Question 8.
Communicate Describe how you can use two triangles of the same shape and size to form a parallelogram.
Type below:
_______________

Answer: Put them together like a puzzle. if the sides are parallel then it would be a parallelogram.

Sense or Nonsense? – Page No. 542

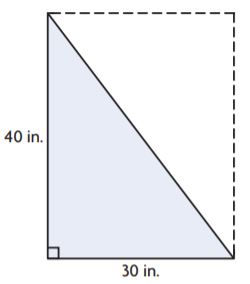
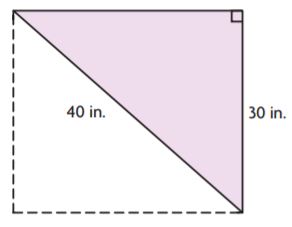
Question 10.
Cyndi and Tyson drew the models below. Each said his or her drawing represents a triangle with an area of 600 square inches. Whose statement makes sense? Whose statement is nonsense? Explain your reasoning.
Tyson’s Model:

Cyndi’s Model:

Type below:
_______________

Answer: Tyson’s Model makes sense.
The base of the figure is 30 in.
The height of the figure is 40 in
Area of the triangle = bh/2
A = (30 × 40)/2
A = 1200/2 = 600 sq. in
Cyndi’s Model doesn’t make sense because there is no base for the triangle.

Question 11.
A flag is separated into two different colors. Find the area of the white region. Show your work.

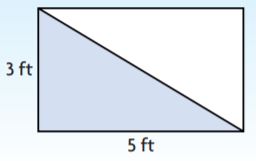
_______ ft.²

Answer: 7.5 ft.²

Explanation:
A flag is separated into two different colors.
B = 5 ft
H = 3 ft
Area of the triangle = bh/2
A = (3 × 5)/2
A = 15/2
A = 7.5 sq. ft

Explore Area of Triangles – Page No. 543

Find the area of each triangle.

Question 1.

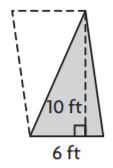
_______ ft²

Answer: 30

Explanation:
Given,
Base = 6 ft
Height = 10 ft
Area of the triangle = bh/2
A = (6 ft × 10 ft)/2
A = 60 sq. ft/2
A = 30 ft²
Thus the area of the triangle for the above figure is 0 ft²

Question 2.

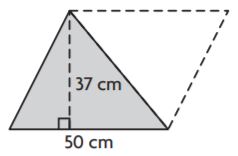
_______ cm²

Answer: 925

Explanation:
Given,
Base = 50 cm
Height = 37 cm
Area of the triangle = bh/2
A = (50 × 37)/2
A = 1850/2
A = 925 sq. cm
Therefore the area of the above figure is 925 cm²

Question 3.

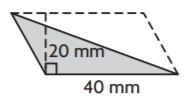
_______ mm²

Answer: 400

Explanation:
Given,
Base = 40 mm
Height = 20 mm
Area of the triangle = bh/2
A = (40 × 20)/2
A = 800/2
A = 400 mm²
Therefore the area of the above figure is 400 mm²

Question 4.

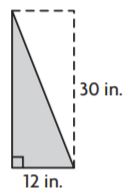
_______ in.²

Answer: 180

Explanation:
Given,
Base = 12 in.
Height = 30 in.
Area of the triangle = bh/2
A = (12 × 30)/2
A = 360/2
A = 180 in.²
Therefore the area of the above figure is 180 in.²

Question 5.

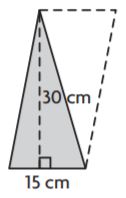
_______ cm²

Answer: 225

Explanation:
Given,
Base = 15 cm
Height = 30 cm
Area of the triangle = bh/2
A = (15 × 30)/2
A = 450/2
A = 225 cm²
Therefore the area of the above figure is 225 cm²

Question 6.

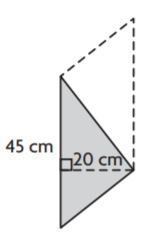
_______ cm²

Answer: 450

Explanation:
Given,
Base = 20 cm
Height = 45 cm
Area of the triangle = bh/2
A = (20 × 45)/2
A = 900/2
A = 450 cm²
Therefore the area of the above figure is 450 cm²

Problem Solving

Question 9.
Draw 3 triangles on grid paper. Draw appropriate parallelograms to support the formula for the area of the triangle. Tape your drawings to this page.
Type below:
_______________

Lesson Check – Page No. 544

Question 1.
What is the area of a triangle with a height of 14 feet and a base of 10 feet?
_______ ft²

Answer: 70

Explanation:
Given,
Base = 10 feet
Height = 14 feet
Area of the triangle = bh/2
A = (14 × 10)/2
A = 140/2
A = 70 ft²
Therefore the area of the triangle is 70 ft²

Spiral Review

Question 3.
Jack bought 3 protein bars for a total of $4.26. Which equation could be used to find the cost c in dollars of each protein bar?
Type below:
_______________

Answer: 3c = 4.26

Explanation:
Jack bought 3 protein bars for a total of $4.26.
c represents the cost of each protein bar
3c = 4.26

Question 4.
Coach Herrera is buying tennis balls for his team. He can solve the equation 4c = 92 to find how many cans c of balls he needs. How many cans does he need?
_______ cans

Answer: 23

Explanation:
Coach Herrera is buying tennis balls for his team.
4c = 92
c = 92/4
c = 23
Therefore he need 23 cans.

Question 5.
Sketch the graph of y ≤ ^–7 on a number line.
Type below:
_______________

Answer:

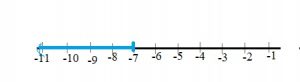
Question 6.
A square photograph has a perimeter of 20 inches. What is the area of the photograph?
_______ in.²

Answer: 25

Explanation:
A square photograph has a perimeter of 20 inches.
p = 4s
20 = 4s
s = 20/4
s = 5 in.
Area of the square is s × s
A = 5 × 5 = 25
Thus the area of square photograph = 25 in.²

Share and Show – Page No. 547

Question 1.
Find the area of the triangle.

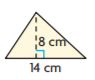
A = _______ cm²

Answer: 56

Explanation:
B = 14 cm
H = 8 cm
Area of the triangle = bh/2
A = (14 × 8)/2
A = 14 × 4
A = 56 sq. cm
Thus the area of the above figure is 56 cm²

Question 2.
The area of the triangle is 132 in.². Find the height of the triangle

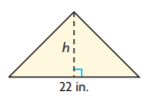
h = _______ in.

Answer: 12

Explanation:
B = 22 in.
H = ?
A = 132 in.²
Area of the triangle = bh/2
132 sq. in  = 22 in × h
h = 132 sq. in/22 in
h = 12 in
Thus the height of the above figure is 12 in.

Find the area of the triangle.

Question 3.

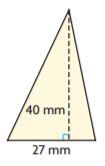
A = _______ mm²

Answer: 540

Explanation:
B = 27 mm
H = 40 mm
Area of the triangle = bh/2
A = (27 × 40)/2
A = 27 × 20 = 540
A = 540 mm²
Therefore the area of the above figure is 540 mm²

Question 4.

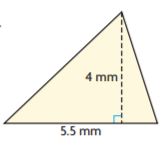
A = _______ mm²

Answer: 11

Explanation:
B = 5.5 mm
H = 4 mm
Area of the triangle = bh/2
A = (5.5 mm × 4 mm)/2
A = 5.5 mm × 2 mm
A = 11 mm²
Therefore the area of the above figure is 11 mm²

On Your Own

Find the unknown measurement for the figure.

Question 5.

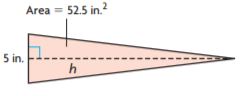
h = _______ in.

Answer: 21

Explanation:
B = 5 in
H =?
A = 52.5 sq. in
Area of the triangle = bh/2
52.5 sq. in = (5 × h)/2
52.5 sq. in × 2 = 5h
h = 21 in
Thus the height of the above figure is 21 in

Question 6.

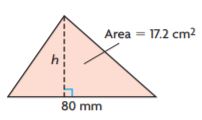
h = _______ cm

Answer: 4.3

Explanation:
B = 80 mm = 8 cm
H = ?
A = 17.2 sq. cm
Area of the triangle = bh/2
17.2 sq. cm = (8 cm × h)/2
17.2 × 2 = 8 × h
h = 4.3 cm
Thus the height of the above figure is 4.3 cm

Unlock the Problem – Page No. 548

Question 8.
Alani is building a set of 4 shelves. Each shelf will have 2 supports in the shape of right isosceles triangles. Each shelf is 14 inches deep. How many square inches of wood will she need to make all of the supports?

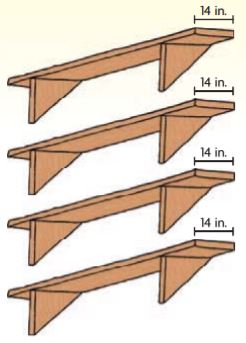
a. What are the base and height of each triangle?
Base: ___________ in.
Height: ___________ in.

Answer:
Base: 14 in
Height: 14 in

Explanation:
Given that,
Each shelf is 14 inches deep.
Height = 14 inches
By seeing the above figure we can say that the base of the shelves is 14 inches
Base = 14 inches

Question 8.
b. What formula can you use to find the area of a triangle?
Type below:
_______________

Answer: The formula to find the Area of the triangle = bh/2

Question 8.
c. Explain how you can find the area of one triangular support.
Type below:
_______________

Answer:
We can find the area of one triangle support by substituting the base and height in the formula.
A = (14 × 14)/2
A = 98 sq. in

Question 8.
d. How many triangular supports are needed to build 4 shelves?
_______ supports

Answer: 8
By seeing the above figure we can say that 8 triangular supports are needed to build 4 shelves.

Question 8.
e. How many square inches of wood will Alani need to make all the supports?
_______ in.²

Answer: 784

Explanation:
The depth of each shelf made by Alamo is 14 inches.
So the base of the right isosceles triangular supporter is 14 inches.
So one equal side is 14 cm. Now by using the Pythagoras theorem we can calculate the other side of the supporter = = 19.8 inches.
The area of the right isosceles triangle is given by × base ×height. Here the base and height are equal to 14 inches.
Therefore the area of each right isosceles triangular supporter is
A = (14 × 14)/2
A = 98 sq. in
Each shelf would require two such supporters and there are 4 such shelves. Thus the total number of supporters required is 8.
Square inches of wood necessary for 8 right isosceles triangular supporters = 98 × 8 = 784 square inches.

Question 10.
The area of a triangle is 30 ft².
For numbers, 10a–10d, select Yes or No to tell if the dimensions given could be the height and base of the triangle.
10a. h = 3, b = 10
10b. h = 3, b = 20
10c. h = 5, b = 12
10d. h = 5, b = 24
10a. ___________
10b. ___________
10c. ___________
10d. ___________

Answer:
10a. No
10b. yes
10c. Yes
10d. No

Explanation:
The area of a triangle is 30 ft².
10a. h = 3, b = 10
Area of the triangle = bh/2
A = (3 × 10)/2
A = 15 ft².
Thus the answer is no.
10b. h = 3, b = 20
Area of the triangle = bh/2
A = (3 × 20)/2
A = 30 ft².
Thus the answer is yes.
10c. h = 5, b = 12
Area of the triangle = bh/2
A = (5 × 12)/2
A = 30 ft².
Thus the answer is yes.
10d. h = 5, b = 24
Area of the triangle = bh/2
A = (5 × 24)/2
A = 60 ft².
Thus the answer is no.

Area of Triangles – Page No. 549

Find the area.

Question 1.

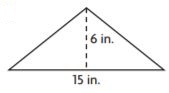
_______ in.²

Answer: 45

Explanation:
Given,
Base = 15 in.
Height = 6 in.
Area of the triangle = bh/2
A = (15 × 6)/2
A = 90/2
A = 45 in.²

Question 2.

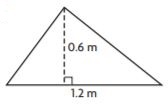
_______ m²

Answer: 0.36

Explanation:
Given,
Base = 1.2 m
Height = 0.6 m
Area of the triangle = bh/2
A = (1.2 × 0.6)/2
A = 0.72/2
A = 0.36 m²

Question 3.

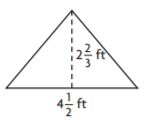
_______ ft²

Answer: 6

Explanation:
Given,
Base = 4 1/2 ft
Height = 2 2/3 ft
Area of the triangle = bh/2
A = (4 1/2 × 2 2/3)/2
A = 12/2
A = 6 ft²

Find the unknown measurement for the triangle.

Question 4.
A = 0.225 mi²
b = 0.6 mi
h = ?
h = _______ mi

Answer: 0.75

Explanation:
Given,
A = 0.225 mi²
b = 0.6 mi
h = ?
Area of the triangle = bh/2
0.225 = (0.6 × h)/2
0.450 = 0.6 × h
h = 0.450/0.6
h = 0.75 mi

Question 5.
A = 4.86 yd²
b = ?
h = 1.8 yd
b = _______ yd

Answer: 5.4 yd

Explanation:
Given,
A = 4.86 yd²
b = ?
h = 1.8 yd
Area of the triangle = bh/2
4.86 yd² = (b × 1.8 yd)/2
4.86 × 2 = b × 1.8
9.72 = b × 1.8
b = 9.72/1.8
b = 5.4 yd

Question 6.
A = 63 m²
b = ?
h = 12 m
b = _______ m

Answer: 10.5

Explanation:
Given,
A = 63 m²
b = ?
h = 12 m
Area of the triangle = bh/2
63 = (b × 12)/2
63 = b × 6
b = 63/6
b = 10.5 m

Question 7.
A = 2.5 km²
b = 5 km
h = ?
h = _______ km

Answer: 1

Explanation:
Given,
A = 2.5 km²
b = 5 km
h = ?
Area of the triangle = bh/2
2.5 = (5 km × h)/2
2.5 km² = 2.5 km × h
h = 2.5/2.5
h = 1 km

Problem Solving

Question 9.
Alicia is making a triangular sign for the school play. The area of the sign is 558 in.². The base of the triangle is 36 in. What is the height of the triangle?
_______ in.

Answer: 31

Explanation:
Given,
Alicia is making a triangular sign for the school play.
The area of the sign is 558 in.²
The base of the triangle is 36 in.
Area of the triangle = bh/2
558 = (36 × h)/2
558 = 18 × h
h = 558/18
h = 31 inches

Question 10.
Describe how you would find how much grass seed is needed to cover a triangular plot of land.
Type below:
_______________

Answer:

You will need to find the area
A=height multiplied by the base divided by 2
Area of the triangle = bh/2

Lesson Check – Page No. 550

Spiral Review

Question 3.
Tina bought a t-shirt and sandals. The total cost was $41.50. The t-shirt cost $8.95. The equation 8.95 + c = 41.50 can be used to find the cost c in dollars of the sandals. How much did the sandals cost?
$ _______

Answer: $32.55

Explanation:
Tina bought a t-shirt and sandals.
The total cost was $41.50.
The t-shirt cost $8.95.
8.95 + c = 41.50
c = 41.50 – 8.95
c = $32.55

Question 4.
There are 37 paper clips in a box. Carmen places more paper clips in the box. Write an equation to show the total number of paper clips p in the box after Carmen places n more paper clips in the box.
Type below:
_______________

Answer: 37 + n = p

Explanation:
There are 37 paper clips in a box. Carmen places more paper clips in the box.
n represents number of paper clips in the box
The equation is 37 + n = p

Question 5.
Name another ordered pair that is on the graph of the equation represented by the table.

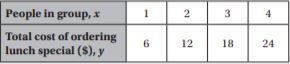
Type below:
_______________

Answer: The ordered pairs are (1, 6), (2, 12), (3, 18), (4, 16)

Question 6.
Find the area of the triangle that divides the parallelogram in half.

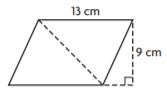
_______ cm²

Answer: 58.5

Explanation:
Given,
b = 13 cm
h = 9 cm
Area of the triangle = bh/2
A = (13 × 9)/2
A = 117/2
A = 58.5 cm²

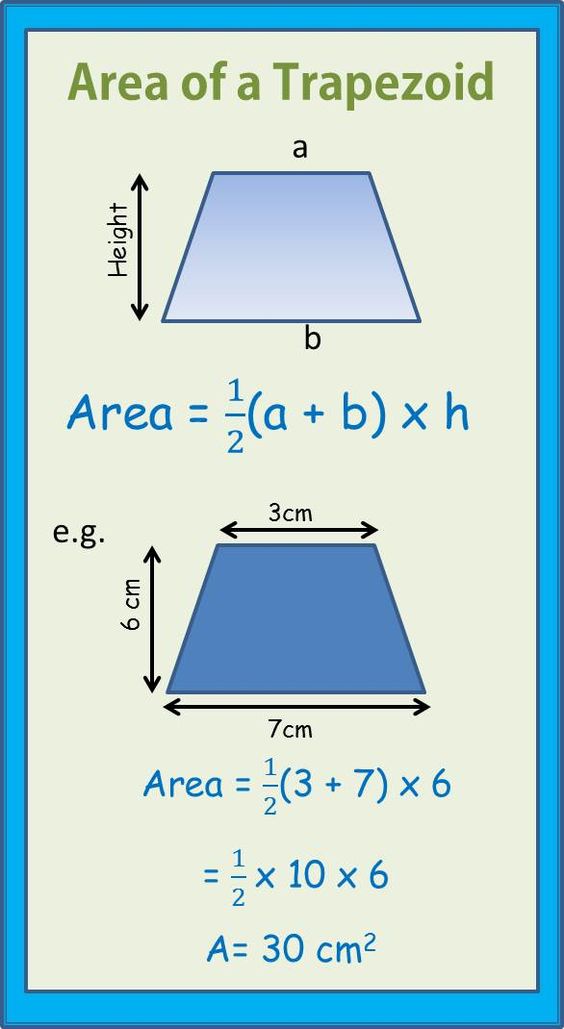
Share and Show – Page No. 553

Question 1.
Trace and cut out two copies of the trapezoid. Arrange the trapezoids to form a parallelogram. Find the areas of the parallelogram and one trapezoid using square units

Type below:
_______________

Answer:
Figure 1:
Base 1 = 3 units
Base 2= 7 units
Height = 4 units
Area of the trapezium = (b1 + b2)h/2
A = (3 + 7)4/2
A = 10 × 2
A = 20 sq. units
Figure 2:
Base 1 = 7 units
Base 2= 3 units
Height = 4 units
Area of the trapezium = (b1 + b2)h/2
A = (7 + 3)4/2
A = 10 × 2
A = 20 sq. units

Find the area of the trapezoid.

Question 2.

_______ cm²

Answer: 40

Explanation:
Base 1 = 6 cm
Base 2 = 10 cm
Height = 5 cm
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
A = (6 cm + 10 cm)5 /2
A = (16 × 5)/2
A = 40 sq. cm

Question 3.

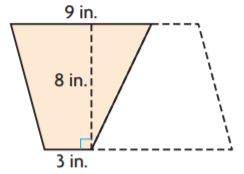
_______ in.²

Answer: 48

Explanation:
b1 = 3 in
b2 = 9 in.
h = 8 in.
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
A = (3 + 9)8/2
A = 12 × 4
A = 48 sq. in

Question 4.

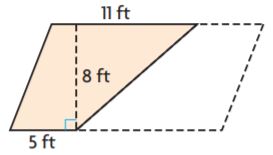
_______ ft²

Answer: 64

Explanation:
b1 = 11 ft
b2 = 5 ft
h = 8 ft
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
A = (11 + 5)8/2
A = 16 × 4
A = 64 sq. ft

Question 5.

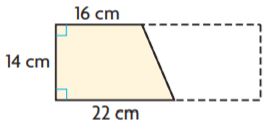
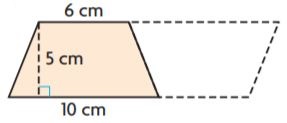
_______ cm²

Answer: 266

Explanation:
b1 = 16 cm
b2 = 22 cm
h = 14 cm
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
A = (16 + 22)14/2
A = 38 × 7
A = 266 sq. cm

Question 6.

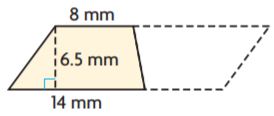
_______ mm²

Answer: 71.5

Explanation:
b1 = 8 mm
b2 = 14 mm
h = 6.5 mm
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
A = (8 + 14)6.5/2
A = 11 × 6.5
A = 71.5 sq. mm

Question 7.

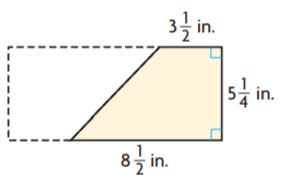
_______ in.²

Answer: 31.5

Explanation:
b1 = 3 1/2 in.
b2 = 8 1/2 in.
h = 5 1/4 in.
We know that the Area of the trapezium is the sum of bases into height divided by 2.
Area of the trapezium = (b1 + b2)h/2
b = 3 1/2 + 8 1/2
b = 12
A = 5 1/4 × 12/2
A = 5 1/4 × 6
A = 31.5 sq. in

Problem Solving + Applications

Question 8.
Describe a Method Explain one way to find the height of a trapezoid if you know the area of the trapezoid and the length of both bases.
Type below:
_______________

Answer:
1) Add the length of both bases: [Total Length = Length 1 + Length 2]
2) Divide the length that you found by 2. [Average Length = Total Length ÷ 2]
3) Divide the Area by the length found [Height = Area ÷ average length]

What’s the Error? – Page No. 554

Question 10.
Except for a small region near its southeast corner, the state of Nevada is shaped like a trapezoid. The map at the right shows the approximate dimensions of the trapezoid. Sabrina used the map to estimate the area of Nevada.
Look at how Sabrina solved the problem. Find her error.
Two copies of the trapezoid can be put together to form a rectangle.
length of rectangle: 200 + 480 = 680 mi
width of rectangle: 300 mi
A = lw
A = 680 × 300
A = 204,000
The area of Nevada is about 204,000 square miles.
Describe the error. Find the area of the trapezoid to estimate the area of Nevada.
Type below:
_______________

Answer:
The area of Nevada is she didn’t divide by 2.
Area of the trapezium = (b1 + b2)h/2
A = (200 + 480)300/2
A = 680 × 150
A = 102000 sq. miles

Question 11.
A photo was cut in half at an angle. What is the area of one of the cut pieces?

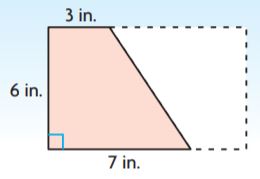
_______ in.²

Answer: 30

Explanation:
b1= 3 in
b2 = 7 in
h = 6 in.
Area of the trapezium = (b1 + b2)h/2
A = (3 + 7)6/2
A = 10 × 3
A = 30 sq. in
Thus the area of the trapezium is 30 in.²

Explore Area of Trapezoids – Page No. 555

Question 1.
Trace and cut out two copies of the trapezoid. Arrange the trapezoids to form a parallelogram. Find the areas of the parallelogram and the trapezoids using square units.

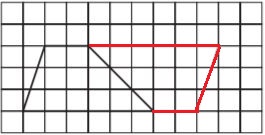
Type below:
_______________

Answer:
Figure 1:
b1 = 2 units
b2 = 6 units
h = 3 units
Area of the trapezium = (b1 + b2)h/2
A = (2 + 6)3/2
A = (8)(3)/2
A = 24/2 = 12
A = 12 sq. units
Figure 2:
b1 = 6 units
b2 = 2 units
h = 3 units
Area of the trapezium = (b1 + b2)h/2
A = (6 + 2)3/2
A = (8)(3)/2
A = 24/2 = 12
The area of figure 2 is 12 sq. units

Find the area of the trapezoid.

Question 2.

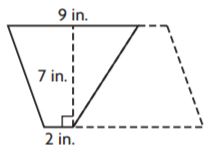
_______ in.²

Answer: 38.5

Explanation:
Given,
b1 = 9 in
b2 = 2 in
h = 7 in
Area of the trapezium = (b1 + b2)h/2
A = (9 + 2)7/2
A = (11 × 7)/2
A = 77/2 = 38.5 in.²

Question 3.

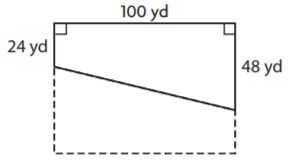
_______ yd²

Answer: 3600

Explanation:
Given,
b1 = 24 yd
b2 = 48 yd
h = 100 yd
Area of the trapezium = (b1 + b2)h/2
A = (24 + 48)100/2
A = 72 × 50
A = 3600 yd²

Question 4.

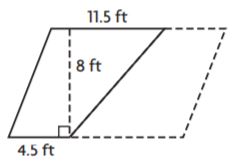
_______ ft²

Answer: 64

Explanation:
Given,
b1 = 4.5 ft
b2 = 11.5 ft
h = 8 ft
Area of the trapezium = (b1 + b2)h/2
A = (4.5 + 11.5)8/2
A = 16 × 4
A = 64 sq. ft

Problem Solving

Question 5.
A cake is made out of two identical trapezoids. Each trapezoid has a height of 11 inches and bases of 9 inches and 14 inches. What is the area of one of the trapezoid pieces?
_______ in.²

Answer: 126.5

Explanation:
Given,
A cake is made out of two identical trapezoids.
Each trapezoid has a height of 11 inches and bases of 9 inches and 14 inches.
Area of the trapezium = (b1 + b2)h/2
A = (9 + 14)11/2
A = 23 × 11/2
A = 126.5 in.²

Question 7.
Find the area of a trapezoid that has bases that are 15 inches and 20 inches and a height of 9 inches.
_______ in.²

Answer: 157.5

Explanation:
b1 = 15 inches
b2 = 20 inches
h = 9 inches
Area of the trapezium = (b1 + b2)h/2
A = (15 + 20)9/2
A = (35 × 9)/2
A = 157.5 sq. in

Lesson Check – Page No. 556

Question 8.

_______ yd²

Answer: 84

Explanation:
b1 = 9 yd
b2 = 15 yd
h = 7 yd
Area of the trapezium = (b1 + b2)h/2
A = (9 + 15)7/2
A = 24 × 3.5
A = 84 sq. yd

Question 2.
Maggie colors a figure in the shape of a trapezoid. The trapezoid is 6 inches tall. The bases are 4.5 inches and 8 inches. What is the area of the figure that Maggie colored?
_______ in.²

Answer: 37.5

Explanation:
Maggie colors a figure in the shape of a trapezoid.
The trapezoid is 6 inches tall.
The bases are 4.5 inches and 8 inches.
b1 = 4.5 in
b2 = 8 in
h = 6 in
Area of the trapezium = (b1 + b2)h/2
A = (4.5 in + 8 in)6/2
A = 12.5 in × 3
A = 37.5 sq. in

Spiral Review

Question 4.
Ginger makes pies and sells them for $14 each. Write an equation that represents the situation, if y represents the money that Ginger earns and x represents the number of pies sold.
Type below:
_______________

Answer: y = 14x

Explanation:
Ginger makes pies and sells them for $14 each.
y represents the money that Ginger earns
x represents the number of pies sold
The equation is y = 14x

Question 5.
What is the equation for the graph shown below?

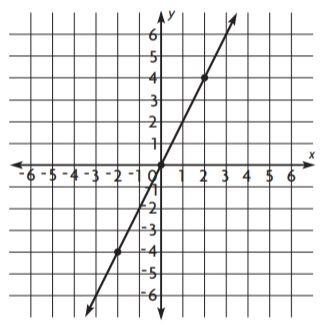
Type below:
_______________

Answer: y = 2x
By seeing the graph we can say that y = 2x

Question 6.
Cesar made a rectangular banner that is 4 feet by 3 feet. He wants to make a triangular banner with the same area as the other. The triangular banner will have a base of 4 feet. What should its height be?
_______ feet

Answer: 6

Explanation:
6 Because 4×3=12 and (4× 6)/2=12

Share and Show – Page No. 559

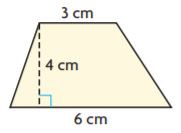
Question 1.
Find the area of the trapezoid.

A = _______ cm²

Answer: 18

Explanation:
Given,
b1 = 6 cm
b2 = 3 cm
h = 4 cm
We know that,
Area of the trapezium = (b1 + b2)h/2
A = (6 cm + 3 cm)4 cm/2
A = 9 cm × 2 cm
A = 18 sq. cm
Therefore the area of the trapezoid is 18 cm²

Question 2.
The area of the trapezoid is 45 ft². Find the height of the trapezoid.

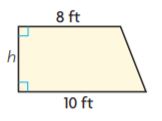
h = _______ ft

Answer: 5

Explanation:
b1 = 10 ft
b2 = 8 ft
The area of the trapezoid is 45 ft²
We know that,
Area of the trapezium = (b1 + b2)h/2
45 ft² = (10 ft + 8 ft)h/2
90 = 18 × h
h = 90/18
h = 5 ft
Thus the height of the above figure is 5 ft.

Question 3.
Find the area of the trapezoid.

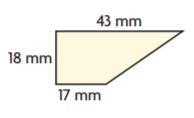
_______ mm²

Answer: 540

Explanation:
b1 = 17 mm
b2 = 43 mm
h = 18 mm
We know that,
Area of the trapezium = (b1 + b2)h/2
A = (17 + 43)18/2
A = 60 mm × 9 mm
A = 540 sq. mm
Thus the area of the trapezoid is 540 mm²

On Your Own

Find the area of the trapezoid.

Question 4.

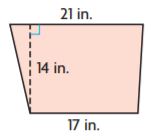
A = _______ in.²

Answer: 266

Explanation:
Given,
b1 = 17 in
b2 = 21 in
h = 14 in
We know that,
Area of the trapezium = (b1 + b2)h/2
A = (17 in + 21 in)14/2
A = 38 in × 7 in
A = 266 sq. in
Therefore Area of the trapezium is 266 in.²

Question 5.

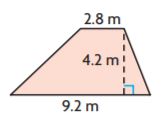
A = _______ m²

Answer: 25.2 m²

Explanation:
Given,
b1 = 9.2 m
b2 = 2.8 m
h = 4.2 m
We know that,
Area of the trapezium = (b1 + b2)h/2
A = (9.2 + 2.8)4.2/2
A = 12 × 2.1
A = 25.2 sq. m
Therefore the area of the trapezium is 25.2 m²

Find the height of the trapezoid.

Question 6.

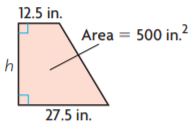
h = _______ in.

Answer: 25

Explanation:
Given,
b1 = 27.5 in
b2 = 12.5 in
h = ?
A = 500 sq. in
We know that,
Area of the trapezium = (b1 + b2)h/2
500 sq. in = (27.5 in + 12.5 in)h/2
500 sq. in = 40 × h/2
500 sq. in = 20h
h = 500/20
h = 25 inches
Thus the height of the above figure is 25 inches.

Question 7.

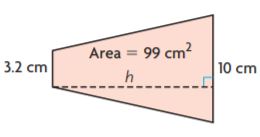
h = _______ cm

Answer: 15

Explanation:
A = 99 sq. cm
b1 = 3.2 cm
b2 = 10 cm
h = ?
We know that,
Area of the trapezium = (b1 + b2)h/2
99 sq. cm = (3.2 cm+ 10 cm)h/2
99 sq. cm = (13.2 cm)h/2
99 sq. cm = 6.6 × h
h = 99 sq. cm/6.6 cm
h = 15 cm

Problem Solving + Applications – Page No. 560

Use the diagram for 8–9.

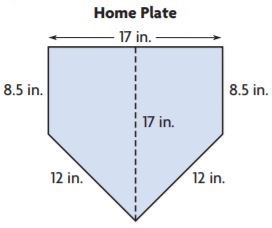
Question 8.
A baseball home plate can be divided into two trapezoids with the dimensions shown in the drawing. Find the area of home plate.
_______ in.²

Answer: 21.75

Explanation:
The bases of the trapezoid area are 8.5 in and 17 in and the height is 8.5 in.
We know that,
Area of the trapezium = (b1 + b2)h/2
A = 1/2 (8.5 + 17)8.5
A = (25.5)(8.5)/2
A = 1/2 × 216.75
The area of the home plate is double the area of a trapezoid.
So, the area of the home plate is 216.75 sq. in.

Question 9.
Suppose you cut the home plate along the dotted line and rearranged the pieces to form a rectangle. What would the dimensions and the area of the rectangle be?
Type below:
_______________

Answer:
The dimensions of the rectangle would be 25.5 in by 8.5 in.
The area would be 216.75 sq. in.

Question 10.
A pattern used for tile floors is shown. A side of the inner square measures 10 cm, and a side of the outer square measures 30 cm. What is the area of one of the yellow trapezoid tiles?

_______ cm²

Answer: 200 sq. cm

Explanation:
A side of the inner square measures 10 cm, and a side of the outer square measures 30 cm.
The bases of the trapezoid are 10 cm and 30 cm and the height of the trapezoid is 10 cm.
We know that,
Area of the trapezium = (b1 + b2)h/2
A = (10 + 30)10/2
A = 40 cm × 5 cm
A = 200 sq. cm
So, the area of one of the yellow trapezoid tiles is 200 sq. cm

Question 12.
Which expression can be used to find the area of the trapezoid? Mark all that apply.

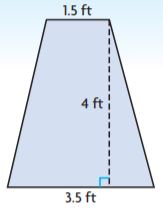
Options:
a. \(\frac{1}{2}\) × (4 + 1.5) × 3.5
b. \(\frac{1}{2}\) × (1.5 + 3.5) × 4
c. \(\frac{1}{2}\) × (4 + 3.5) × 1.5
d. \(\frac{1}{2}\) × (5) × 4

Answer: \(\frac{1}{2}\) × (1.5 + 3.5) × 4

Explanation:
b1 = 3.5 ft
b2 = 1.5 ft
h = 4 ft
We know that,
Area of the trapezium = (b1 + b2)h/2
A = (3.5 ft + 1.5 ft)4ft/2
A = \(\frac{1}{2}\) × (1.5 + 3.5) × 4
Thus the correct answer is option B.

Area of Trapezoids – Page No. 561

Find the area of the trapezoid.

Question 1.

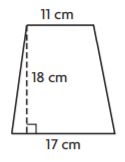
_______ cm²

Answer: 252 cm²

Explanation:
Given that,
long base b1 = 17 cm
short base b2 = 11 cm
h = 18 cm
We know that,
The Area of the trapezium = (b1 + b2)h/2
A = (17 cm + 11 cm)18 cm/2
A = 28 cm × 9 cm
A = 252 cm²
Thus the area of the trapezium for the above figure is 252 cm²

Question 2.

_______ ft²

Answer: 30 ft²

Explanation:
Given,
b1 = 6.5 ft
b2 = 5.5 ft
h = 5 ft
We know that,
The Area of the trapezium = (b1 + b2)h/2
A = (6.5 + 5.5)5/2
A = 12 ft × 2.5 ft
A = 30 sq. ft
Therefore the area of the trapezium is 30 ft²

Question 3.

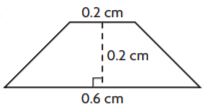
_______ cm²

Answer: 0.08 cm²

Explanation:
Given,
b1 = 0.6 cm
b2 = 0.2 cm
h = 0.2 cm
We know that,
The Area of the trapezium = (b1 + b2)h/2
A = (0.6 cm + 0.2 cm)0.2 cm/2
A = 0.8 cm × 0.1 cm
A = 0.08 sq. cm
Thus the area of the trapezium is 0.08 sq. cm

Question 4.

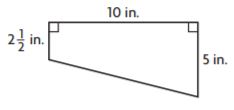
_______ in.²

Answer: 37.5 in.²

Explanation:
Given,
b1 = 5 in
b2 = 2 1/2
h = 10 in
We know that,
The Area of the trapezium = (b1 + b2)h/2
A = (5 in + 2 1/2 in)10/2
A = 7 1/2 × 5
A = 37.5 sq. in
Thus the area of the trapezium is 37.5 in.²

Problem Solving

Question 5.
Sonia makes a wooden frame around a square picture. The frame is made of 4 congruent trapezoids. The shorter base is 9 in., the longer base is 12 in., and the height is 1.5 in. What is the area of the picture frame?
_______ in.²

Answer: 63

Explanation:
Given,
Sonia makes a wooden frame around a square picture.
The frame is made of 4 congruent trapezoids.
The shorter base is 9 in., the longer base is 12 in., and the height is 1.5 in.
We know that,
The Area of the trapezium = (b1 + b2)h/2
A = (9 in + 12 in)1.5/2
A = 21 in × 1.5 in/2
A = 63 sq. in
Thus the area of the trapezium is 63 in.²

Question 6.
Bryan cuts a piece of cardboard in the shape of a trapezoid. The area of the cutout is 43.5 square centimeters. If the bases are 6 centimeters and 8.5 centimeters long, what is the height of the trapezoid?
_______ cm

Answer: 6 cm

Explanation:
Given,
Bryan cuts a piece of cardboard in the shape of a trapezoid.
The area of the cutout is 43.5 square centimeters.
If the bases are 6 centimeters and 8.5 centimeters long.
We know that,
The Area of the trapezium = (b1 + b2)h/2
43.5 sq. cm = (6 + 8.5)h/2
43.5 × 2 = 14.5 × h
h = 6 cm
Therefore the height of the trapezoid is 6 cm.

Lesson Check – Page No. 562

Question 1.
Dominic is building a bench with a seat in the shape of a trapezoid. One base is 5 feet. The other base is 4 feet. The perpendicular distance between the bases is 2.5 feet. What is the area of the seat?
_______ ft²

Answer: 11.25 sq. ft

Explanation:
Given,
Dominic is building a bench with a seat in the shape of a trapezoid.
One base is 5 feet. The other base is 4 feet.
The perpendicular distance between the bases is 2.5 feet.
We know that,
The Area of the trapezium = (b1 + b2)h/2
A = (5 ft + 4 ft)2.5/2
A = 4.5 ft × 2.5 ft
A = 11.25 sq. ft
Thus the area of the seat is 11.25 sq. ft

Question 2.
Molly is making a sign in the shape of a trapezoid. One base is 18 inches and the other is 30 inches. How high must she make the sign so its area is 504 square inches?
_______ in.

Answer: 21 in.

Explanation:
Given,
Molly is making a sign in the shape of a trapezoid.
One base is 18 inches and the other is 30 inches.
A = 504 sq. in
We know that,
The Area of the trapezium = (b1 + b2)h/2
504 sq. in = (18 + 30)h/2
504 sq. in = 24 × h
h = 504 sq. in÷ 24 in
h = 21 inches
Thus the height of the trapezoid is 21 inches.

Spiral Review

Question 3.
Write these numbers in order from least to greatest.
3 \(\frac{3}{10}\)     3.1       3 \(\frac{1}{4}\)
Type below:
_______________

Explanation:
First, convert the fraction into a decimal.
3 \(\frac{3}{10}\) = 3.3
3 \(\frac{1}{4}\) = 3.25
Now write the numbers from least to greatest.
3.1 3.25 3.3

Question 4.
Write these lengths in order from least to greatest.
2 yards       5.5 feet        70 inches
Type below:
_______________

Answer: 5.5 feet, 70 inches, 2 yards

Explanation:
First, convert from inches to feet.
1 feet = 12 inches
70 inches = 5.8 ft
1 yard = 3 feet
2 yards = 2 × 3 ft
2 yards = 6 feet
Now write the numbers from least to greatest.
5.5 ft 5.8 ft 6 ft

Question 6.
Brian frosted a cake top shaped like a parallelogram with a base of 13 inches and a height of 9 inches. Nancy frosted a triangular cake top with a base of 15 inches and a height of 12 inches. Which cake’s top had the greater area? How much greater was it?
Type below:
_______________

Explanation:
Parallelogram Formula = Base × Height
A=bh
A=13 × 9=117 in
Triangle Formula=
A=1/2bh
A=1/2 × 15 × 12 = 90 in
Brian’s cake top has a greater area, and by 27 inches.

Mid-Chapter Checkpoint – Vocabulary – Page No. 563

Choose the best term from the box to complete the sentence.

Question 1.
A _____ is a quadrilateral that always has two pairs of parallel sides.
Type below:
_______________

Answer: A parallelogram is a quadrilateral that always has two pairs of parallel sides.

Question 2.
The measure of the number of unit squares needed to cover a surface without any gaps or overlaps is called the _____.
Type below:
_______________

Answer: The measure of the number of unit squares needed to cover a surface without any gaps or overlaps is called the Area.

Question 3.
Figures with the same size and shape are _____.
Type below:
_______________

Answer: Figures with the same size and shape are Congruent.

Concepts and Skills

Find the area.

Question 4.

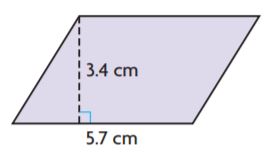
_______ cm²

Answer: 19.38

Explanation:
b = 5.7 cm
h = 3.4 cm
Area of parallelogram = bh
A = 5.7 cm × 3.4 cm
A = 19.38 cm²
Thus the area of the parallelogram is 19.38 cm²

Question 5.

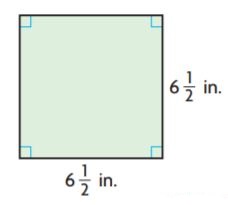
_______ \(\frac{□}{□}\) in.²

Answer: 42 \(\frac{1}{4}\) in.²

Explanation:
b = 6 \(\frac{1}{2}\)
h = 6 \(\frac{1}{2}\)
Area of parallelogram = bh
A = 6 \(\frac{1}{2}\) × 6 \(\frac{1}{2}\)
A = 42 \(\frac{1}{4}\) in.²
Thus the area of the parallelogram is 42 \(\frac{1}{4}\) in.²

Question 6.

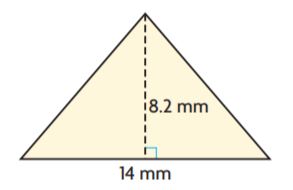
_______ mm²

Answer: 57.4

Explanation:
b = 14 mm
h = 8.2 mm
A = bh/2
A = (14 mm × 8.2 mm)/2
A = 57.4 mm²

Question 7.

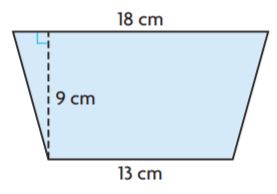
Answer: 139.5

Explanation:
b1 = 13 cm
b2= 18 cm
h = 9 cm
Area of the trapezium = (b1 + b2)h/2
A = (13 + 18)9/2
A = 31 × 4.5
A = 139.5 sq. cm

Page No. 564

Question 10.
The height of a parallelogram is 3 times the base. The base measures 4.5 cm. What is the area of the parallelogram?
_______ cm²

Answer: 60.75

Explanation:
The height of a parallelogram is 3 times the base. The base measures 4.5 cm.
A = bh
h = 3 × 4.5
h = 13.5 cm
b = 4.5 cm
A = 13.5 cm × 4.5 cm
A = 60.75 cm²

Question 11.
A triangular window pane has a base of 30 inches and a height of 24 inches. What is the area of the window pane?
_______ in.²

Answer: 360

Explanation:
A triangular window pane has a base of 30 inches and a height of 24 inches.
b = 30 in
h = 24 in
A = bh/2
A = (30 × 24)/2
A = 30 × 12
A = 360 in.²

Question 12.
The courtyard behind Jennie’s house is shaped like a trapezoid. The bases measure 8 meters and 11 meters. The height of the trapezoid is 12 meters. What is the area of the courtyard?
_______ m²

Answer: 114

Explanation:
Given,
The courtyard behind Jennie’s house is shaped like a trapezoid.
The bases measure 8 meters and 11 meters.
The height of the trapezoid is 12 meters.
Area of the trapezium = (b1 + b2)h/2
A = (8 + 11)12/2
A = 19 × 6
A = 114 m²

Question 13.
Rugs sell for $8 per square foot. Beth bought a 9-foot-long rectangular rug for $432. How wide was the rug?
_______ feet

Answer: 6 feet

Explanation:
If you know the rugs sell for 8$ per square foot and the total spend was $432.
You divide 432 by 8 to find the total number of square feet of the rug.
To find the total square foot you find the area.
So the area of a rectangle is L × W. So 54 = 9 × width.
So just divide 54 by 9 and you get the width of the rug.
The width is 6 feet.
Now you check. A nine by 6 rug square foot is 54. and then times by 8 and you get 432 total.

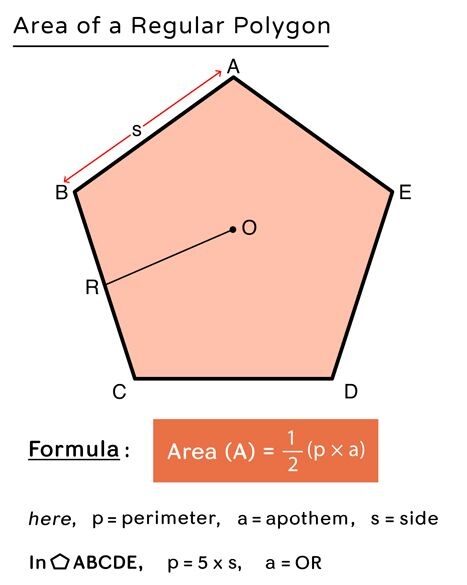
Share and Show – Page No. 567

Find the area of the regular polygon.

Question 1.

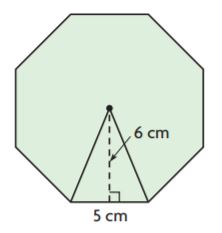
_______ cm²

Answer: 120

Explanation:
b = 5 cm
h = 6 cm
Number of congruent figures inside the figure: 8
Area of each triangle = bh/2
A = (5 cm)(6 cm)/2
A = 15 sq. cm
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of regular octagon = 8 × 15 sq. cm
A = 120 sq. cm
Therefore the area of the regular octagon for the above figure = 120 sq. cm

Question 2.

_______ m²

Answer: 60

Explanation:
Given,
b = 6 m
h = 4 m
Number of congruent figures inside the figure: 5
Area of each triangle = bh/2
A = (6 m)(4 m)/2
A = 12 sq. m
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
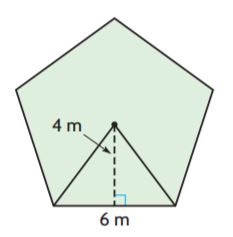
Area of regular pentagon = 5 × 12 sq. m
A = 60 sq. m
Therefore the area of the above figure is 60 sq. m.

Question 3.

_______ mm²

Answer: 480

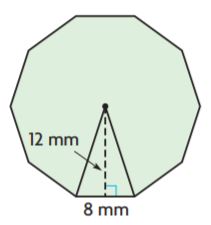
Explanation:
Given,
b = 8 mm
h = 12 mm
Number of congruent figures inside the figure: 10
Area of each triangle = bh/2
A = (12 mm)(8 mm)/2
A = 48 sq. mm
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of regular polygon = 10 × 48 sq. mm
A = 480 sq. mm
Therefore, the area of the regular polygon is 480 sq. mm

On Your Own

Find the area of the regular polygon.

Question 4.

_______ cm²

Answer: 168

Explanation:
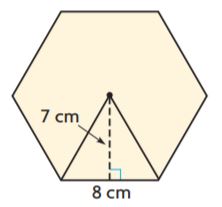
Given,
b = 8 cm
h = 7 cm
Number of congruent figures inside the figure: 6
Area of each triangle = bh/2
A = (8 cm)(7 cm)/2
A = 28 sq. cm
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of regular hexagon = 6 × 28 sq. cm
A = 168 sq. cm
Thus the area of the above figure is 168 sq. cm

Question 5.

_______ in.²

Answer: 6020

Explanation:
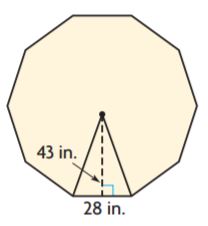
Given,
b = 28 in
h = 43 in
Number of congruent figures inside the figure: 10
Area of each triangle = bh/2
A = (28 in)(43 in)/2
A = 602 sq. in
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of regular polygon = 10 × Area of each triangle
A = 10 × 602 sq. in
A = 6020 sq. in
Therefore the area of the regular polygon is 6020 sq. in

Question 6.
Explain A regular pentagon is divided into congruent triangles by drawing a line segment from each vertex to the center. Each triangle has an area of 24 cm². Explain how to find the area of the pentagon
Type below:
_______________

Answer: 120

Explanation:
Given,
Each triangle has an area of 24 cm².
Pentagon has 5 sides. The number of congruent figures is 5.
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of regular pentagon = 5 × 24 sq. cm
A = 120 sq. cm
Therefore the area of the pentagon is 120 sq. cm

Page No. 568

Question 7.
Name the polygon and find its area. Show your work.

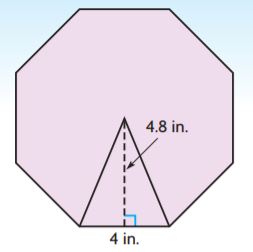
_______ in.²

Answer: 76.8 sq. in

Explanation:
b = 4 in
h = 4.8 in
Number of configured figures of the regular polygon: 8
Area of the triangle = bh/2
A = (4)(4.8)/2
A = 9.6 sq. in.
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of regular polygon = 8 × area of the triangle
A = 8 × 9.6 sq. in.
A = 76.8 sq. in
Thus the area of the regular polygon is 76.8 sq. in.

Regular polygons are common in nature

One of the bestknown examples of regular polygons in nature is the small hexagonal cells in honeycombs constructed by honeybees. The cells are where bee larvae grow. Honeybees store honey and pollen in the hexagonal cells. Scientists can measure the health of a bee population by the size of the cells.

Question 8.
Cells in a honeycomb vary in width. To find the average width of a cell, scientists measure the combined width of 10 cells, and then divide by 10.
The figure shows a typical 10-cell line of worker bee cells. What is the width of each cell?

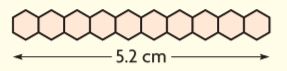
_______ cm

Answer: 0.52 cm

Explanation:
Since the combined width of 10 cells is 5.2 cm, the width of each cell is 5.2 ÷ 10 = 0.52 cm.

Question 9.
The diagram shows one honeycomb cell. Use your answer to Exercise 8 to find h, the height of the triangle. Then find the area of the hexagonal cell.

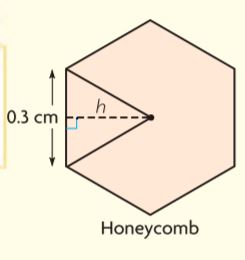
Type below:
_______________

Answer: 0.234 sq. cm

Explanation:
The length of the h, the height of the triangle, is half of the width of each cell.
Since the width of each cell is 0.52 cm
h = 0.52 ÷ 2 = 0.26 cm
Area of the triangle = bh/2
A = (0.3)(0.26)/2
A = 0.078/2
A = 0.039
The area of the hexagon is:
6 × 0.039 = 0.234 sq. cm.

Area of Regular Polygons – Page No. 569

Find the area of the regular polygon.

Question 1.

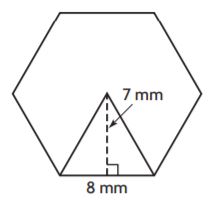
_______ mm²

Answer: 168

Explanation:
Given,
b = 8 mm
h = 7 mm
Number of congruent figures inside the figure: 6
Area of each triangle = bh/2
A = (8)(7)/2
A = 28 sq. mm
Now to find the area of regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of regular polygon = 6 × 28 sq. mm
A = 168 sq. mm
Therefore the area of the regular polygon for the above figure is 168 sq. mm

Question 2.

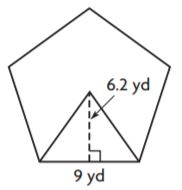
_______ yd²

Answer: 139.5

Explanation:
Given,
b = 9 yd
h = 6.2 yd
Number of congruent figures inside the figure: 5
Area of each triangle = bh/2
A = (9 yd) (6.2 yd)/2
A = 9 yd × 3.1 yd
A = 27.9 sq. yd
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of regular polygon = 5 × 27.9 sq. yd
A = 139.5 sq. yd
Thus the area of the regular polygon for the above figure is 139.5 sq. yd.

Question 3.

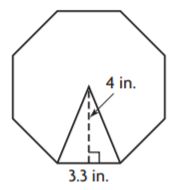
_______ in.²

Answer: 52.8

Explanation:
Given,
b = 3.3 in
h = 4 in
Number of congruent figures inside the figure: 8
Area of each triangle = bh/2
A = (3.3 in)(4 in)/2
A = 6.6 sq. in
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of regular polygon = 8 × 6.6 sq. in
A = 52.8 sq. in
The area of the regular polygon is 52.8 sq. in

Problem Solving

Question 4.
Stu is making a stained glass window in the shape of a regular pentagon. The pentagon can be divided into congruent triangles, each with a base of 8.7 inches and a height of 6 inches. What is the area of the window?
_______ in.²

Answer: 130.5

Explanation:
Stu is making a stained glass window in the shape of a regular pentagon.
The pentagon can be divided into congruent triangles, each with a base of 8.7 inches and a height of 6 inches.
Number of congruent figures inside the figure: 5
Area of each triangle = bh/2
A = (8.7 in)(6 in)/2
A = 8.7 in × 3 in
A = 26.1 sq. in.
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of regular polygon = 5 × 26.1 sq. in
A = 130.5 sq. in
Thus the area of the window is 130.5 sq. in

Question 6.
A square has sides that measure 6 inches. Explain how to use the method in this lesson to find the area of the square.
Type below:
_______________

Answer: 36 sq. in

Explanation:
A square has sides that measure 6 inches.
s = 6 in
We know that,
Area of the square = s × s
A = 6 in × 6 in
A = 36 sq. in
Thus the area of the square is 36 sq. in

Lesson Check – Page No. 570

Question 1.
What is the area of the regular hexagon?

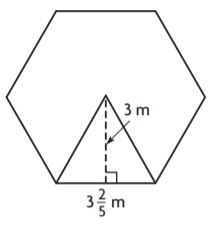
________ \(\frac{□}{□}\) m²

Answer: 30 \(\frac{3}{5}\) m²

Explanation:
Given,
b = 3 \(\frac{2}{5}\) m
h = 3 m
Area of each triangle = bh/2
A = 3 \(\frac{2}{5}\) m × 3/2 m
A = 5.1 sq. m
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of the regular hexagon = 6 × 5.1 = 30.6
= 30 \(\frac{6}{10}\) m²
= 30 \(\frac{3}{5}\) m²
Therefore the area of the regular hexagon is 30 \(\frac{3}{5}\) m²

Question 2.
A regular 7-sided figure is divided into 7 congruent triangles, each with a base of 12 inches and a height of 12.5 inches. What is the area of the 7-sided figure?
________ in.²

Answer: 525 sq. in

Explanation:
A regular 7-sided figure is divided into 7 congruent triangles, each with a base of 12 inches and a height of 12.5 inches.
Area of each triangle = bh/2
A = (12 in)(12.5 in)/2
A = 12.5 in × 6 in
A = 75 sq. inches
Thus the area of each triangle = 75 sq. in
Now to find the area of the regular polygon we have to multiply the area of each triangle and number of congruent figures.
Area of regular polygon = 7 × 75 sq. in
A = 525 sq. in
Thus the area of the 7-sided figure is 525 sq. in

Spiral Review

Question 3.
Which inequalities have b = 4 as one of its solutions?
2 + b ≥ 2      3b ≤ 14
8 − b ≤ 15     b − 3 ≥ 5
Type below:
_______________

Answer: b − 3 ≥ 5

Explanation:
Substitute b = 4 in the inequality
i. 2 + b ≥ 2
2 + 4 ≥ 2
6 ≥ 2
ii. 3b ≤ 14
3(4) ≤ 14
12 ≤ 14
iii. 8 − b ≤ 15
8 – 4 ≤ 15
4 ≤ 15
iv. b − 3 ≥ 5
4 – 3 ≥ 5
1 ≥ 5
1 is not greater than or equal to 5.

Question 5.
What is the area of triangle ABC?

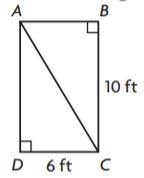
________ ft²

Answer: 30 ft²

Explanation:
b = 6 ft
h = 10 ft
We know that,
Area of each triangle = bh/2
A = (6 ft)(10 ft)/2
A = 60 sq. ft/2
A = 30 sq. ft
Therefore the area of triangle ABC is 30 sq. ft

Question 6.
Marcia cut a trapezoid out of a large piece of felt. The trapezoid has a height of 9 cm and bases of 6 cm and 11 cm. What is the area of Marcia’s felt trapezoid?
________ cm²

Answer: 76.5 cm²

Explanation:
Marcia cut a trapezoid out of a large piece of felt.
The trapezoid has a height of 9 cm and bases of 6 cm and 11 cm.
Area of the trapezium = (b1 + b2)h/2
A = (6 + 11)9/2
A = 17 cm × 4.5 cm
A = 76.5 sq. cm
Therefore the area of Marcia’s felt trapezoid is 76.5 cm²

Share and Show – Page No. 573

Question 1.
Find the area of the figure.

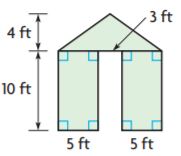
________ ft²

Answer: 126 sq. ft

Explanation:
Figure 1:
l = 10 ft
w = 5 ft
A = lw
A = 10 ft × 5 ft
A = 50 sq. ft
Figure 2:
l = 10 ft
w = 5 ft
A = lw
A = 10 ft × 5 ft
A = 50 sq. ft
Figure 3:
b = 5 ft + 5 ft + 3 ft
b = 13 ft
h = 4 ft
Area of triangle = bh/2
A = 13 ft × 4 ft/2
A = 13 ft × 2 ft
A = 26 sq. ft
Add the areas of all the figures = 50 sq. ft + 50 sq. ft + 26 sq. ft
Thus the Area of the composite figure is 126 sq. ft.

Find the area of the figure.

Question 2.

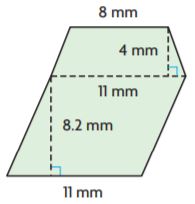
________ mm²

Answer: 128.2 sq. mm

Explanation:
Figure 1:
b1 = 11 mm
b2 = 11 mm
h = 8.2 mm
Area of the trapezoid = (b1 + b2)h/2
A = (11 mm + 11 mm)8.2 mm/2
A = 22 mm × 4.1 mm
A = 90.2 sq. mm
Figure 2:
b1 = 11mm
b2 = 8mm
h = 4mm
Area of the trapezoid = (b1 + b2)h/2
A = (11mm + 8mm)4mm/2
A = 19mm × 2mm
A = 38 sq. mm
Add the areas of both figures = 90.2 sq. mm + 38 sq. mm
Thus the area of the figure is 128.2 sq. mm

Question 3.

________ m²

Answer: 144 sq. m

Explanation:
Figure 1:
l = 12 m
w = 7 m
Area of Rectangle = lw
A = 12m × 7m
A = 84 sq. m
Figure 2:
Area of right triangle = ab/2
a = 5m
b = 12m
A = (5m)(12m)/2
A = 30 sq. m
Figure 3:
Area of right triangle = ab/2
a = 5m
b = 12m
A = (5m)(12m)/2
A = 30 sq. m
Area of all figures = 84 sq. m + 30 sq. m + 30 sq. m = 144 sq. m.
Therefore the area of the figure is 144 sq. m

On Your Own

Question 4.
Find the area of the figure.

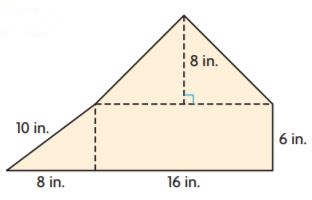
________ in.²

Answer: 184 sq. in

Explanation:
Figure 1:
b = 8 in
h = 6 in
Area of right triangle = ab/2
A = 8 in × 6 in/2
A = 24 sq. in
Figure 2:
Area of Rectangle = lw
A = 16 in × 6 in
A = 96 sq. in
Figure 3:
Area of right triangle = ab/2
b = 8 in
h = 8 in
A = 8 in × 8 in/2
A = 32 sq. in
Figure 4:
Area of right triangle = ab/2
b = 8 in
h = 8 in
A = 8 in × 8 in/2
A = 32 sq. in
Area of all figures = 24 sq. in + 96 sq. in + 32 sq. in + 32 sq. in = 184 sq. in
Thus the area of the figure = 184 sq. in.

Question 5.
Attend to Precision Find the area of the shaded region.

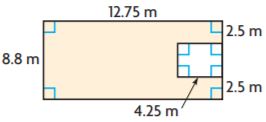
________ m²

Answer: 96.05 sq. m

Explanation:
Figure 1:
Area of Rectangle = lw
A = 12.75 m × 8.8 m
A = 112.2 sq. m
Figure 2:
Area of Rectangle = lw
l = 4.25 m
w = 3.3 m
A = 4.25 m × 3.3 m
A = 16.15 sq. m
Area of all the figures = 112.2 sq. m + 16.15 sq. m = 90.05 sq. m
Therefore the area of the figure = 90.05 sq. m

Unlock the Problem – Page No. 574

Question 6.
Marco made the banner shown at the right. What is the area of the yellow shape?

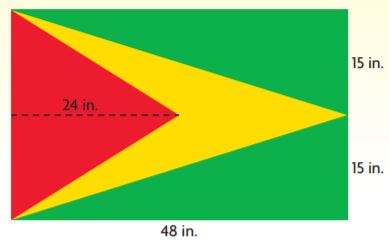
a. Explain how you could find the area of the yellow shape if you knew the areas of the green and red shapes and the area of the entire banner.
Type below:
_______________

Answer: I can find the area of the yellow shape by subtracting the areas of the green and red shapes from the area of the entire banner.

Question 6.
b. What is the area of the entire banner? Could you explain how you found it?
The area of the banner is ________ in.²

Answer: 1440 sq. in

Explanation:
The banner is a rectangle with a width of 48 inches and a length of 30 inches.
A = lw
A = 48 in × 30 in
A = 1440 sq. in
Therefore, the area of the banner is 1440 sq. in.

Question 6.
c. What is the area of the red shape? What is the area of each green shape?
The area of the red shape is ________ in.²
The area of each green shape is ________ in.²

Answer:
The area of the red shape is 360 in.²
The area of each green shape is 360 in.²

Explanation:
The red shape is a triangle with a base of 30 inches and a height of 24 inches.
A = bh/2
A = (30)(24)/2
A = 360 sq. in.
The area of the red triangle is 360 sq. in.
Each green shape is a triangle with a base of 15 inches and a height of 48 inches.
A = bh/2
A = 1/2 × 15 × 48
A = 720/2
A = 360 sq. in
Therefore the area of each green triangle is 360 sq. in.

Question 6.
d. What equation can you write to find A, the area of the yellow shape?
Type below:
_______________

Answer: A = 1440 – (360 + 360 + 360)

Question 6.
e. What is the area of the yellow shape?
The area of the yellow shape is ________ in.²

Answer: 360 sq. in

Explanation:
A = bh/2
A = 1/2 × 15 × 48
A = 720/2
A = 360 sq. in
Therefore the area of the yellow shape is 360 sq. in

Question 8.
Sabrina wants to replace the carpet in a few rooms of her house. Select the expression she can use to find the total area of the floor that will be covered. Mark all that apply.

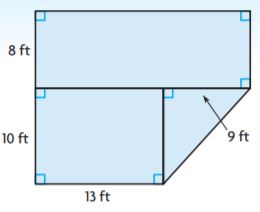
Options:
a. 8 × 22 + 130 + \(\frac{1}{2}\) × 10 × 9
b. 18 × 22 − \(\frac{1}{2}\) × 10 × 9
c. 18 × 13 + \(\frac{1}{2}\) × 10 × 9
d. \(\frac{1}{2}\) × (18 + 8) × 22

Answer: 8 × 22 + 130 + \(\frac{1}{2}\) × 10 × 9

Explanation:
Figure 1:
l = 13 ft
w = 10 ft
Area of the rectangle = lw
A = 13 ft × 10 ft = 130
Figure 2:
b = 9 ft
h = 10 ft
Area of the triangle = bh/2
A = (9)(10)/2
A = 45 sq. ft
Figure 3:
Area of the rectangle = lw
l = 22 ft
w = 8 ft
The area of the composite figure is 8 × 22 + 130 + \(\frac{1}{2}\) × 10 × 9
Thus the correct answer is option A.

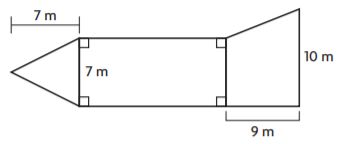
Composite Figures – Page No. 575

Find the area of the figure

Question 1.

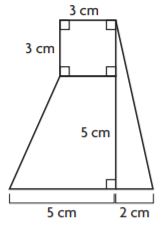
________ cm²

Answer: 37 cm²

Explanation:
Area of square = s × s
A = 3 × 3 = 9 sq. cm
Area of Triangle = bh/2
A = 2 × 8/2 = 8 sq. cm
Area of the trapezoid = (b1 + b2)h/2
A = (5 + 3)5/2
A = 4 × 5 = 20 sq. in
Area of composite figure = 9 sq. cm + 8 sq. cm + 20 sq. in
A = 37 cm²

Question 2.

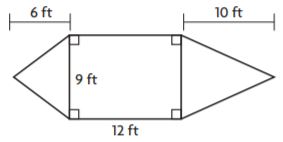
________ ft²

Answer:

Explanation:
Figure 1:
b = 9 ft
h = 6 ft
Area of Triangle = bh/2
A = (9ft)(6ft)/2
A = 27 sq. ft
Figure 2:
l = 12 ft
w = 9 ft
Area of the rectangle = lw
A = (12ft)(9ft)/2
A = 12 ft × 9 ft
A = 108 sq. ft
Figure 3:
Area of Triangle = bh/2
b = 9 ft
h = 10 ft
A = (10ft)(9ft)/2
A = 45 sq. ft
Area of the composite figure = 27 sq. ft + 108 sq. ft + 45 sq. ft = 180 sq. ft

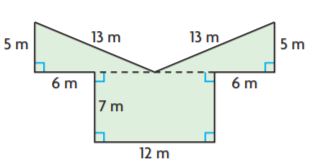
Question 3.

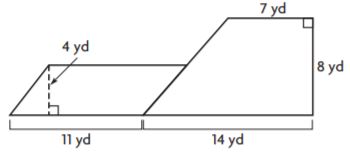
________ yd²

Answer: 128 yd²

Explanation:
Figure 1:
b1 = 7 yd
b2 = 14 yd
h = 8 yd
Area of the trapezoid = (b1 + b2)h/2
A = (7yd + 14yd)8yd/2
A = 21 yd × 4 yd
A = 84 sq. yd
Figure 2:
b = 11 yd
h = 4 yd
Area of the parallelogram = bh
A = 11yd × 4yd = 44 sq. yd
Area of the composite figure = 84 sq. yd + 44 sq. yd = 128 sq. yd

Problem Solving

Question 4.
Janelle is making a poster. She cuts a triangle out of poster board. What is the area of the poster board that she has left?

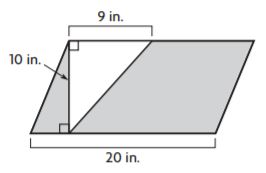
________ in.²

Answer: 155 sq. in

Explanation:
The poster is a parallelogram, and it’s area is:
A = bh
A = 20 x 10
A = 200 sq. in
The area of the triangle that Janelle cut out of the poster board is:
A = 1/2bh
A = 1/2 x 10 x 9
A = 90/2
A = 45 sq. in
The area of the poster board that she has left is 200 sq. in – 45 sq. in = 155 sq. in

Question 5.
Michael wants to place grass on the sides of his lap pool. Find the area of the shaded regions that he wants to cover with grass.

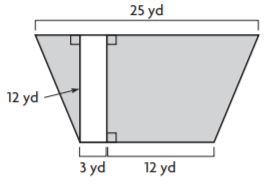
________ yd²

Answer: 204 yd²

Explanation:
The area of the shaded region can be found by finding the total area and subtracting the area of the lap pool.
Total area = Area of the trapezium = 1/2 × (Sum of parallel sides) × distance between them
Sum of parallel sides = 25 yd + (3 + 12) = 40 yd
Distance between them = 12 yd
Total area = 1/2 × 40 × 12 = 240 yd²
Find the area of the lap pool.
Area = length × width = 12 × 3 = 36 yd²
Find the area of the shaded region
Area to be covered with grass = 240 – 36 = 204 yd²

Question 6.
Describe one or more situations in which you need to subtract to find the area of a composite figure.
Type below:
_______________

Answer:

Figure 1:
Area of Rectangle = lw
A = 12.75 m × 8.8 m
A = 112.2 sq. m
Figure 2:
Area of Rectangle = lw
l = 4.25 m
w = 3.3 m
A = 4.25 m × 3.3 m
A = 16.15 sq. m
Area of all the figures = 112.2 sq. m + 16.15 sq. m = 90.05 sq. m
Therefore the area of the figure = 90.05 sq. m

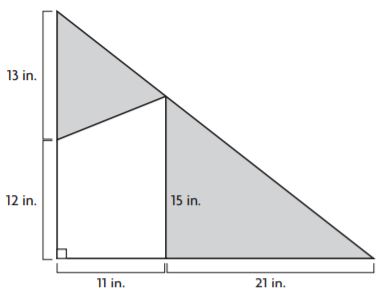
Lesson Check – Page No. 576

Question 1.
What is the area of the composite figure?

________ m²

Answer: 227 m²

Explanation:
Figure 1:
b = 7 m
h = 7 m
Area of the triangle = bh/2
A = (7m)(7m)/2
A = 24.5 sq. m
Figure 2:
b1 = 7m
b2 = 10m
h = 9m
Area of the trapezoid = (b1 + b2)h/2
A = (7m + 10m)9m/2
A = 17m × 4.5 m
A = 76.5 sq. m
Area of the rectangle = lw
A = 18m × 7m
A = 126 sq. m
Area of the figures = 24.5 sq. m + 76.5 sq. m + 126 sq. m = 227 sq. m
Thus the area of the figure is 227 sq. m

Question 2.
What is the area of the shaded region?

________ in.²

Answer: 251.5 in.²

Explanation:
Figure 1:
l = 21 in
w = 15 in
Area of triangle = bh/2
A = 21 in × 15 in/2
A = 157.5 sq. in
Figure 2:
b1 = 12 in
b2 = 15 in
h = 11 in
Area of the trapezoid = (b1 + b2)h/2
A = (12 in + 15 in)11 in/2
A = 27 in × 5.5 in
A = 148.5 sq. in
Figure 3:
b = 13 in
h = 14.4 in
Area of trinagle = bh/2
A = 13 × 14.4in/2
A = 13in × 7.2 in
A = 94 sq. in
The area of the shaded region is 94 sq. in + 157.5 sq. in = 251.5 in.²

Spiral Review

Question 3.
In Maritza’s family, everyone’s height is greater than 60 inches. Write an inequality that represents the height h, in inches, of any member of Maritza’s family.
Type below:
_______________

Answer: h > 60

Explanation:
Given, Maritza’s family, everyone’s height is greater than 60 inches.
The inequality is h > 60

Question 4.
The linear equation y = 2x represents the cost y for x pounds of apples. Which ordered pair lies on the graph of the equation?
Type below:
_______________

Answer: (2, 4)

Explanation:
y = 2x
put x = 2
y = 2(2)
y = 4
The ordered pair is (2,4)

Question 6.
A regular hexagon has sides measuring 7 inches. If the hexagon is divided into 6 congruent triangles, each has a height of about 6 inches. What is the approximate area of the hexagon?
________ in.²

Answer: 126 in.²

Explanation:
b = 7 in
h = 6 in
Number of congruent figures: 6
Area of the triangle = bh/2
A = (7in)(6in)/2
A = 21 sq. in
Area of regular hexagon = 6 × area of each triangle
A = 6 × 21 sq. in
A = 126 sq. in
Thus the approximate area of the hexagon is 126 sq. in.

Share and Show – Page No. 579

Question 1.
The dimensions of a 2-cm by 6-cm rectangle are multiplied by 5. How is the area of the rectangle affected?
Type below:
_______________

Answer: 25

Explanation:
The dimensions of a 2-cm by 6-cm rectangle are multiplied by 5.
Original Area:
Area of rectangle = lw
A = 2cm × 6cm = 12 sq. cm
New dimensions:
l = 6 × 5 = 30 cm
w = 2 × 5 = 10 cm
The new area is:
A = 10 cm × 30 cm = 300 sq. cm
New Area/ Original Area = 300/12 = 25
So, the new area is 25 times the original area.

Question 3.
Evan bought two square rugs. The larger one measured 12 ft square. The smaller one had an area equal to \(\frac{1}{4}\) the area of the larger one. What fraction of the side lengths of the larger rug were the side lengths of the smaller one?
Type below:
_______________

Answer:
Since the area of the smaller rug is \(\frac{1}{4}\) times the area of the larger rug, the side lengths of the smaller rug are \(\frac{1}{2}\) of the side lengths of the larger one.

Question 4.
On Silver Island, a palm tree, a giant rock, and a buried treasure form a triangle with a base of 100 yd and a height of 50 yd. On a map of the island, the three landmarks form a triangle with a base of 2 ft and a height of 1 ft. How many times the area of the triangle on the map is the area of the actual triangle?

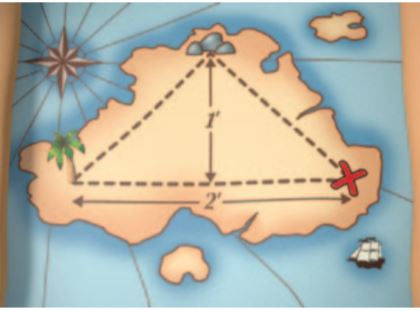
Type below:
_______________

Answer: 45,000

Explanation:
Area of triangle= (1/2) (base x height)
1 yard = 3 foot
Base of the actual triangle= 100 yards= 300ft
Height of the actual triangle= 50 yards= 150ft.
Area of the actual triangle= (1/2) (300 x 150) = 45000 square ft
The base of the triangle on the map = 2ft
Height of the triangle on the map= 1ft
Area of the triangle on the map= (1/2) (2 x 1) = 1 square ft.
The actual area is 45000 time the area of the map

On Your Own – Page No. 580

Question 5.
A square game board is divided into smaller squares, each with sides one-ninth the length of the sides of the board. Into how many squares is the game board divided?
________ small squares

Answer: 81 small squares

Explanation:
Each side of the game board is divided into 9 lengths.
The game board is divided into 9 × 9 = 81 small squares.
Thus, the board is divided into 81 small squares.

Question 6.
Flynn County is a rectangle measuring 9 mi by 12 mi. Gibson County is a rectangle with an area 6 times the area of Flynn County and a width of 16 mi. What is the length of Gibson County?
________ mi

Answer: 40.5 mi.

Explanation:
Flynn County is a rectangle measuring 9 mi by 12 mi.
Gibson County is a rectangle with an area 6 times the area of Flynn County and a width of 16 mi.
The area of Flynn Country is
A = 9 × 12 = 108 sq. mi
The area of Gibson Country is
A = 6 × 108 = 648 sq. mi
A = lw
648 = 16 × l
l = 648/16
l = 40.5 mi
Therefore the length of Gibson Country is 40.5 miles.

Question 7.
Use Diagrams Carmen left her house and drove 10 mi north, 15 mi east, 13 mi south, 11 mi west, and 3 mi north. How far was she from home?
________ miles

Answer:
15 mi – 11 mi = 4 miles
Thus Carmen is 4 miles from home.

Question 8.
Bernie drove from his house to his cousin’s house in 6 hours at an average rate of 52 mi per hr. He drove home at an average rate of 60 mi per hr. How long did it take him to drive home?
________ hours

Answer: 5.2 hours

Explanation:
Given,
Bernie drove from his house to his cousin’s house in 6 hours at an average rate of 52 mi per hr. He drove home at an average rate of 60 mi per hr.
The distance from Bernie’s house to his cousin’s house is
52 mi/hr × 6hr = 52 × 6mi = 312 miles
On the way back, he drove for
312mi ÷ 60mi/hr = 5.2 hours
Therefore it takes 5.2 hours for Bernie to drive home.

Problem Solving Changing Dimensions – Page No. 581

Read each problem and solve.

Question 1.
The dimensions of a 5-in. by 3-in. rectangle are multiplied by 6. How is the area affected?
Type below:
_______________

Answer: 36

Explanation:
Original area: A = 5 × 3 = 15 sq. in
new dimensions:
l = 6 × 5 = 30 in
w = 6 × 3 = 18 in
New Area = l × w
A = 30 in × 18 in
A = 540 sq. in
Thus new area = 540 sq. in
new area/original area = 540/15 = 36
Thus the area was multiplied by 36.

Question 3.
The dimensions of a 3-ft by 6-ft rectangle are multiplied by \(\frac{1}{3}\). How is the area affected?
Type below:
_______________

Answer: 1/9

Explanation:
Original area: A = 3 ft × 6 ft = 18 sq. ft
new dimensions:
l = 3 ft × \(\frac{1}{3}\) = 1 ft
w = 6 ft × \(\frac{1}{3}\) = 2 ft
New area: A = 1 ft × 2 ft = 2 sq. ft
new area/original area = 2/18 = 1/9
The area was multiplied by 1/9.

Question 4.
The dimensions of a triangle with base 10 in. and height 4.8 in. are multiplied by 4. How is the area affected?
Type below:
_______________

Answer: 16

Explanation:
original area: A = 10 in × 4.8 in = 48 sq. in
new dimensions:
l = 10 in × 4 = 40 in
w = 4.8 in × 4 = 19.2 in
new area = l × w
A = 40 in × 19.2 in
A = 768 sq. in
new area/original area = 768/48
Thus the area was multiplied by 16.

Question 5.
The dimensions of a 1-yd by 9-yd rectangle are multiplied by 5. How is the area affected?
Type below:
_______________

Answer: 25

Explanation:
original area: A = 1 yd × 9 yd = 9 sq. yd
new dimensions:
l = 1 yd × 5 = 5 yd
w = 9 yd × 5 = 45 yd
new area = 5 yd × 45 yd = 225 sq. yd
new area/original area = 225 sq. yd/9 sq. yd
Thus the area was multiplied by 25.

Question 7.
The dimensions of a triangle are multiplied by \(\frac{1}{4}\). The area of the smaller triangle can be found by multiplying the area of the original triangle by what number?
Type below:
_______________

Answer: 1/16

Explanation:
We can find the area of the original triangle by multiplying with \(\frac{1}{4}\)
\(\frac{1}{4}\) × \(\frac{1}{4}\) = \(\frac{1}{16}\)
Thus the area was multiplied by \(\frac{1}{16}\)

Question 8.
Write and solve a word problem that involves changing the dimensions of a figure and finding its area.
Type below:
_______________

Answer:
The dimensions of a triangle with a base 1.5 m and height 6 m are multiplied by 2. How is the area affected?
Original area:
Area of triangle = bh/2
A = (1.5m)(6m)/2
A = 4.5 sq. m
new dimensions:
b = 1.5m × 2 = 3 m
h = 6 m × 2 = 12 m
Area of triangle = bh/2
A = (12m × 3m)/2
A = 6m × 3m
A = 18 sq. m
new area/original area = 18 sq. m/4.5 sq. m
The area was multiplied by 4.

Lesson Check – Page No. 582

Question 1.
The dimensions of Rectangle A are 6 times the dimensions of Rectangle B. How do the areas of the rectangles compare?
Type below:
_______________

Answer: Area of Rectangle A = 36 × Area of Rectangle B

Explanation:
The area of Rectangle A will always be 36 times the area of Rectangle B.
If Rectangle B has length 1 and width 2, Rectangle A will have length 6 and width 12. By multiplying, Rectangle A will have an area of 72 and B 2. Divide the two numbers and you will have 36.

Question 2.
A model of a triangular piece of jewelry has an area that is \(\frac{1}{4}\) the area of the jewelry. How do the dimensions of the triangles compare?
Type below:
_______________

Answer: Model dimensions = 1/2 jewelry dimensions

Explanation:
The dimensions of the model area
1/4 ÷ 2 = 1/2 times the dimensions of the piece of jewelry.

Spiral Review

Question 4.
Graph y > 3 on a number line.
Type below:
_______________

Answer:

Question 5.
The parallelogram below is made from two congruent trapezoids. What is the area of the shaded trapezoid?

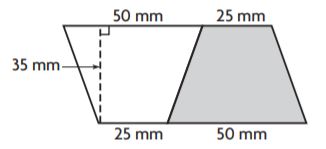
________ mm²

Answer: 1312.5 sq. mm

Explanation:
Given,
b1 = 25mm
b2 = 50mm
h = 35mm
Area of the trapezoid = (b1 + b2)h/2
A = (25mm + 50mm)35mm/2
A = 75mm × 35mm/2
A = 1312.5 sq. mm
Thus the area of the shaded region is 1312.5 sq. mm

Question 6.
A rectangle has a length of 24 inches and a width of 36 inches. A square with side length 5 inches is cut from the middle and removed. What is the area of the figure that remains?
________ in.²

Answer: 839 sq. in

Explanation:
Area of rectangle = lw
A = 24 in × 36 in
A = 864 sq. in
Area of square = s × s
s = 5 in
A = 5 in × 5 in
A = 25 sq. in
Area of the figure that remains = 864 sq. in – 25 sq. in
A = 839 sq. in

Share and Show – Page No. 585

Question 1.
The vertices of triangle ABC are A(−1, 3), B(−4, −2), and C(2, −2). Graph the triangle and find the length of side \(\overline { BC } \).
________ units

Answer: 6 units

Give the coordinates of the unknown vertex of rectangle JKLM, and graph.

Question 2.

Type below:
_______________

Answer:

Question 3.

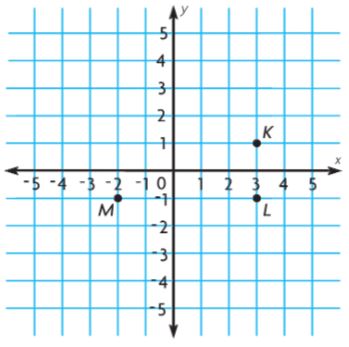
Type below:
_______________

Answer:

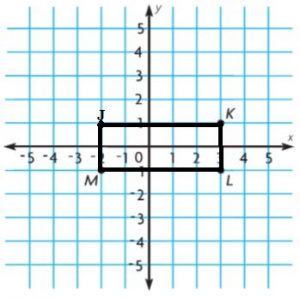
On Your Own

Question 4.
Give the coordinates of the unknown vertex of rectangle PQRS, and graph.

Type below:
_______________

Answer:

Question 5.
The vertices of pentagon PQRST are P(9, 7), Q(9, 3), R(3, 3), S(3, 7), and T(6, 9). Graph the pentagon and find the length of side \(\overline { PQ } \).
________ units

Answer: 4 units

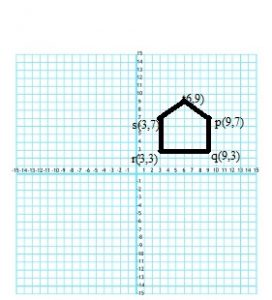
Problem Solving + Applications – Page No. 586

The map shows the location of some city landmarks. Use the map for 6–7.

Question 6.
A city planner wants to locate a park where two new roads meet. One of the new roads will go to the mall and be parallel to Lincoln Street which is shown in red. The other new road will go to City Hall and be parallel to Elm Street which is also shown in red. Give the coordinates for the location of the park.
Type below:
_______________

Answer:

By seeing we can say that the coordinates for the location of the park is (1,1)

Question 7.
Each unit of the coordinate plane represents 2 miles. How far will the park be from City Hall?
________ miles

Answer: 8 units

Explanation:
The distance from City Hall to Park is 4 units.
Each unit = 2 miles
So, 2 miles × 4 = 8 miles
The distance from City Hall to Park is 8 miles.

Question 8.
\(\overline { PQ } \) is one side of right triangle PQR. In the triangle, ∠P is the right angle, and the length of side \(\overline { PR } \) is 3 units. Give all the possible coordinates for vertex R.

Type below:
_______________

Answer:

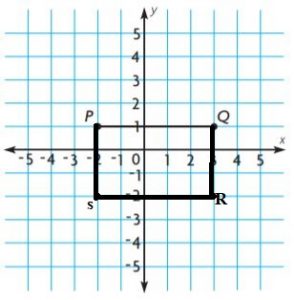
The coordinates of S are (-2,-2)
The coordinates of R are (3,-2)

Question 9.
Use Math Vocabulary Quadrilateral WXYZ has vertices with coordinates W(−4, 0), X(−2, 3), Y(2, 3), and Z(2, 0). Classify the quadrilateral using the most exact name possible and explain your answer.
Type below:
_______________

Answer: Trapezoid

By seeing the above graph we can say that a suitable quadrilateral is a trapezoid.

Question 10.
Kareem is drawing parallelogram ABCD on the coordinate plane. Find and label the coordinates of the fourth vertex, D, of the parallelogram. Draw the parallelogram. What is the length of side CD? How do you know?

Type below:
_______________

Answer:

Figures on the Coordinate Plane – Page No. 587

Question 1.
The vertices of triangle DEF are D(−2, 3), E(3, −2), and F(−2, −2). Graph the triangle, and find the length of side \(\overline { DF } \).
________ units

Answer: 5 units

Explanation:
Vertical distance of D from 0: |3| = 3 units
Vertical Distance of F from 0: |-2| = 2 units
The points are in different quadrants, so add to find the distance from D to F: 3 + 2 = 5

Graph the figure and find the length of side \(\overline { BC } \).

Question 2.
A(1, 4), B(1, −2), C(−3, −2), D(−3, 3)
________ units

Answer: 4 units

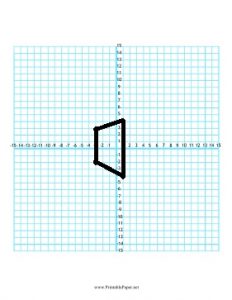
Question 3.
A(−1, 4), B(5, 4), C(5, 1), D(−1, 1)
________ units

Answer: 3 units

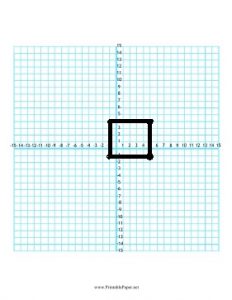
Problem Solving

Question 4.
On a map, a city block is a square with three of its vertices at (−4, 1), (1, 1), and (1, −4). What are the coordinates of the remaining vertex?
Type below:
_______________

Answer: (-4, -4)

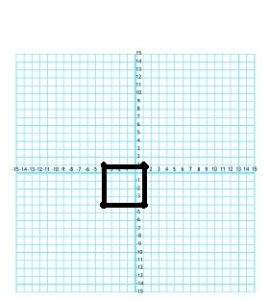
Question 5.
A carpenter is making a shelf in the shape of a parallelogram. She begins by drawing parallelogram RSTU on a coordinate plane with vertices R(1, 0), S(−3, 0), and T(−2, 3). What are the coordinates of vertex U?
Type below:
_______________

Answer: (2, 3)

Question 6.
Explain how you would find the fourth vertex of a rectangle with vertices at (2, 6), (−1, 4), and (−1, 6).
Type below:
_______________

Answer:

Explanation:
Midpoint of AC = (2 + (-1))/2 = 1/2; (6 + 6)/2 = 6
Midpoint of AC = (1/2, 6)
Midpoint of BD = (-1 + a)/2 = (-1 + a)/2; (b + 4)/2
(-1 + a)/2 = 1/2
-1 + a = 1
a = 2
(b + 4)/2 = 6
b + 4 = 12
b = 12 – 4
b = 8
So, the fouth vertex D is (2, 8)

Lesson Check – Page No. 588

Question 1.
The coordinates of points M, N, and P are M(–2, 3), N(4, 3), and P(5, –1). What coordinates for point Q make MNPQ a parallelogram?
Type below:
_______________

Answer: Q (-1, -1)

Question 2.
Dirk draws quadrilateral RSTU with vertices R(–1, 2), S(4, 2), T(5, –1), and U( 2, –1). Which is the best way to classify the quadrilateral?
Type below:
_______________

Answer:
The bases and height are not equal.
So, the best way to classify the quadrilateral is Trapezoid.

Spiral Review

Question 3.
Marcus needs to cut a 5-yard length of yarn into equal pieces for his art project. Write an equation that models the length l in yards of each piece of yarn if Marcus cuts it into p pieces.
Type below:
_______________

Answer:
Given,
Marcus needs to cut a 5-yard length of yarn into equal pieces for his art project.
To find the length we have to divide 5 by p.
Thus the equation is l = 5 ÷ p

Question 5.
A trapezoid is 6 \(\frac{1}{2}\) feet tall. Its bases are 9.2 feet and 8 feet long. What is the area of the trapezoid?
________ ft²

Answer: 55.9

Explanation:
Given that,
A trapezoid is 6 \(\frac{1}{2}\) feet tall. Its bases are 9.2 feet and 8 feet long.
We know that
Area of trapezoid = (b1 + b2)h/2
A = (9.2 + 8)6.5/2
A = (17.2 × 6.5)/2
A = 55.9 ft²

Question 6.
The dimensions of the rectangle below will be multiplied by 3. How will the area be affected?

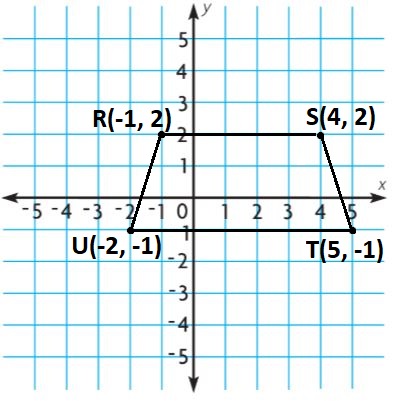
Type below:
_______________

Answer:
3 × 3 = 9
the area will be multiplied by 9.

Chapter 10 Review/Test – Page No. 589

Question 1.
Find the area of the parallelogram.

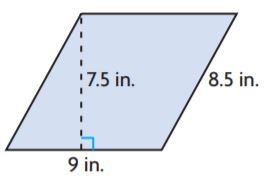
________ in.²

Answer: 67.5

Explanation:
b = 9 in
h = 7.5 in
Area of the parallelogram is bh
A = 9 in × 7.5 in
A = 67.5 sq. in
Thus the area of the parallelogram is 67.5 in.²

Question 2.
A wall tile is two different colors. What is the area of the white part of the tile? Explain how you found your answer.

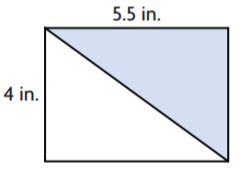
________ in.²

Answer: 11 in.²

Explanation:
b = 5.5 in
h = 4 in
We know that
The area of the triangle is bh/2
A = (5.5 in × 4 in)/2
A = 22/2 sq. in
A = 11 sq. in
Thus the area of one triangle is 11 in.²

Question 3.
The area of a triangle is 36 ft². For numbers 3a–3d, select Yes or No to tell if the dimensions could be the height and base of the triangle.
3a. h = 3 ft, b = 12 ft
3b. h = 3 ft, b = 24 ft
3c. h = 4 ft, b = 18 ft
3d. h = 4 ft, b = 9 ft
3a. ____________
3b. ____________
3c. ____________
3d. ____________

Answer:
3a. No
3b. Yes
3c. Yes
3d. No

Explanation:
The area of a triangle is 36 ft².
3a. h = 3 ft, b = 12 ft
The area of the triangle is bh/2
A = (12 × 3)/2
A = 6 × 3 = 18
A = 18 sq. ft
Thus the answer is no.
3b. h = 3 ft, b = 24 ft
The area of the triangle is bh/2
A = (3 × 24)/2
A = 3 × 12
A = 36 sq. ft
Thus the answer is yes.
3c. h = 4 ft, b = 18 ft
The area of the triangle is bh/2
A = (4 × 18)/2
A = 4 × 9
A = 36 sq. ft
Thus the answer is yes.
3d. h = 4 ft, b = 9 ft
The area of the triangle is bh/2
A = (4 × 9)/2
A = 2 ft × 9 ft
A = 18 sq. ft
Thus the answer is no.

Question 4.
Mario traced this trapezoid. Then he cut it out and arranged the trapezoids to form a rectangle. What is the area of the rectangle?

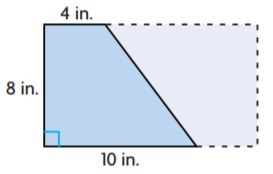
________ in.²

Answer: 112

Explanation:
b1 = 10 in
b2 = 4 in
h = 8 in
We know that
Area of trapezoid = (b1 + b2)h/2
A = (10 in + 4 in)8 in/2
A = 14 in × 4 in
A = 56 sq. in
Thus the area of the trapezoid for the above figure is 56 sq. in

Chapter 10 Review/Test Page No. 590

Question 5.
The area of the triangle is 24 ft². Use the numbers to label the height and base of the triangle.

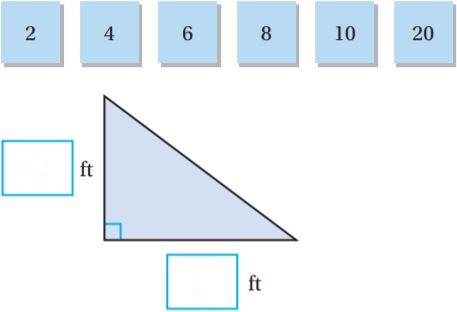
Type below:
_______________

Answer: 6, 8

Explanation:

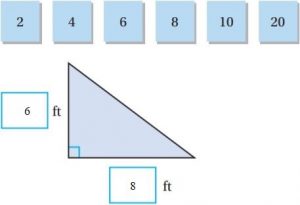
Area of the triangle = bh/2
A = (6 ft × 8 ft)/2
A = 6 ft × 4 ft
A = 24 ft²

Question 6.
A rectangle has an area of 50 cm². The dimensions of the rectangle are multiplied to form a new rectangle with an area of 200 cm². By what number were the dimensions multiplied?
Type below:
_______________

Answer: 2

Explanation:
Let A₁ = the original area a
and A₂ = the new area
and n = the number by which the dimensions were multiplied
A₁ = lw
A₂ = nl × nw = n²lw
A₂/A₁ = (n²lw)/(lw) = 200/50
n² = 4
n = 2

Question 7.
Sami put two trapezoids with the same dimensions together to make a parallelogram.

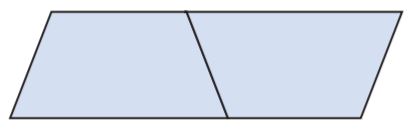
The formula for the area of a trapezoid is \(\frac{1}{2}\)(b₁ + b₂)h. Explain why the bases of a trapezoid need to be added in the formula.
Type below:
_______________

Answer:
A trapezoid is a 4-sided figure with one pair of parallel sides. To find the area of a trapezoid, take the sum of its bases, multiply the sum by the height
sum by the height of the trapezoid, and then divide the result by 2.

Question 8.
A rectangular plastic bookmark has a triangle cut out of it. Use the diagram of the bookmark to complete the table.


Type below:
_______________

Answer: 10 – 0.5 = 9.5

Chapter 10 Review/Test Page No. 591

Question 10.
A pillow is in the shape of a regular pentagon. The front of the pillow is made from 5 pieces of fabric that are congruent triangles. Each triangle has an area of 22 in.². What is the area of the front of the pillow?
________ in.²

Answer: 110 in.²

Explanation:
Given,
Each triangle has an area of 22 in.²
The front of the pillow is made from 5 pieces of fabric that are congruent triangles.
Area of front pillow = 5 × 22 in.² = 110 in.²

Question 11.
Which expressions can be used to find the area of the trapezoid? Mark all that apply.

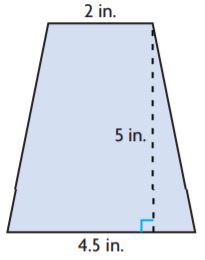
Options:
a. \(\frac{1}{2}\) × (5 + 2) × 4.5
b. \(\frac{1}{2}\) × (2 + 4.5) × 5
c. \(\frac{1}{2}\) × (5 + 4.5) × 2
d. \(\frac{1}{2}\) × (6.5) × 5

Answer: \(\frac{1}{2}\) × (2 + 4.5) × 5

Explanation:
b1 = 4.5 in
b2 = 2
h = 5 in
We know that,
Area of trapezoid = (b1 + b2)h/2
A = \(\frac{1}{2}\) × (2 + 4.5) × 5
Thus the correct answer is option B.

Question 12.
Name the polygon and find its area. Show your work.

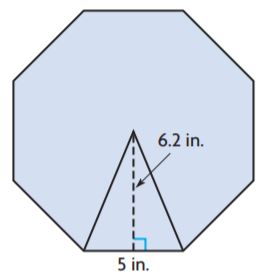
Type below:
_______________

Answer: 31 sq. in.

Explanation:
b = 5 in
h = 6.2 in
The area of the triangle is bh/2
A = (5 × 6.2)/2
A = 31/2
A = 15.5 sq. in
There are 2 triangles.
To find the area of the regular polygon we have to multiply the area of the triangle and number of triangles.
A = 15.5 × 2 = 31

Chapter 10 Review/Test Page No. 592

Question 13.
A carpenter needs to replace some flooring in a house.

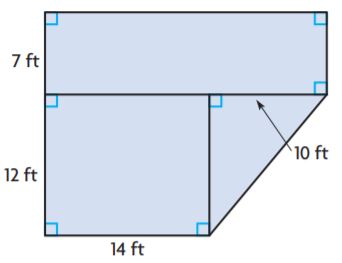
Select the expression that can be used to find the total area of the flooring to be replaced. Mark all that apply.
Options:
a. 19 × 14
b. 168 + 12 × 14 + 60
c. 19 × 24 − \(\frac{1}{2}\) × 10 × 12
d. 7 × 24 + 12 × 14 + \(\frac{1}{2}\) × 10 × 12

Answer: B, C, D

Explanation:

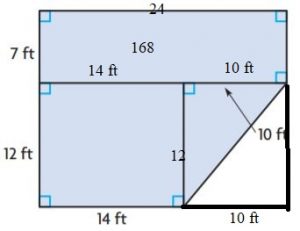
Here we have to use the Area of the parallelogram, Area of the rectangle, and area of triangle formulas.
Thus the suitable answers are 168 + 12 × 14 + 60, 19 × 24 − \(\frac{1}{2}\) × 10 × 12 and 7 × 24 + 12 × 14 + \(\frac{1}{2}\) × 10 × 12.

Question 14.
Ava wants to draw a parallelogram on the coordinate plane. She plots these 3 points.

Part A
Find and label the coordinates of the fourth vertex, K, of the parallelogram. Draw the parallelogram
Type below:
_______________

Answer: K (2, 1)

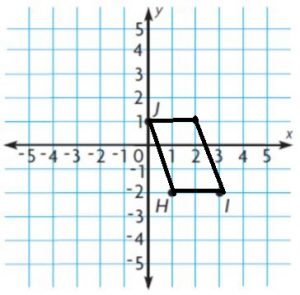
Question 14.
Part B
What is the length of side JK? How do you know?
Type below:
_______________

Answer:
By using the above graph we can find the length of JK.
The length of the JK is 2 units.

Chapter 10 Review/Test Page No. 593

Question 15.
Joan wants to reduce the area of her posters by one-third. Draw lines to match the original dimensions in the left column with the correct new area in the right column. Not all dimensions will have a match.

Type below:
_______________

Answer:

Question 16.
Alex wants to enlarge a 4-ft by 6-ft vegetable garden by multiplying the dimensions of the garden by 2.
Part A
Find each area.
Area of original garden : ________ ft²
Area of enlarged garden : ________ ft²

Answer:
B = 4 ft
w = 6 ft
Area of original garden = 4 ft × 6 ft
A = 24 sq. ft
Now multiply 2 to base and width
b = 4 × 2 = 8 ft
w = 6 × 2 = 12 ft
Area of original garden = bw
A = 8 ft × 12 ft
A = 96 sq. ft

Question 16.
Suppose the point (3, 2) is changed to (3, 1) on this rectangle. What other point must change so the figure remains a rectangle? What is the area of the new rectangle?

Type below:
_______________

Answer:
Point: (-2, 2) would change to (-2, 1)
Rectangle:
B = 5 units
W = 4 units
Area of the rectangle = b × w
A = 5 × 4 = 20
A = 20 sq. units

Chapter 10 Review/Test Page No. 594

Question 18.
Look at the figure below. The area of the parallelogram and the areas of the two congruent triangles formed by a diagonal are related. If you know the area of the parallelogram, how can you find the area of one of the triangles?

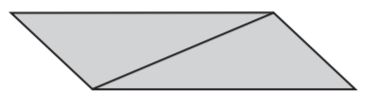
Type below:
_______________

Answer:
Each of the diagonals of a parallelogram divides it into two congruent triangles, as we saw when we proved properties like that the opposite sides are equal to each other or that the two pairs of opposite angles are congruent. Since those two triangles are congruent, their areas are equal.
We also saw that the diagonals of the parallelogram bisect each other, and so create two additional pairs of congruent triangles.
When comparing the ratio of areas of triangles, we often look for an equal base or an equal height.

Question 20.
Eliana is drawing a figure on the coordinate grid. For numbers 20a–20d, select True or False for each statement.
20a. The point (−1, 1) would be the fourth vertex of a square.
20b. The point (1, 1) would be the fourth vertex of a trapezoid.
20c. The point (2, -1) would be the fourth vertex of a trapezoid.
20d. The point (−1, -1) would be the fourth vertex of a square.
20a. ____________
20b. ____________
20c. ____________
20d. ____________

Answer:
20a. False
20b. False
20c. True
20d. True

Conclusion:

With the help of the above-provided links you can complete the homework within time without any mistakes. Test your knowledge by solving the problems mentioned in our website. Stay with us to get the solution keys of all Go Math Grade 6 Chapters from 1 to 13.