Model Ratios are an interesting topic in Grade 6. The students who are in search of Go Math Grade 6 Answer Key Chapter 4 Model Ratios can get them on this page. The best and quick way of learning is possible with Go Math Grade 6 Chapter 4 Model Ratios Answer Key. We have provided the solutions for all the questions in an easy manner in our Go Math Grade 6 Chapter 4 Model Ratios Solution Key. Get Free Access to Download Go Math Grade 6 Chapter 4 Model Ratios Solution Key PDF @ ccssanswers.com Thus make use of the links and Download HMH Go math Grade 6 answer key chapter 4 model ratios and get the best results.
Go Math Grade 6 Chapter 4 Model Ratios Answer Key
The easy-solving of math problems will help you to understand all the difficult problems. So, begin your practice now and be on the top list to score good marks in the exam. Use Go Math 6 Standard Answer Key Chapter 4 Model Ratios handy solutions to learn deep maths online or offline. Come and fall in love with maths by practicing the problems from HMH Go Math 6th Grade Chapter 4 Model Ratios Answer Key. Hit the links and start your preparation now.
Lesson 1: Investigate • Model Ratios
- Model Ratios – Page No. 213
- Model Ratios – Page No. 214
- Model Ratios – Page No. 215
- Model Ratios Lesson Check – Page No. 216
Lesson 2: Ratios and Rates
- Ratios and Rates – Page No. 219
- Ratios and Rates – Page No. 220
- Ratios and Rates – Page No. 221
- Ratios and Rates Lesson Check – Page No. 222
Lesson 3: Equivalent Ratios and Multiplication Tables
- Equivalent Ratios and Multiplication Tables – Page No. 225
- Equivalent Ratios and Multiplication Tables – Page No. 226
- Equivalent Ratios and Multiplication Tables – Page No. 227
- Equivalent Ratios and Multiplication Tables Lesson Check – Page No. 228
Lesson 4: Problem Solving • Use Tables to Compare Ratios
- Use Tables to Compare Ratios – Page No. 231
- Use Tables to Compare Ratios – Page No. 232
- Use Tables to Compare Ratios – Page No. 233
- Use Tables to Compare Ratios Lesson Check – Page No. 234
Lesson 5: Algebra • Use Equivalent Ratios
- Use Equivalent Ratios – Page No. 237
- Use Equivalent Ratios – Page No. 238
- Use Equivalent Ratios – Page No. 239
- Use Equivalent Ratios Lesson Check – Page No. 240
Mid-Chapter Checkpoint
Lesson 6: Find Unit Rates
- Find Unit Rates – Page No. 245
- Find Unit Rates – Page No. 246
- Find Unit Rates – Page No. 247
- Find Unit Rates Lesson Check – Page No. 248
Lesson 7: Algebra • Use Unit Rates
- Use Unit Rates – Page No. 251
- Use Unit Rates – Page No. 252
- Use Unit Rates – Page No. 253
- Use Unit Rates Lesson Check – Page No. 254
Lesson 8: Algebra • Equivalent Ratios and Graphs
- Equivalent Ratios and Graphs – Page No. 257
- Equivalent Ratios and Graphs – Page No. 258
- Equivalent Ratios and Graphs – Page No. 259
- Equivalent Ratios and Graphs Lesson Check – Page No. 260
Chapter 4 Review/Test
- Review/Test – Page No. 261
- Review/Test – Page No. 262
- Review/Test – Page No. 263
- Review/Test – Page No. 264
- Review/Test – Page No. 265
- Review/Test – Page No. 266
Share and Show – Page No. 213
Write the ratio of yellow counters to red counters.
Question 1.

Type below:
___________
Answer:
1: 2
Explanation:
There are one yellow counter and two red counters.
So, the ratio is 1:2
Question 2.

Type below:
___________
Answer:
5: 3
Explanation:
There are 5 yellow counter and 3 red counters.
So, the ratio is 5:3
Draw a model of the ratio.
Question 3.
3 : 2
Type below:
___________
Answer:

Explanation:
As the ratio is 3:2, we can draw three yellow counters and 2 red counters.
Question 4.
1 : 5
Type below:
___________
Answer:

Explanation:
As the ratio is 1:5, we can draw 1 yellow counter and 5 red counters.
Use the ratio to complete the table.
Question 5.
Wen is arranging flowers in vases. For every 1 rose she uses, she uses 6 tulips. Complete the table to show the ratio of roses to tulips.
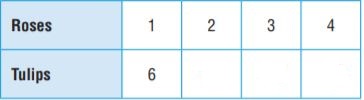
Type below:
___________
Answer:
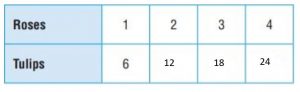
Explanation:
There is 1 box for every 6 Tulips.
The ratio is 1 : 6.
Each time the number of boxes increases by 1, the number of Tulips increases by 6
So, for 2 boxes, 6 + 6 = 12 Tulips
For 3 boxes, 12 + 6 = 18 Tulips
For 4 boxes, 18 + 6 = 24 Tulips
Question 6.
On the sixth-grade field trip, there are 8 students for every 1 adult. Complete the table to show the ratio of students to adults.
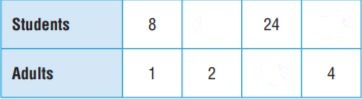
Type below:
___________
Answer:
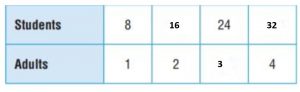
Explanation:
There is 1 adult out of 8 Students.
The ratio is 8:1.
Each time the number of students increases double, the number of adults becomes double.
So, for 8 + 8 = 16 students, 2 Adults available
For 16 + 8 = 24 students, 2 + 1 = 3 Adults available
For 24 + 8 = 32 students, 3 + 1 = 4 Adults available
Question 7.
Zena adds 4 cups of flour for every 3 cups of sugar in her recipe. Draw a model that compares cups of flour to cups of sugar.
Type below:
___________
Answer:
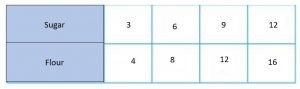
Explanation:
Zena adds 4 cups of flour for every 3 cups of sugar in her recipe.
For every 3 cups of sugar, she adds 4 cups of flour.
For 6 cups of sugar, she adds 8 cups of flour
For 9 cups of sugar, she adds 12 cups of flour
For 12 cups of sugar, she adds 16 cups of flour
Draw Conclusions – Page No. 214
The reading skill draw conclusions can help you analyze and make sense of information.
Hikers take trail mix as a snack on long hikes because it is tasty, nutritious, and easy to carry. There are many different recipes for trail mix, but it is usually made from different combinations of dried fruit, raisins, seeds, and nuts. Tanner and his dad make trail mix that has 1 cup of raisins for every 3 cups of sunflower seeds.
Question 8.
Model Mathematics Explain how you could model the ratio that compares cups of raisins to cups of sunflower seeds when Tanner uses 2 cups of raisins.
Type below:
___________
Answer:
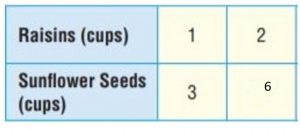
Explanation:
Hikers take trail mix as a snack on long hikes because it is tasty, nutritious, and easy to carry. There are many different recipes for trail mix, but it is usually made from different combinations of dried fruit, raisins, seeds, and nuts. Tanner and his dad make trail mix that has 1 cup of raisins for every 3 cups of sunflower seeds.
For 2 cups of raisins, he needs 3 + 3 = 6 cups of sunflower seeds
The table shows the ratio of cups of raisins to cups of sunflower seeds for different amounts of trail mix. Model each ratio as you complete the table.
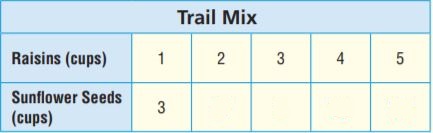
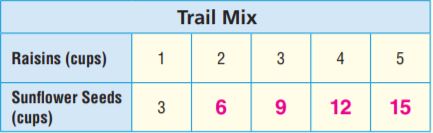
Question 9.
Describe the pattern you see in the table.
Type below:
___________
Answer:
Multiply Raisins by 3 to get number of Sunflower Seeds.
Question 10.
Draw Conclusions What conclusion can Tanner draw from this pattern?
Type below:
___________
Answer:
He needs 3 times as many seeds as raisins

Model Ratios – Page No. 215
Write the ratio of gray counters to white counters.
Question 1.

Type below:
___________
Answer:
3:4
Explanation:
There are 3 gray counter and 4 white counters.
So, the ratio is 3:4
Question 2.

Type below:
___________
Answer:
4:1
Explanation:
There are 4 gray counter and 1 white counter.
So, the ratio is 4:1
Question 3.

Type below:
___________
Answer:
2:3
Explanation:
There are 2 gray counter and 3 white counters.
So, the ratio is 2:3
Draw a model of the ratio.
Question 4.
5 : 1
Type below:
___________
Answer:

Explanation:
As the ratio is 5:1, we can draw 5 yellow counters and 1 red counter.
Question 5.
6 : 3
Type below:
___________
Answer:

Explanation:
As the ratio is 6:3, we can draw 6 yellow counters and 3 red counters.
Use the ratio to complete the table.
Question 6.
Marc is assembling gift bags. For every 2 pencils he places in the bag, he uses 3 stickers. Complete the table to show the ratio of pencils to stickers.

Type below:
___________
Answer:

Explanation:
Marc is assembling gift bags. For every 2 pencils he places in the bag, he uses 3 stickers.
For 4 pencils, he uses 3 + 3 = 6 stickers
For 6 pencils, he uses 6 + 3 = 9 stickers
For 8 pencils, he uses 9 + 3 = 12 stickers
Question 7.
Singh is making a bracelet. She uses 5 blue beads for every 1 silver bead. Complete the table to show the ratio of blue beads to silver beads

Type below:
___________
Answer:

Explanation:
Singh is making a bracelet. She uses 5 blue beads for every 1 silver bead.
For 2 silver bead, she uses 5 + 5 = 10 blue beads.
For 3 silver bead, she uses 10 + 5 = 15 blue beads.
For 4 silver bead, she uses 15 + 5 = 20 blue beads.
Problem Solving
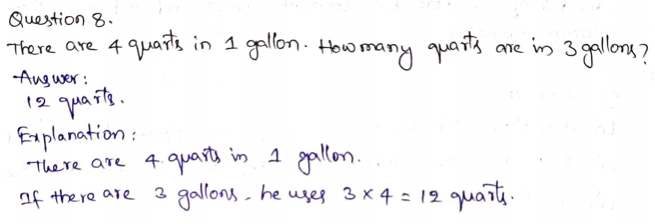

Question 10.
Suppose there was 1 centerpiece for every 5 tables. Use counters to show the ratio of centerpieces to tables. Then make a table to find the number of tables if there are 3 centerpieces.
Type below:
___________
Answer:

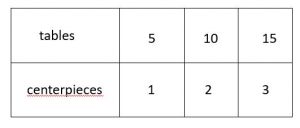
Explanation:
Suppose there was 1 centerpiece for every 5 tables.
If there are 3 centerpieces, 5 × 3 = 15 tables
Lesson Check – Page No. 216
Question 1.
Francine is making a necklace that has 1 blue bead for every 6 white beads. How many white beads will she use if she uses 11 blue beads?
______ white beads
Answer:
66 white beads
Explanation:
Francine is making a necklace that has 1 blue bead for every 6 white beads.
11 × 6 = 66 white beads

Spiral Review
Question 3.
Louis has 45 pencils and 75 pens to divide into gift bags at the fair. He does not want to mix the pens and pencils. He wants to place an equal amount in each bag. What is the greatest number of pens or pencils he can place in each bag?
______
Answer:
Louis can form at most 15 bags, each of which will contain 3 pencils and 5 pens.
Explanation:
Louis has 45 pencils and 75 pens to divide into gift bags at the fair. He does not want to mix the pens and pencils. He wants to place an equal amount in each bag.
Factor both these numbers:
45 = 3·3·5;
75 = 3·5·5.
The greatest common factor (write all common factors and multiply them) is 3·5=15. Then:
45=15·3;
75=15·5.
Louis can form at most 15 bags, each of them will contain 3 pencils and 5 pens.
Question 4.
Of the 24 students in Greg’s class, \(\frac{3}{8}\) ride the bus to school. How many students ride the bus?
______ students
Answer:
9 students
Explanation:
Of the 24 students in Greg’s class, \(\frac{3}{8}\) ride the bus to school.
3/8 x 24= 9
Question 5.
Elisa made 0.44 of the free throws she attempted. What is that amount written as a fraction in simplest form?
\(\frac{□}{□}\)
Answer:
\(\frac{11}{25}\)
Explanation:
Elisa made 0.44 of the free throws she attempted.
0.44 = 44/100
44/100 = 22/50 = 11/25
11/25
Question 6.
On a coordinate plane, the vertices of a rectangle are (–1, 1), (3, 1), (–1, –4), and (3, –4). What is the perimeter of the rectangle?
______ units
Answer:
18 units
Explanation:
On a coordinate plane, the vertices of a rectangle are (–1, 1), (3, 1), (–1, –4), and (3, –4).
|-1| = 1
The distance from (–1, 1), (3, 1) is 1 + 0 + 0 + 3 = 4
|-4| = 4
The distance from (3, 1), (3, –4) is 1 + 0 + 0 + 4 = 5
perimeter of the rectangle = 4 + 5 + 5 + 4 = 18
Share and Show – Page No. 219
Question 1.
Write the ratio of the number of red bars to blue stars.

\(\frac{□}{□}\)
Answer:
\(\frac{8}{3}\)
Explanation:
There are 8 stars and 3 red boxes.
So, the ratio is 8:3
Write the ratio in two different ways.
Question 2.
8 to 16
Type below:
___________
Answer:
\(\frac{8}{16}\)
8:16
Explanation:
8 to 16 as a fraction of 8/16
8 to 16 with a colon 8:16
Question 3.
\(\frac{4}{24}\)
Type below:
___________
Answer:
4 to 24
4:24
Explanation:
\(\frac{4}{24}\) using words 4 to 24
\(\frac{4}{24}\) with a colon 4:24
Question 4.
1 : 3
Type below:
___________
Answer:
1 to 3
\(\frac{1}{3}\)
Explanation:
1 : 3 using words 1 to 3
1 : 3 as a fraction 1/3
Question 5.
7 to 9
Type below:
___________
Answer:
\(\frac{7}{9}\)
7:9
Explanation:
7 to 9 as a fraction 7/9
7 to 9 with a colon 7:9
Question 6.
Marilyn saves $15 per week. Complete the table to find the rate that gives the amount saved in 4 weeks. Write the rate in three different ways.
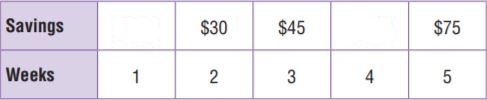
Type below:
___________
Answer:
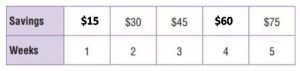
Explanation:
Marilyn saves $15 per week.
for 4 weeks, $15 × 4 = $60
On Your Own
Write the ratio in two different ways.
Question 7.
\(\frac{16}{40}\)
Type below:
___________
Answer:
16 to 40
16:40
Explanation:
\(\frac{16}{40}\) using words 16 to 40
\(\frac{16}{40}\) with a colon 16:40
Question 8.
8 : 12
Type below:
___________
Answer:
8 to 12
\(\frac{8}{12}\)
Explanation:
8 : 12 using words 8 to 12
8 : 12 as a fraction \(\frac{8}{12}\)
Question 9.
4 to 11
Type below:
___________
Answer:
\(\frac{4}{11}\)
4:11
Explanation:
4 to 11 as a fraction \(\frac{4}{11}\)
4 to 11 with a colon 4:11
Question 10.
2 : 13
Type below:
___________
Answer:
2 to 13
\(\frac{2}{13}\)
Explanation:
2 : 13 using words 2 to 13
2 : 13 as a fraction \(\frac{2}{13}\)
Question 11.
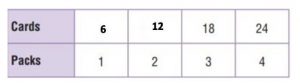
There are 24 baseball cards in 4 packs. Complete the table to find the rate that gives the number of cards in 2 packs. Write this rate in three different ways.
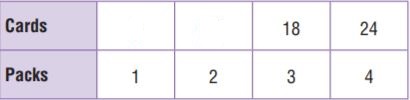
Type below:
___________
Answer:
Explanation:
There are 24 baseball cards in 4 packs.
For 2 packs, (2 × 24)/4 = 12
For 1 pack, (1× 24)/4 = 6

Problem Solving + Applications – Page No. 220
Use the diagram of a birdhouse for 13–15.
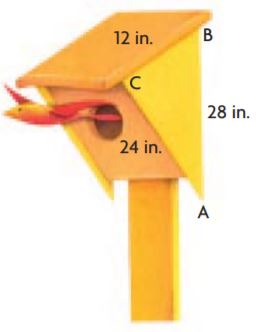
Question 13.
Write the ratio of AB to BC in three different ways.
Type below:
___________
Answer:
28 : 12, 28 to 12, \(\frac{2}{13}\)
Explanation:
AB = 28 in
BC = 12 in
AB : BC = 28 : 12, 28 to 12, \(\frac{2}{13}\)
Question 14.
Write the ratio of the shortest side length of triangle ABC to the perimeter of the triangle in three different ways.
Type below:
___________
Answer:
12 : 64, 12 to 64, \(\frac{12}{64}\)
Explanation:
the shortest side length of triangle ABC = 12 in
the perimeter of the triangle 12 + 28 + 24 = 64
12 : 64, 12 to 64, \(\frac{12}{64}\)
Question 15.
Represent a Problem Write the ratio of the perimeter of triangle ABC to the longest side length of the triangle in three different ways.
Type below:
___________
Answer:
64 : 28, 64 to 28, \(\frac{64}{28}\)
Explanation:
the ratio of the perimeter of triangle ABC = 12 + 28 + 24 = 64
the longest side length of the triangle = 28 in
64 : 28, 64 to 28, \(\frac{64}{28}\)

Question 17.
What’s the Question? The ratio of total students in Ms. Murray’s class to students in the class who have an older brother is 3 to 1. The answer is 1:2. What is the question?
Type below:
___________
Answer:
What is the ratio of students in the class who don’t have an older brother to students in the class with an older brother?

Question 19.
Julia has 2 green reusable shopping bags and 5 purple reusable shopping bags. Select the ratios that compare the number of purple reusable shopping bags to the total number of reusable shopping bags. Mark all that apply.
- 5 to 7
- 5 : 7
- 5 : 2
- \(\frac{2}{5}\)
- 2 to 7
- \(\frac{5}{7}\)
Type below:
___________
Answer:
5 to 7, 5 : 7, \(\frac{5}{7}\)
Explanation:
the number of purple reusable shopping bags = 5
the total number of reusable shopping bags = 5 + 2 = 7
5 to 7, 5 : 7, \(\frac{5}{7}\)
Ratios and Rates – Page No. 221
Write the ratio in two different ways.
Question 1.
\(\frac{4}{5}\)
Type below:
___________
Answer:
4 to 5
4 : 5
Explanation:
\(\frac{4}{5}\) using words 4 to 5
\(\frac{4}{5}\) with a colon 4 : 5
Question 2.
16 to 3
Type below:
___________
Answer:
\(\frac{16}{3}\)
16 : 3
Explanation:
16 to 3 as a fraction \(\frac{16}{3}\)
16 to 3 with a colon 16 : 3
Question 3.
9 : 13
Type below:
___________
Answer:
9 to 13
\(\frac{9}{13}\)
Explanation:
9 : 13 using words 9 to 13
9 : 13 as a fraction \(\frac{9}{13}\)
Question 4.
\(\frac{15}{8}\)
Type below:
___________
Answer:
15 to 8
15 : 8
Explanation:
\(\frac{15}{8}\) using words 15 to 8
\(\frac{15}{8}\) with a colon 15 : 8
Question 5.
There are 20 light bulbs in 5 packages. Complete the table to find the rate that gives the number of light bulbs in 3 packages. Write this rate in three different ways.

Type below:
___________
Answer:

Explanation:
There are 20 light bulbs in 5 packages.
For 1 package, 4 light bulbs available
For 2 package, 8 light bulbs available
For 3 package, 12 light bulbs available
For 4 package, 16 light bulbs available
Problem Solving
Question 6.
Gemma spends 4 hours each week playing soccer and 3 hours each week practicing her clarinet. Write the ratio of hours spent practicing clarinet to hours spent playing soccer three different ways.
Type below:
___________
Answer:
\(\frac{3}{4}\), 3 : 4, 3 to 4
Explanation:
Gemma spends 4 hours each week playing soccer and 3 hours each week practicing her clarinet.
3/4, 3 : 4, 3 to 4
Question 7.
Randall bought 2 game controllers at Electronics Plus for $36. What is the unit rate for a game controller at Electronics Plus?
Type below:
___________
Answer:
\(\frac{$18}{1}\)
Explanation:
Randall bought 2 game controllers at Electronics Plus for $36. $36/2 = $18/1 is the unit rate for a game controller at Electronics Plus
Question 8.
Explain how to determine if a given rate is also a unit rate.
Type below:
___________
Answer:
when rates are expressed as a quantity of 1, such as 2 feet per second or 5 miles per hour, they are called unit rates. If you have a multiple-unit rate such as 120 student for every 3 buses, an want to find the single-unit rate, write a ratio equal to the multiple-unit rate with 1 as the second term
Lesson Check – Page No. 222
Question 1.
At the grocery store, Luis bought 10 bananas and 4 apples. What are three different ways to write the ratio of apples to bananas?
Type below:
___________
Answer:
4 : 10, 4 to 10, \(\frac{4}{10}\)
Explanation:
At the grocery store, Luis bought 10 bananas and 4 apples. 4/10, 4 : 10, 4 to 10
Question 2.
Rita checked out 7 books from the library. She had 2 non-fiction books. The rest were fiction. What are three different ways to write the ratio of non-fiction to fiction?
Type below:
___________
Answer:
2 to 5, 2 : 5, \(\frac{2}{5}\)
Explanation:
Rita checked out 7 books from the library. She had 2 non-fiction books. The rest were fiction.
fiction = 5
2 to 5, 2 : 5, \(\frac{2}{5}\)
Spiral Review
Question 3.
McKenzie bought 1.2 pounds of coffee for $11.82. What was the cost per pound?
$ ______
Answer:
$9.85
Explanation:
McKenzie bought 1.2 pounds of coffee for $11.82. $11.82/1.2 = $9.85
Question 5.
Gina draws a map of her town on a coordinate plane. The point that represents the town’s civic center is 1 unit to the right of the origin and 4 units above it. What are the coordinates of the point representing the civic center?
Type below:
___________
Answer:
(-1, 4)
Explanation:
Gina draws a map of her town on a coordinate plane. The point that represents the town’s civic center is 1 unit to the right of the origin and 4 units above it.
(-1, 4)
Question 6.
Stefan draws these shapes. What is the ratio of triangles to stars?

Type below:
___________
Answer:
2 to 5
Explanation:
There are 2 triangles and 5 stars. So, the ratio is 2 : 5
Share and Show – Page No. 225
Write two equivalent ratios.
Question 1.
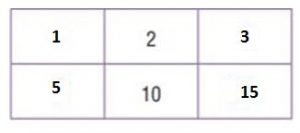
Use a multiplication table to write two ratios that are equivalent to \(\frac{4}{7}\).
Type below:
___________
Answer:
\(\frac{4}{7}\) = \(\frac{8}{14}\), \(\frac{12}{21}\)
Explanation:
The original ratio is 4/7. Shade the row for 4 and the row for 7 on the multiplication table.
The column for 2 shows there are 2 ∙ 4, when there are 2 ∙ 7. So, 4/7 equal to 8/14
The column for 3 shows there are 3 ∙ 4, when there are 3 ∙ 7. So, 4/7 equal to 12/21
Question 2.
Type below:
___________
Answer:
Explanation:
The original ratio is 3/7. Shade the row for 3 and the row for 7 on the multiplication table.
The column for 2 shows there are 2 ∙ 3, when there are 2 ∙ 7. So, 3/7 equal to 6/14
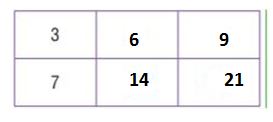
The column for 3 shows there are 3 ∙ 3, when there are 3 ∙ 7. So, 3/7 equal to 9/21
Question 3.
Type below:
___________
Answer:
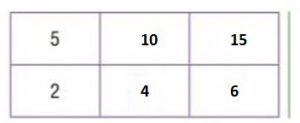
Explanation:
The original ratio is 5/2. Shade the row for 5 and the row for 2 on the multiplication table.
The column for 2 shows there are 2 ∙ 5 when there are 2 ∙ 2. So, 5/2 equal to 10/4
The column for 3 shows there are 3 ∙ 5 when there are 3 ∙ 2. So, 5/2 equal to 15/6
Question 4.
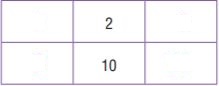
Type below:
___________
Answer:
Explanation:
The original ratio is 2/10. Shade the row for 2 and the row for 10 on the multiplication table.
The column for 1 shows there are 1 ∙ 2 when there are 5 ∙ 2. So, 2/10 equal to 1/5
The column for 3 shows there are 1 ∙ 3 when there are 5 ∙ 3. So, 2/10 equal to 3/15
Question 5.
\(\frac{4}{5}\)
Type below:
___________
Answer:
\(\frac{4}{5}\) = \(\frac{8}{10}\), \(\frac{12}{15}\)
Explanation:
The original ratio is 4/5. Shade the row for 4 and the row for 5 on the multiplication table.
The column for 2 shows there are 2 ∙ 4, when there are 2 ∙ 5. So, 4/5 equal to 8/10
The column for 3 shows there are 3 ∙ 4, when there are 3 ∙ 5. So, 4/5 equal to 12/15
Question 6.
\(\frac{12}{30}\)
Type below:
___________
Answer:
\(\frac{12}{30}\) = \(\frac{24}{60}\), \(\frac{36}{90}\)
Explanation:
The original ratio is 12/30. Shade the row for 12 and the row for 30 on the multiplication table.
The column for 2 shows there are 2 ∙ 12 when there are 2 ∙ 30. So, 12/30 equal to 24/60
The column for 3 shows there are 3 ∙ 12 when there are 3 ∙ 30. So, 12/30 equal to 36/90
Question 7.
\(\frac{2}{9}\)
Type below:
___________
Answer:
\(\frac{2}{9}\) = \(\frac{4}{18}\), \(\frac{6}{27}\)
Explanation:
The original ratio is 2/9. Shade the row for 2 and the row for 9 on the multiplication table.
The column for 2 shows there are 2 ∙ 2, when there are 2 ∙ 9. So, 2/9 equal to 4/18
The column for 3 shows there are 3 ∙ 2, when there are 3 ∙ 9. So, 2/9 equal to 6/27
On Your Own
Write two equivalent ratios.
Question 8.
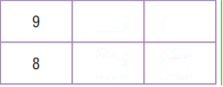
Type below:
___________
Answer:
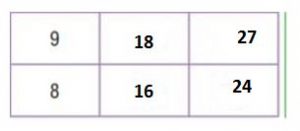
Explanation:
The original ratio is 9/8. Shade the row for 9 and the row for 8 on the multiplication table.
The column for 2 shows there are 2 ∙ 9 when there are 2 ∙ 8. So, 9/8 equal to 18/16
The column for 3 shows there are 3 ∙ 9 when there are 3 ∙ 8. So, 9/8 equal to 27/24
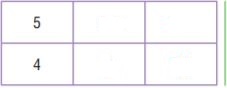
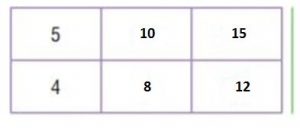
Question 9.
Type below:
___________
Answer:
Explanation:
The original ratio is 5/4. Shade the row for 5 and the row for 4 on the multiplication table.
The column for 2 shows there are 2 ∙ 5 when there are 2 ∙ 4. So, 5/4 equal to 10/8
The column for 3 shows there are 3 ∙ 5 when there are 3 ∙ 4. So, 5/4 equal to 15/20
Question 10.
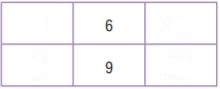
Type below:
___________
Answer:
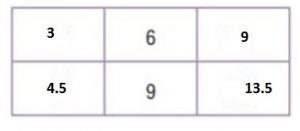
Explanation:
The original ratio is 6/9. Shade the row for 6 and the row for 9 on the multiplication table.
The column for 1 shows there are 1 ∙ 3 when there are 1. 4.5. So, 5/4 equal to 3/4.5
The column for 3 shows there are 3 ∙ 3 when there are 3 ∙ 4.5. So, 5/4 equal to 9/13.5
Question 11.
\(\frac{8}{7}\)
Type below:
___________
Answer:
\(\frac{8}{7}\) = \(\frac{16}{14}\), \(\frac{24}{21}\)
Explanation:
The original ratio is 8/7. Shade the row for 8 and the row for 7 on the multiplication table.
The column for 2 shows there are 2 ∙ 8, when there are 2 ∙ 7. So, 8/7 equal to 16/14
The column for 3 shows there are 3 ∙ 8, when there are 3 ∙ 7. So, 8/7 equal to 24/21
Question 12.
\(\frac{2}{6}\)
Type below:
___________
Answer:
\(\frac{2}{6}\) = \(\frac{4}{12}\), \(\frac{6}{18}\)
Explanation:
The original ratio is 2/6. Shade the row for 2 and the row for 6 on the multiplication table.
The column for 2 shows there are 2 ∙ 2, when there are 2 ∙ 6. So, 2/6 equal to 4/12
The column for 3 shows there are 3 ∙ 2, when there are 3 ∙ 6. So, 2/6 equal to 6/18
Question 13.
\(\frac{4}{11}\)
Type below:
___________
Answer:
\(\frac{4}{11}\) = \(\frac{8}{22}\), \(\frac{12}{33}\)
Explanation:
The original ratio is 4/11. Shade the row for 4 and the row for 11 on the multiplication table.
The column for 2 shows there are 2 ∙ 4, when there are 2 ∙ 11. So, 4/11 equal to 8/22
The column for 3 shows there are 3 ∙ 4, when there are 3 ∙ 11. So, 4/11 equal to 12/33
Determine whether the ratios are equivalent.
Question 14.
\(\frac{2}{3} \text { and } \frac{8}{12}\)
___________
Answer:
Yes
Explanation:
2/3 × 4/4 = 8/12
So, 2/3 is equal to 8/12
Question 15.
\(\frac{8}{10} \text { and } \frac{6}{10}\)
___________
Answer:
No
Explanation:
8/10 ÷ 2/2 = 4/5
8/10 is not equal to 6/10
Question 16.
\(\frac{16}{60} \text { and } \frac{4}{15}\)
___________
Answer:
yes
Explanation:
16/60 ÷ 4/4 = 4/15
16/60 is equal to 4/15
Question 17.
\(\frac{3}{14} \text { and } \frac{8}{28}\)
___________
Answer:
No
Explanation:
3/14 is not equal to 8/28
Problem Solving + Applications – Page No. 226
Use the multiplication table for 18 and 19.
Question 18.
In Keith’s baseball games this year, the ratio of times he has gotten on base to the times he has been at bat is \(\frac{4}{14}\). Write two ratios that are equivalent to \(\frac{4}{14}\).
Type below:
___________
Answer:
\(\frac{4}{14}\) = \(\frac{8}{28}\), \(\frac{2}{7}\)
Explanation:
4/14
multiply both numbers by 2
8/28
divide both numbers by 2
2/7
Question 19.
Pose a Problem Use the multiplication table to write a new problem involving equivalent ratios. Then solve the problem.
Type below:
___________
Answer:
The ratio of times he has gotten on base to the times he has been at bat is \(\frac{6}{9}\). Write two ratios that are equivalent to \(\frac{6}{9}\)
.multiply both numbers by 2 = 12/18
multiply both numbers by 3 = 18/ 27
Question 20.
Describe how to write an equivalent ratio for \(\frac{9}{27}\) without using a multiplication table.
Type below:
___________
Answer:
\(\frac{9}{27}\) = \(\frac{18}{54}\), \(\frac{3}{9}\)
Explanation:
\(\frac{9}{27}\)
multiply both numbers by 2, 18/54
divide both numbers by 3
3/9
Question 21.
Write a ratio that is equivalent to \(\frac{6}{9} \text { and } \frac{16}{24}\).
\(\frac{□}{□}\)
Answer:
\(\frac{2}{3}\)
Explanation:
\(\frac{6}{9} \text { and } \frac{16}{24}\)
\(\frac{2}{3}\) is the equivalent ratio to \(\frac{6}{9} \text { and } \frac{16}{24}\)
Question 22.
Determine whether each ratio is equivalent to \(\frac{1}{3}, \frac{5}{10}, \text { or } \frac{3}{5}\). Write the ratio in the correct box.

Type below:
___________
Answer:
3/9, 7/21, 18/30, 10/30
Explanation:
2/4 = 1/2
3/9 = 1/3
7/21 = 1/3
18/30 = 3/5
10/30 = 1/3
6/10 = 2/5
8/16 = 4/8 = 1/2
Equivalent Ratios and Multiplication Tables – Page No. 227
Write two equivalent ratios.
Question 1.
Use a multiplication table to write two ratios that are equivalent to \(\frac{5}{3}\).
Type below:
___________
Answer:
\(\frac{5}{3}\) = \(\frac{10}{6}\), \(\frac{15}{9}\)
Explanation:
The original ratio is 5/3. Shade the row for 5 and the row for 3 on the multiplication table.
The column for 2 shows there are 2 ∙ 5, when there are 2 ∙ 3. So, 5/3 equal to 10/6
The column for 3 shows there are 3 ∙ 5, when there are 3 ∙ 3. So, 5/3 equal to 15/9
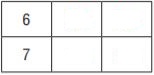
Question 2.
Type below:
___________
Answer:
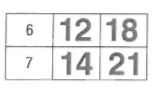
Explanation:
The original ratio is 6/7. Shade the row for 6 and the row for 7 on the multiplication table.
The column for 2 shows there are 2 ∙ 6 when there are 2 ∙ 7. So, 6/7 equal to 12/14
The column for 3 shows there are 3 ∙ 6 when there are 3 ∙ 7. So, 6/7 equal to 18/21
Question 2.
Type below:
___________
Answer:
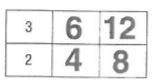
Explanation:
The original ratio is 3/2. Shade the row for 3 and the row for 2 on the multiplication table.
The column for 2 shows there are 2 ∙ 3 when there are 2 ∙ 2. So, 3/2 equal to 6/4
Multiply 3/2 with 4/4 = 12/8
Question 4.
\(\frac{6}{8}\)
Type below:
___________
Answer:
\(\frac{6}{8}\) =\(\frac{12}{16}\), \(\frac{18}{24}\)
Explanation:
The original ratio is 6/8. Shade the row for 6 and the row for 8 on the multiplication table.
The column for 2 shows there are 2 ∙ 6, when there are 2 ∙ 8. So, 6/8 equal to 12/16
The column for 3 shows there are 3 ∙ 6, when there are 3 ∙ 8. So, 6/8 equal to 18/24
Question 5.
\(\frac{11}{1}\)
Type below:
___________
Answer:
\(\frac{11}{1}\) = \(\frac{22}{2}\), \(\frac{33}{3}\)
Explanation:
The original ratio is 11/1. Shade the row for 11 and the row for 1 on the multiplication table.
The column for 2 shows there are 2 ∙ 11, when there are 2 ∙ 1. So, 11/1 equal to 22/2
The column for 3 shows there are 3 ∙ 11, when there are 3 ∙ 1. So, 11/1 equal to 33/3
Determine whether the ratios are equivalent.
Question 6.
\(\frac{2}{3} \text { and } \frac{5}{6}\).
___________
Answer:
No
Explanation:
2/3 is not equal to 5/6
Question 7.
\(\frac{5}{10} \text { and } \frac{1}{6}\).
___________
Answer:
No
Explanation:
5/10 is not equal to 1/6
Question 8.
\(\frac{8}{3} \text { and } \frac{32}{12}\).
___________
Answer:
Yes
Explanation:
8/3 × 4/4 = 32/12
8/3 is equal to 32/12
Question 9.
\(\frac{9}{12} \text { and } \frac{3}{4}\).
___________
Answer:
Yes
Explanation:
9/12 ÷ 3/3 = 3/4
9/12 is equal to 3/4
Problem Solving
Question 10.
Tristan uses 7 stars and 9 diamonds to make a design. Write two ratios that are equivalent to \(\frac{7}{9}\).
Type below:
___________
Answer:
\(\frac{7}{9}\) = \(\frac{14}{18}\) , \(\frac{21}{27}\)
Explanation:
Tristan uses 7 stars and 9 diamonds to make a design.
\(\frac{7}{9}\)
The original ratio is 7/9. Shade the row for 7 and the row for 9 on the multiplication table.
The column for 2 shows there are 2 ∙ 7, when there are 2 ∙ 9. So, 7/9 equal to 14/18
The column for 3 shows there are 3 ∙ 7, when there are 3 ∙ 9. So, 7/9 equal to 21/27
Question 12.
Explain how to determine whether two ratios are equivalent.
Type below:
___________
Answer:
If any ratio is multiplied or divided by the same number, then the ratios are equivalent.
Lesson Check – Page No. 228
Question 1.
A pancake recipe calls for 4 cups of flour and 3 cups milk. Does a recipe calling for 2 cups flour and 1.5 cups milk use the same ratio of flour to milk?
___________
Answer:
A muffin recipe that calls for 2 cups flour and 1.5 cups milk
Explanation:
A pancake recipe calls for 4 cups of flour and 3 cups milk. A muffin recipe that calls for 2 cups flour and 1.5 cups milk.
Question 2.
A bracelet is made of 14 red beads and 19 gold beads. A necklace is made of 84 red beads and 133 gold beads. Do the two pieces of jewelry have the same ratio of red beads to gold beads?
___________
Answer:
The bracelet has 14 red and 19 gold, so the ratio between red and gold is 14/19. We cannot simplify this ratio as there are not common factors between 14 and 19, because 19 is a prime number.
As there are 84 red and 133 gold the ratio will be 84/133. For this ratio to be equal to 14/19 it should be that 84 is multiple of 14 and 133 multiple of 19, and both multiples must the same,
84/133 is not equal to 14/19
Spiral Review

Question 5.
Delia has 3 \(\frac{5}{8}\) yards of ribbon. About how many \(\frac{1}{4}\)-yard-long pieces can she cut?
About _____ pieces
Answer:
About 14 pieces
Explanation:
Length of yards of ribbon is 3 5/8 = 29/8
Length of yards of ribbon pieces need to be cut is 1/4
Number of yards = 29/8 ÷ 1/4 = 14.5 = 14
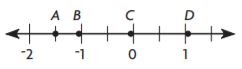
Question 6.
Which point is located at –1.1?
Type below:
___________
Answer:
B
Explanation:
-1.1 is in between -1 and -2
-1.1 is close to -1
So, the answer is point B
Share and Show – Page No. 231
Question 1.
In Jawan’s school, 4 out of 10 students chose basketball as a sport they like to watch, and 3 out of 5 students chose football. Is the ratio of students who chose basketball (4 to 10) equivalent to the ratio of students who chose football (3 to 5)?
Type below:
___________
Answer:
the ratio of students who chose basketball (4 to 10) is not equivalent to the ratio of students who chose football (3 to 5)
Explanation:
In Jawan’s school, 4 out of 10 students chose basketball as a sport they like to watch, and 3 out of 5 students chose football.
4/10 = 0.4
3/5 = 0.6
0.4 is not equal to 0.6
The ratio of students who chose basketball (4 to 10) is not equivalent to the ratio of students who chose football (3 to 5)

Question 3.
Look for Structure The table shows the results of the quizzes Hannah took in one week. Did Hannah get the same score on her math and science quizzes? Explain.
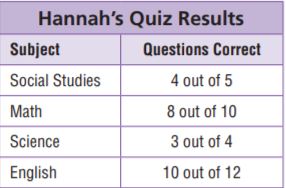
Type below:
___________
Answer:
Hannah didn’t get the same score on her math and science quizzes
Explanation:
Social Studies = 4/5
Math = 8/10 = 0.8
Science = 3/4 = 0.75
English = 10/12
Math = 8/10
Divide the 8/10 with 2/2 = 8/10 ÷ 2/2 = 4/5
Hannah didn’t get the same score on her math and science quizzes
Question 4.
Did Hannah get the same score on the quizzes in any of her classes? Explain.
Type below:
___________
Answer:
The ratio of Social Studies is equal to the ratio of Math
Explanation:
Social Studies = 4/5 = 0.8
Math = 8/10 = 0.8
Science = 3/4 = 0.75
English = 10/12 = 0.8333
The ratio of Social Studies is equal to the ratio of Math
On Your Own – Page No. 232

Question 6.
A florist offers three different bouquets of tulips and irises. The list shows the ratios of tulips to irises in each bouquet. Determine the bouquets that have equivalent ratios.

Type below:
___________
Answer:
The ratio of Spring Mix is equal to the ratio of Splash of Sun
Explanation:
Spring Mix = 4/6 = 0.66
Morning Melody = 9/12 = 0.75
Splash of Sun = 10/15 =0.66
The ratio of Spring Mix is equal to the ratio of Splash of Sun
Question 7.
The ratio of boys to girls in a school’s soccer club is 3 to 5. The ratio of boys to girls in the school’s chess club is 13 to 15. Is the ratio of boys to girls in the soccer club equivalent to the ratio of boys to girls in the chess club? Explain
Type below:
___________
Answer:
No
Explanation:
They are not equivalent because you can not reduce 13 any further because it is a prime number and if you multiply 3 by 3 and 5 by 3 you would get 9:15 as the equivalent ratio.
Question 8.
Analyze Thad, Joey, and Mia ran in a race. The finishing times were 4.56 minutes, 3.33 minutes, and 4.75 minutes. Thad did not finish last. Mia had the fastest time. What was each runner’s time?
Type below:
___________
Answer:
Mia = 3.33 minutes
Joey = 4.75 minutes
Thad = 4.56 minutes
Explanation:
Mia had the fastest time. 3.33 minutes
Thad did not finish last. So, Joey = 4.75 minutes
Thad = 4.56 minutes
Question 9.
Fernando donates $2 to a local charity organization for every $15 he earns. Cleo donates $4 for every $17 she earns. Is Fernando’s ratio of money donated to money earned equivalent to Cleo’s ratio of money donated to money earned? Explain.
Type below:
___________
Answer:
Fernando’s ratio of money donated to money earned is not equivalent to Cleo’s ratio of money donated to money earned
Explanation:
Fernando donates $2 to a local charity organization for every $15 he earns.
$2/$15 = 0.1333
Cleo donates $4 for every $17 she earns. $4/$17 = 0.2359
Fernando’s ratio of money donated to money earned is not equivalent to Cleo’s ratio of money donated to money earned
Problem Solving Use Tables to Compare Ratios – Page No. 233
Read each problem and solve.
Question 1.
Sarah asked some friends about their favorite colors. She found that 4 out of 6 people prefer blue, and 8 out of 12 people prefer green. Is the ratio of friends who chose blue to the total asked equivalent to the ratio of friends who chose green to the total asked?
Type below:
___________
Answer:
Yes, 4/6 is equivalent to 8/12
Explanation:

4/6 = 0.666
8/12 = 0.666
Question 2.
Lisa and Tim make necklaces. Lisa uses 5 red beads for every 3 yellow beads. Tim uses 9 red beads for every 6 yellow beads. Is the ratio of red beads to yellow beads in Lisa’s necklace equivalent to the ratio in Tim’s necklace?
Type below:
___________
Answer:
The ratio of red beads to yellow beads in Lisa’s necklace is not equivalent to the ratio in Tim’s necklace
Explanation:
Lisa and Tim make necklaces. Lisa uses 5 red beads for every 3 yellow beads.
5/3 = 1.666
Tim uses 9 red beads for every 6 yellow beads. 9/6 = 1.5
The ratio of red beads to yellow beads in Lisa’s necklace is not equivalent to the ratio in Tim’s necklace
Question 3.
Mitch scored 4 out of 5 on a quiz. Demetri scored 8 out of 10 on a quiz. Did Mitch and Demetri get equivalent scores?
Type below:
___________
Answer:
Mitch and Demetri get equivalent scores
Explanation:
Mitch scored 4 out of 5 on a quiz. 4/5 = 0.8
Demetri scored 8 out of 10 on a quiz. = 8/10 = 0.8
Mitch and Demetri get equivalent scores

Page No. 234
Question 1.
Mrs. Sahd distributes pencils and paper to students in the ratio of 2 pencils to 10 sheets of paper. Three of these ratios are equivalent to \(\frac{2}{10}\). Which one is NOT equivalent?
\(\frac{1}{5} \frac{7}{15} \frac{4}{20} \frac{8}{40}\)
Type below:
___________
Answer:
\(\frac{7}{15}\) is not equal \(\frac{2}{10}\)
Explanation:
Mrs. Sahd distributes pencils and paper to students in the ratio of 2 pencils to 10 sheets of paper. Three of these ratios are equivalent to \(\frac{2}{10}\) = 0.2
\(\frac{1}{5}\) = 0.2
\(\frac{7}{15}\) = 0.4666
\(\frac{4}{20}\) = 0.2
\(\frac{8}{40}\) = 0.2
\(\frac{7}{15}\) is not equal \(\frac{2}{10}\)
Question 2.
Keith uses 18 cherries and 3 peaches to make a pie filling. Lena uses an equivalent ratio of cherries to peaches when she makes pie filling. Can Lena use a ratio of 21 cherries to 6 peaches? Explain.
Type below:
___________
Answer:
No, she cannot use a ratio of 21 cherries to 6 peaches
Explanation:
Keith uses 18 cherries and 3 peaches to make a pie filling. 18/3 = 6
Lena uses a ratio of 21 cherries to 6 peaches, 21/6 = 3.5
No, she cannot use a ratio of 21 cherries to 6 peaches
Spiral Review
Question 3.
What is the quotient \(\frac{3}{20} \div \frac{7}{10}\)?
Type below:
___________
Answer:
\(\frac{3}{14}\)
Explanation:
\(\frac{3}{20} \div \frac{7}{10}\)
3/20 × 10/7 = 3/14

Question 5.
Alicia plots a point at (0, 5) and (0, –2). What is the distance between the points?
Type below:
___________
Answer:
7 units
Explanation:
Alicia plots a point at (0, 5) and (0, –2).
The given points have the same x-coordinates.
|-2| = 2
5 + 0 = 5
0 + 2 = 2
5 + 2 = 7
The distance is 7 units
Question 6.
Morton sees these stickers at a craft store. What is the ratio of clouds to suns?
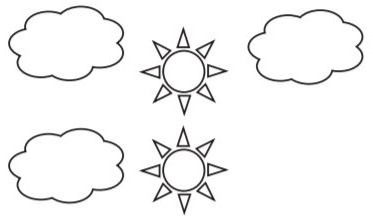
Type below:
___________
Answer:
3 : 2
Explanation:
there are 3 clouds and 2 suns. So, the ratio is 3 to 2.
Share and Show – Page No. 237
Use equivalent ratios to find the unknown value.
Question 1.
\(\frac{?}{10}=\frac{4}{5}\)
_____
Answer:
\(\frac{8}{10}\) = \(\frac{4}{5}\)
Explanation:
Use common denominators to write equivalent ratios.
10 is a multiple of 5, so 10 is a common denominator.
Multiply the 4 and denominator by 2 to write the ratios using a common denominator.
4/5 × 2/2 = 8/10
The denominators are the same, so the numerators are equal to each other.
So, the unknown value is 8/10 = 4/5
\(\frac{8}{10}\)
Question 2.
\(\frac{18}{24}=\frac{6}{?}\)
_____
Answer:
\(\frac{6}{8}\) = \(\frac{18}{24}\)
Explanation:
Write an equivalent ratio with 18 in the numerator.
Divide 18 by 6 to get 3
So, divide the denominator by 24 as well.
24/3 = 8
The numerators are the same, so the denominators are equal to each other.
So, the unknown value is 6/8 = 18/24
\(\frac{6}{8}\)

Question 4.
\(\frac{?}{5}=\frac{8}{10}\)
_____
Answer:
\(\frac{4}{5}\)
Explanation:
Write an equivalent ratio with 10 in the denominator.
Divide 10 by 2 to get 5
So, divide the numerator 8 as well.
8/2 = 4
The denominators are the same, so the numerators are equal to each other.
So, the unknown value is 8/10 = 4/5
\(\frac{4}{5}\)
Question 5.
\(\frac{7}{4}=\frac{?}{12}\)
_____
Answer:
\(\frac{21}{12}\)
Explanation:
Write an equivalent ratio with 12 in the denominator.
Multiply 4 with 3 to get 12
So, Multiply 7 with 3 to get the numerator of unknown number.
7 × 3 = 21
The denominators are the same, so the numerators are equal to each other.
So, the unknown value is 21/12 = 7/4
\(\frac{21}{12}\)
Question 6.
\(\frac{10}{?}=\frac{40}{12}\)
_____
Answer:
\(\frac{10}{3}\)
Explanation:
Write an equivalent ratio with 40 in the numerator.
Divide 40 by 4 to get 10
So, divide the denominator 12 as well.
12/4 = 3
The numerators are the same, so the denominators are equal to each other.
So, the unknown value is 10/3 = 40/12
\(\frac{10}{3}\)
On Your Own
Use equivalent ratios to find the unknown value.
Question 7.
\(\frac{2}{6}=\frac{?}{30}\)
_____
Answer:
\(\frac{10}{30}\)
Explanation:
Use common denominators to write equivalent ratios.
30 is a multiple of 6, so 30 is a common denominator.
Multiply the 6 and denominator by 5 to write the ratios using a common denominator.
2/6 × 5/5 =10/30
The denominators are the same, so the numerators are equal to each other.
So, the unknown value is 10/30 = 2/6
\(\frac{10}{30}\)
Question 8.
\(\frac{5}{?}=\frac{55}{110}\)
_____
Answer:
\(\frac{5}{10}\)
Explanation:
Write an equivalent ratio with 55 in the numerator.
Divide 55 with 11 to get 5
So, Divide 110 with 11 to get the denominator of unknown number.
110/11 = 10
The numerators are the same, so the denominators are equal to each other.
So, the unknown value is 5/10 = 55/110
\(\frac{5}{10}\)
Question 9.
\(\frac{3}{9}=\frac{9}{?}\)
_____
Answer:
\(\frac{9}{27}\)
Explanation:
Write an equivalent ratio with 9 in the numerator.
Multiply 3 with 3 to get 9
So, Multiply 9 with 3 to get the denominator of unknown number.
9 × 3 = 27
The numerators are the same, so the denominators are equal to each other.
So, the unknown value is 9/27 = 3/9
\(\frac{9}{27}\)
Question 10.
\(\frac{?}{6}=\frac{16}{24}\)
_____
Answer:
\(\frac{4}{6}\)
Explanation:
Use common denominators to write equivalent ratios.
Divide 24 with 4 to get 6.
So, divide 16 with 4 to know the unknown number of numerator
16/4 = 4
The denominators are the same, so the numerators are equal to each other.
So, the unknown value is 4/6 = 16/24
\(\frac{4}{6}\)
Question 12.
The ratio of boys to girls in a choir is 3 to 8. There are 32 girls in the choir. How many members are in the choir?
_____ members
Answer:
12 members
Explanation:
The ratio of boys to girls in a choir is 3 to 8.
3/8 × 4/ 4 = 12/32
So, if there are 32 girls in the choir, there will be 12 boys present.

Problem Solving + Applications – Page No. 238
Solve by finding an equivalent ratio.
Question 14.
It takes 8 minutes for Sue to make 2 laps around the go-kart track. How many laps can Sue completely in 24 minutes?
_____ laps
Answer:
6 laps
Explanation:
It takes 8 minutes for Sue to make 2 laps around the go-kart track.
For 24 minutes, (24 × 2)/8 = 48/8 =6
Question 15.
The width of Jay’s original photo is 8 inches. The length of the original photo is 10 inches. He prints a smaller version that has an equivalent ratio of width to length. The width of the smaller version is 4 inches less than the width of the original. What is the length of the smaller version?
_____ inches
Answer:
5 inches
Explanation:
The width of Jay’s original photo is 8 inches. The length of the original photo is 10 inches.
8/10
He prints a smaller version that has an equivalent ratio of width to length. The width of the smaller version is 4 inches less than the width of the original.
4/s
8/10 ÷ 2/2 = 4/5
5 inches
Question 17.
What’s the Error? Greg used the steps shown to find the unknown value. Describe his error and give the correct solution.
\(\frac{2}{6}=\frac{?}{12}\)
\(\frac{2+6}{6+6}=\frac{?}{12}\)
\(\frac{8}{12}=\frac{?}{12}\)
The unknown value is 8.
Type below:
___________
Answer:
Greg added 6 to the numerator and denominator which is not correct to find the unknown value.
\(\frac{2}{6}=\frac{?}{12}\)
2/6 × 2/2 = 4/12
4 is the unknown value.
Question 18.
Courtney bought 3 maps for $10. Use the table of equivalent ratios to find how many maps she can buy for $30.

Type below:
___________
Answer:
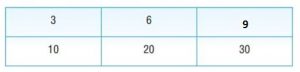
Explanation:
3/10 × 3/3 = 9/30
Use Equivalent Ratios – Page No. 239
Use equivalent ratios to find the unknown value.
Question 1.
\(\frac{4}{10}=\frac{?}{40}\)
_____
Answer:
\(\frac{16}{40}\)
Explanation:
4/10 × 4/4 = 16/40
Question 2.
\(\frac{3}{24}=\frac{33}{?}\)
_____
Answer:
\(\frac{33}{264}\)
Explanation:
3/24 × 11/11 = 33/264


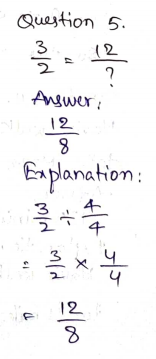
Question 6.
\(\frac{4}{5}=\frac{?}{40}\)
_____
Answer:
\(\frac{32}{40}\)
Explanation:
4/5 × 8/8 = 32/40
Question 7.
\(\frac{?}{2}=\frac{45}{30}\)
_____
Answer:
\(\frac{3}{2}\)
Explanation:
45/30 ÷ 15/15 = 3/2
Question 8.
\(\frac{45}{?}=\frac{5}{6}\)
_____
Answer:
\(\frac{45}{54}\)
Explanation:
5/6 × 9/9 = 45/54
Problem Solving
Question 9.
Honeybees produce 7 pounds of honey for every 1 pound of beeswax they produce. Use equivalent ratios to find how many pounds of honey are produced when 25 pounds of beeswax are produced.
_____ pounds
Answer:
175 pounds
Explanation:
Honeybees produce 7 pounds of honey for every 1 pound of beeswax they produce.
7/1
25 pounds of beeswax, 25 × 7 = 175 pounds
Question 10.
A 3-ounce serving of tuna provides 21 grams of protein. Use equivalent ratios to find how many grams of protein are in 9 ounces of tuna.
_____ grams of protein
Answer:
63 grams of protein
Explanation:
A 3-ounce serving of tuna provides 21 grams of protein.
For 9 ounces of tuna, (21 × 9)/3 = 63
Question 11.
Explain how using equivalent ratios is like adding fractions with unlike denominators.
Type below:
___________
Answer:
Equivalent ratios have different numbers but represent the same relationship. In this tutorial, you’ll see how to find equivalent ratios by first writing the given ratio as a fraction. And it cannot be the same by adding two fraction with different ratio
Lesson Check – Page No. 240

Question 2.
A certain shade of orange paint is made by mixing 3 quarts of red paint with 2 quarts of yellow paint. To make more paint of the same shade, how many quarts of yellow paint should be mixed with 6 quarts of red paint?
_____ quarts
Answer:
4 quarts
Explanation:
A certain shade of orange paint is made by mixing 3 quarts of red paint with 2 quarts of yellow paint.
3 quarts of red paint is mixed with 2 quarts of yellow paint
So, 6 quarts of red paint is mixed with 6/3 × 2 = 4 quarts of yellow paint
Spiral Review
Question 3.
What is the quotient \(2 \frac{4}{5} \div 1 \frac{1}{3}\)?
______ \(\frac{□}{□}\)
Answer:
2\(\frac{1}{10}\)
Explanation:
2 4/5 = 14/5 = 2.8
1 1/3 = 4/3 = 1.333
2.8/1.333 = 2 1/10
Question 4.
What is the quotient \(-2 \frac{2}{3}\)?
______ \(\frac{□}{□}\)
Answer:
1\(\frac{11}{16}\)
Explanation:
−4 1/2 ÷ -2 2/3
1 11/16

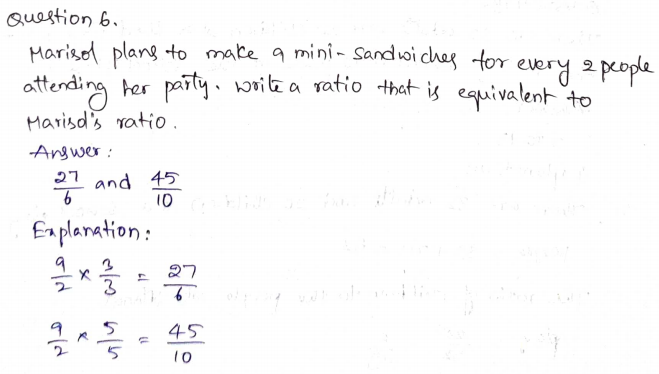
Mid-Chapter Checkpoint – Vocabulary – Page No. 241
Choose the best term from the box to complete the sentence.

Question 1.
A _____ is a rate that makes a comparison to 1 unit.
Type below:
___________
Answer:
rate
Question 2.
Two ratios that name the same comparison are _____ .
Type below:
___________
Answer:
Equivalent Ratios
Concepts and Skills

Question 3.
Write the ratio of red circles to blue squares.
Type below:
___________
Answer:
3 : 5
Explanation:
There are 3 red counter and 5 square boxes.
So, the ratio is 3 : 5
Write the ratio in two different ways.
Question 4.
8 to 12
Type below:
___________
Answer:
\(\frac{8}{12}\)
8 : 12
Explanation:
8 to 12 as a fraction \(\frac{8}{12}\)
8 to 12 with a colon 8 : 12
Question 5.
7 : 2
Type below:
___________
Answer:
\(\frac{7}{2}\)
7 to 2
Explanation:
7 : 2 as a fraction \(\frac{7}{2}\)
7 : 2 using words 7 to 2
Question 6.
\(\frac{5}{9}\)
Type below:
___________
Answer:
5 to 9
5 : 9
Explanation:
\(\frac{5}{9}\) using words 5 to 9
\(\frac{5}{9}\) with a colon 5 : 9
Question 7.
11 to 3
Type below:
___________
Answer:
\(\frac{11}{3}\)
11 : 3
Explanation:
11 to 3 as a fraction \(\frac{11}{3}\)
11 to 3 with a colon 11 : 3
Write two equivalent ratios.
Question 8.
\(\frac{2}{7}\)
Type below:
___________
Answer:
\(\frac{2}{7}\) = \(\frac{4}{14}\), \(\frac{6}{21}\)
Explanation:
The original ratio is 2/7. Shade the row for 2 and the row for 7 on the multiplication table.
The column for 2 shows there are 2 ∙ 2, when there are 2 ∙ 7. So, 2/7 equal to 4/14
The column for 3 shows there are 3 ∙ 2, when there are 3 ∙ 7. So, 2/7 equal to 6/21
Question 9.
\(\frac{6}{5}\)
Type below:
___________
Answer:
\(\frac{6}{5}\) = \(\frac{12}{10}\), \(\frac{18}{15}\)
Explanation:
The original ratio is 6/5. Shade the row for 6 and the row for 5 on the multiplication table.
The column for 2 shows there are 2 ∙ 6, when there are 2 ∙ 5. So, 6/5 equal to 12/10
The column for 3 shows there are 3 ∙ 6, when there are 3 ∙ 5. So, 6/5 equal to 18/15
Question 10.
\(\frac{9}{12}\)
Type below:
___________
Answer:
\(\frac{9}{12}\) = \(\frac{18}{24}\), \(\frac{27}{36}\)
Explanation:
The original ratio is 9/12. Shade the row for 9 and the row for 12 on the multiplication table.
The column for 2 shows there are 2 ∙ 9, when there are 2 ∙ 12. So, 9/12 equal to 18/24
The column for 3 shows there are 3 ∙ 9, when there are 3 ∙ 12. So, 9/12 equal to 27/36
Question 11.
\(\frac{18}{6}\)
Type below:
___________
Answer:
\(\frac{18}{6}\) = \(\frac{36}{12}\), \(\frac{54}{18}\)
Explanation:
The original ratio is 18/6. Shade the row for 18 and the row for 6 on the multiplication table.
The column for 2 shows there are 2 ∙ 18, when there are 2 ∙ 6. So, 18/6 equal to 36/12
The column for 3 shows there are 3 ∙ 18, when there are 3 ∙ 6. So, 18/6 equal to 54/18
Find the unknown value.


Question 14.
\(\frac{48}{16}=\frac{?}{8}\)
Type below:
___________
Answer:
24
Explanation:
48/16 ÷ 2/2 = 24/8
So, the unknown number is 24
Question 15.
\(\frac{9}{36}=\frac{3}{?}\)
Type below:
___________
Answer:
12
Explanation:
9/36 ÷ 3/3 = 3/12
So, the unknown number is 12
Page No. 242
Question 16.
There are 36 students in the chess club, 40 students in the drama club, and 24 students in the film club. What is the ratio of students in the drama club to students in the film club?
Type below:
___________
Answer:
40 to 24
Explanation:
There are 36 students in the chess club, 40 students in the drama club, and 24 students in the film club.
The ratio of students in the drama club to students in the film club 40 to 24
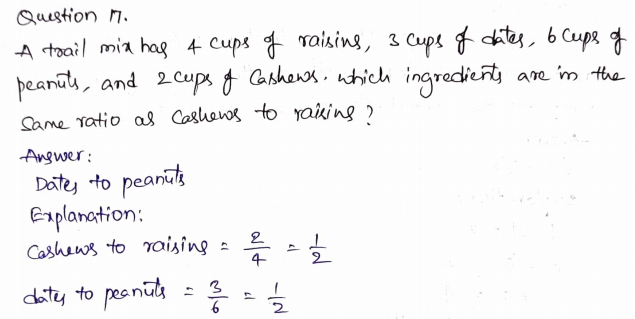

Question 19.
Sonya got 8 out of 10 questions right on a quiz. She got the same score on a quiz that had 20 questions. How many questions did Sonya get right on the second quiz? How many questions did she get wrong on the second quiz?
Type below:
___________
Answer:
4 wrong
Explanation:
8/10 = x/20
So, 10 × 2 = 20, so 8 × 2=16
so she got 16 out of 20 right and 20 – 16 = 4
She got 4 wrong.
Share and Show – Page No. 245
Write the rate as a fraction. Then find the unit rate.
Question 1.
Sara drove 72 miles on 4 gallons of gas.
_____ miles/gallon
Answer:
18 miles/gallon
Explanation:
Sara drove 72 miles on 4 gallons of gas.
72/4
Divide 72/4 with 4/4
72/4 ÷ 4/4 = 18
Question 2.
Dean paid $27.00 for 4 movie tickets.
$ _____ per ticket
Answer:
$6.75 per ticket
Explanation:
Dean paid $27.00 for 4 movie tickets.
$27.00/4
Divide $27.00/4 with 4/4
$27.00/4 ÷ 4/4 = $6.75


On Your Own
Write the rate as a fraction. Then find the unit rate.
Question 5.
A company packed 108 items in 12 boxes.
Type below:
___________
Answer:
9
Explanation:
A company packed 108 items in 12 boxes.
108/12
Divide 108/12 with 12/12
108/12 ÷ 12/12 = 9
Question 6.
There are 112 students for 14 teachers.
Type below:
___________
Answer:
8
Explanation:
There are 112 students for 14 teachers.
112/14
Divide 112/14 with 14/14
112/14 ÷ 14/14 = 8
Question 7.
Geoff charges $27 for 3 hours of swimming lessons. Anne charges $31 for 4 hours. How much more does Geoff charge per hour than Anne?
$ _____
Answer:
$1.25
Explanation:
Geoff charges $27 for 3 hours of swimming lessons.
$27/3 = $9 for an hour
Anne charges $31 for 4 hours.
$31/4 = $7.75
$9 – $7.75 = $1.25
Geoff charge $1.25 per hour more than Anne
Question 8.
Compare One florist made 16 bouquets in 5 hours. A second florist made 40 bouquets in 12 hours. Which florist makes bouquets at a faster rate?
Type below:
___________
Answer:
A second florist made 40 bouquets in 12 hours at a faster rate
Explanation:
Compare One florist made 16 bouquets in 5 hours.
16/5 = 3.2
A second florist made 40 bouquets in 12 hours.
40/12 = 3.333
A second florist made 40 bouquets in 12 hours at a faster rate
Tell which rate is faster by comparing unit rates.
Question 9.
\(\frac{160 \mathrm{mi}}{2 \mathrm{hr}} \text { and } \frac{210 \mathrm{mi}}{3 \mathrm{hr}}\)
Type below:
___________
Answer:
160mi/2hr
Explanation:
160mi/2hr ÷ 2/2 = 80mi/hr
210mi/3hr = 70mi/hr
80mi/hr > 70mi/hr
Question 10.
\(\frac{270 \mathrm{ft}}{9 \mathrm{min}} \text { and } \frac{180 \mathrm{ft}}{9 \mathrm{min}}\)
Type below:
___________
Answer:
270ft/9min
Explanation:
270ft/9min = 30ft/min
180ft/9min = 20ft/min
30ft/min > 20ft/min
Question 11.
\(\frac{250 \mathrm{m}}{10 \mathrm{s}} \text { and } \frac{120 \mathrm{m}}{4 \mathrm{s}}\)
Type below:
___________
Answer:
250m/10s
Explanation:
250m/10s = 25m/s
120m/4s = 20m/s
25m/s > 20m/s
Unlock the Problem – Page No. 246
Question 12.
Ryan wants to buy treats for his puppy. If Ryan wants to buy the treats that cost the least per pack, which treat should he buy? Explain.
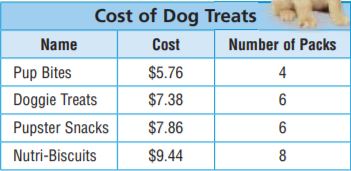
a. What do you need to find?
Type below:
___________
Answer:
We need to find that cost the least per pack
Question 12.
b. Find the price per pack for each treat.
Type below:
___________
Answer:
Pup bites = $5.76/4 ÷ 4/4 = $1.44
Doggie Treats = $7.38/6 ÷ 6/6 = $1.23
Pupster snacks = $7.86/6 ÷ 6/6 = $1.31
Nutri-Biscuits = $9.44/8 ÷ 8/8 = $1.18
Question 12.
c. Complete the sentences
The treat with the highest price per pack is _____.
The treat with the lowest price per pack is _____.
Ryan should buy _____ because _____.
Type below:
___________
Answer:
The treat with the highest price per pack is Pup bites.
The treat with the lowest price per pack is Nutri-Biscuits.
Ryan should buy Nutri-Biscuits because it has the least cost.
Question 13.
Reason Abstractly What information do you need to consider in order to decide whether one product is a better deal than another? When might the lower unit rate not be the best choice? Explain.
Type below:
___________
Answer:
We will consider the low cost in order to decide whether one product is a better deal than another.
The lower unit rate is not the best choice. Because it will show the highest cost.
Question 14.
Select the cars that get a higher mileage per gallon of gas than a car that gets 25 miles per gallon. Mark all that apply.
Options:
a. Car A 22 miles per 1 gallon
b. Car B 56 miles per 2 gallons
c. Car C 81 miles per 3 gallons
d. Car D 51 miles per 3 gallons
Answer:
b. Car B 56 miles per 2 gallons
c. Car C 81 miles per 3 gallons
Explanation:
22/1 = 22
56/2 = 28
81/3 = 27
51/3 = 17
Find Unit Rates – Page No. 247
Write the rate as a fraction. Then find the unit rate.
Question 1.
A wheel rotates through 1,800º in 5 revolutions.
Type below:
___________
Answer:
Explanation:
A wheel rotates through 1,800º in 5 revolutions.
1,800º/5 revolutions
1,800º/5 revolutions ÷ 5/5 = 360º/1revolution



Compare unit rates.
Question 5.
An online game company offers a package that includes 2 games for $11.98. They also offer a package that includes 5 games for $24.95. Which package is a better deal?
_____ package
Answer:
5 game package
Explanation:
An online game company offers a package that includes 2 games for $11.98.
$11.98/2 = $5.99
They also offer a package that includes 5 games for $24.95.
$24.95/5 = $4.99
Question 6.
At a track meet, Samma finished the 200-meter race in 25.98 seconds. Tom finished the 100-meter race in 12.54 seconds. Which runner ran at a faster average rate?
___________
Answer:
Tom
Explanation:
At a track meet, Samma finished the 200-meter race in 25.98 seconds.
200/25.98 seconds = 7.698 – meter/1 sec
Tom finished the 100-meter race in 12.54 seconds.
100 – meter/12.54 seconds = 7.974 – meter/1 sec
Problem Solving

Question 8.
Rachel bought 2 pounds of apples and 3 pounds of peaches for a total of $10.45. The apples and peaches cost the same amount per pound. What was the unit rate?
Type below:
___________
Answer:
$2.09 per pound
Explanation:
Rachel bought 2 pounds of apples and 3 pounds of peaches for a total of $10.45.
The apples and peaches cost the same amount per pound.
2 + 3 = 5
$10.45/5 = $2.09 per pound
Question 9.
Write a word problem that involves comparing unit rates.
Type below:
___________
Answer:
At a track meet, Samma finished the 200-meter race in 25.98 seconds. Tom finished the 100-meter race in 12.54 seconds. Which runner ran at a faster average rate?
At a track meet, Samma finished the 200-meter race in 25.98 seconds.
200/25.98 seconds = 7.698 – meter/1 sec
Tom finished the 100-meter race in 12.54 seconds.
100 – meter/12.54 seconds = 7.974 – meter/1 sec
Tom
Lesson Check – Page No. 248
Question 1.
Cran–Soy trail mix costs $2.99 for 5 ounces, Raisin–Nuts mix costs $3.41 for 7 ounces, Lots of Cashews mix costs $7.04 for 8 ounces, and Nuts for You mix costs $2.40 for 6 ounces. List the trail mix brands in order from the least expensive to the most expensive.
Type below:
___________
Answer:
Nuts for You, Raisin–Nuts, Cran–Soy trail mix, Lots of Cashews mix
Explanation:
Cran–Soy trail mix costs $2.99 for 5 ounces,
$2.99/5 = $0.598
Raisin–Nuts mix costs $3.41 for 7 ounces,
$3.41/7 = $0.487
Lots of Cashews mix costs $7.04 for 8 ounces,
$7.04/8 = $0.88
and Nuts for You mix costs $2.40 for 6 ounces.
$2.40/6 = $0.4
Question 2.
Aaron’s heart beats 166 times in 120 seconds. Callie’s heart beats 88 times in 60 seconds. Emma’s heart beats 48 times in 30 seconds. Galen’s heart beats 22 times in 15 seconds. Which two students’ heart rates are equivalent?
Type below:
___________
Answer:
Callie and Galen
Explanation:
Aaron’s heart beats 166 times in 120 seconds.
166/120 = 1.3833
Callie’s heart beats 88 times in 60 seconds.
88/60 = 1.4666
Emma’s heart beats 48 times in 30 seconds.
48/30 = 1.6
Galen’s heart beats 22 times in 15 seconds.
22/15 = 1.4666
Spiral Review

Question 4.
Write a comparison using < or > to show the relationship between |-\(\frac{2}{3}\)| and – \(\frac{5}{6}\).
Type below:
___________
Answer:
>
Explanation:
|-\(\frac{2}{3}\)| = 2/3 = 0.666
– \(\frac{5}{6}\) = -0.8333
|-\(\frac{2}{3}\)| > – \(\frac{5}{6}\)

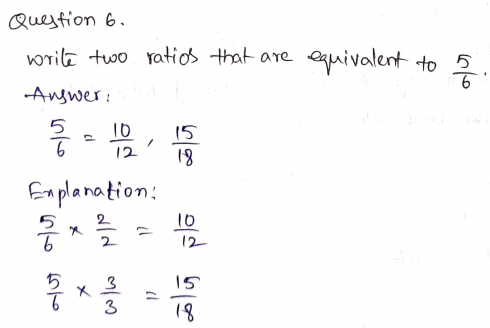
Share and Show – Page No. 251
Use a unit rate to find the unknown value.
Question 1.
\(\frac{10}{?}=\frac{6}{3}\)
_____
Answer:
5
Explanation:
6/3 ÷ 3/3 = 2/1
2/1 × 5/5 = 10/1
The unknown value is 5
Question 2.
\(\frac{6}{8}=\frac{?}{20}\)
_____
Answer:
15
Explanation:
6/8 ÷ 8/8 = 0.75/1
0.75/1 × 20/20 = 15/20
The unknown value is 15
On Your Own
Use a unit rate to find the unknown value.
Question 3.
\(\frac{40}{8}=\frac{45}{?}\)
_____
Answer:
9
Explanation:
40/8 ÷ 8/8 = 5/1
5/1 × 9/9 = 45/9
The unknown value is 9
Question 4.
\(\frac{42}{14}=\frac{?}{5}\)
_____
Answer:
15
Explanation:
42/14 ÷ 14/14 = 3/1
3/1 × 5/5 = 15/5
The unknown value is 15
Question 5.
\(\frac{?}{2}=\frac{56}{8}\)
_____
Answer:
14
Explanation:
56/8 ÷ 8/8 = 7/1
7/1 × 2/2 = 14/2
The unknown value is 14
Question 6.
\(\frac{?}{4}=\frac{26}{13}\)
_____
Answer:
8
Explanation:
26/13 ÷ 13/13 = 2/1
2/1 × 4/4 = 8/4
The unknown value is 8
Practice: Copy and Solve Draw a bar model to find the unknown value.
Question 7.
\(\frac{4}{32}=\frac{9}{?}\)
_____
Answer:

Explanation:
4/32 ÷ 32/32 = 0.125/1
0.125/1 × 72/72 = 9/72
The unknown value is 72
Question 8.
\(\frac{9}{3}=\frac{?}{4}\)
_____
Answer:
12
Explanation:
9/3 ÷ 3/3 = 3/1
3/1 × 4/4 = 12/4
The unknown value is 12
Question 9.
\(\frac{?}{14}=\frac{9}{7}\)
_____
Answer:
Explanation:
9/7 ÷ 7/7 = 1.2857/1
1.2857/1 × 14/14 = 18/14
The unknown value is 18
Question 10.
\(\frac{3}{?}=\frac{2}{1.25}\)
_____
Answer:
1.875
Explanation:
2/1.25 ÷ 1.25/1.25 = 1.6/1
1.6/1 × 1.875/1.875 = 3/1.875
The unknown value is 1.875
Question 11.
Communicate Explain how to find an unknown value in a ratio by using a unit rate.
Type below:
___________
Answer:
Firstly, Identify the known ratio, where both values are known. Then, Identify the ratio with one known value and one unknown value. Next, Use the two ratios to create a proportion. Finally, Cross-multiply to solve the problem.
Question 12.
Savannah is tiling her kitchen floor. She bought 8 cases of tile for $192. She realizes she bought too much tile and returns 2 unopened cases to the store. What was her final cost for tile?
$ _____
Answer:
$144
Explanation:
Savannah is tiling her kitchen floor. She bought 8 cases of tile for $192.
$192/8 ÷ 8/8 = $24 per each case of tile
She realizes she bought too much tile and returns 2 unopened cases to the store.
So, she bought 8 – 2 = 6 cases of tiles.
6 × $24 = $144
Problem Solving + Applications – Page No. 251
Pose a Problem
Question 13.
Josie runs a T-shirt printing company. The table shows the length and width of four sizes of T-shirts. The measurements of each size T-shirt form equivalent ratios.
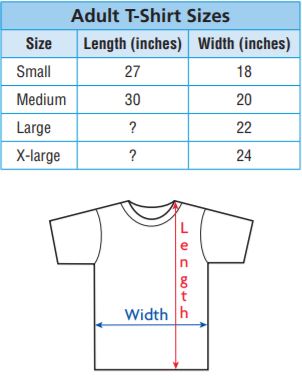
What is the length of an extra-large T-shirt?
Write two equivalent ratios and find the unknown value:
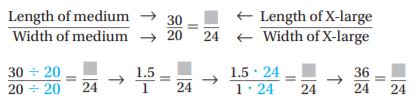
The length of an extra-large T-shirt is 36 inches.
Write a problem that can be solved by using the information in the table and could be solved by using equivalent ratios
Type below:
___________
Answer:
Small = 27/18 ÷ 18/18 = 1.5
Medium = 30/20 = 3/2 = 1.5
Large = 1.5/1 × 22/22 = 33/22
the length of an extra-large T-shirt = 1.5/1 × 24/24 = 36/24
What is the length of an large T-shirt?
Write two equivalent ratios and find the unknown value?
Large = 1.5/1 × 22/22 = 33/22
33/22 × 2/2 = 66/44
33/22 × 3/3 = 99/66
Question 14.
Peri earned $27 for walking her neighbor’s dog 3 times. If Peri earned $36, how many times did she walk her neighbor’s dog? Use a unit rate to find the unknown value.
_____ times
Answer:
4 times
Explanation:
Peri earned $27 for walking her neighbor’s dog 3 times.
If Peri earned $36, ($36 × 3)/$27 = 4
Use Unit Rates – Page No. 253
Use a unit rate to find the unknown value.
Question 1.
\(\frac{34}{7}=\frac{?}{7}\)
_____
Answer:
34
Explanation:
34/7 ÷ 7/7 = 4.8571/1
4.8571/1 × 7/7 = 34
The unknown value is 34
Question 2.
\(\frac{16}{32}=\frac{?}{14}\)
_____
Answer:
7
Explanation:
16/32 ÷ 32/32 = 0.5/1
0.5/1 × 14/14 = 7/1
The unknown value is 7
Question 3.
\(\frac{18}{?}=\frac{21}{7}\)
_____
Answer:
6
Explanation:
21/7 ÷ 7/7 = 3/1
3/1 × 6/6 = 18/6
The unknown value is 6
Question 4.
\(\frac{?}{16}=\frac{3}{12}\)
_____
Answer:
4
Explanation:
3/12 ÷ 12/12 = 0.25/1
0.25/1 × 16/16 = 4
The unknown value is 4
Draw a bar model to find the unknown value.
Question 5.
\(\frac{15}{45}=\frac{6}{?}\)
_____
Answer:
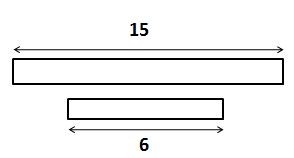
18
Explanation:
15/45 ÷ 45/45 = 1/3
1/3 × 6/6 = 6/18
The unknown value is 18
Question 6.
\(\frac{3}{6}=\frac{?}{7}\)
_____
Answer:
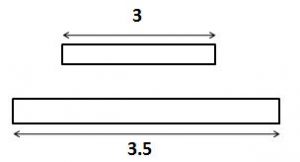
3.5
Explanation:
3/6 ÷ 6/6 = 1/2
1/2 × 3.5/3.5 = 3.5/7
The unknown value is 3.5
Problem Solving
Question 7.
To stay properly hydrated, a person should drink 32 fluid ounces of water for every 60 minutes of exercise. How much water should Damon drink if he rides his bike for 135 minutes?
_____ fluid ounces
Answer:
72 fluid ounces
Explanation:
To stay properly hydrated, a person should drink 32 fluid ounces of water for every 60 minutes of exercise.
If he rides his bike for 135 minutes, (135 × 32)/60 = 72
Question 8.
Lillianne made 6 out of every 10 baskets she attempted during basketball practice. If she attempted to make 25 baskets, how many did she make?
_____ baskets
Answer:
15 baskets
Explanation:
Lillianne made 6 out of every 10 baskets she attempted during basketball practice. If she attempted to make 25 baskets,
(25 × 6)/10 = 15 baskets
Question 9.
Give some examples of real-life situations in which you could use unit rates to solve an equivalent ratio problem.
Type below:
___________
Answer:
1) If a 10-ounce box of cereal costs $3 and a 20-ounce box of cereal costs $5, the 20-ounce box is the better value because each ounce of cereal is cheaper.
2) Yoda Soda is the intergalactic party drink that will have all your friends saying, “Mmmmmm, good this is!”
You are throwing a party, and you need 555 liters of Yoda Soda for every 121212 guests.
If you have 363636 guests, how many liters of Yoda Soda do you need?
Lesson Check – Page No. 254

Question 2.
Landry’s neighbor pledged $5.00 for every 2 miles he swims in a charity swim-a-thon. If Landry swims 3 miles, how much money will his neighbor donate?
$ _____
Answer:
$7.5
Explanation:
Landry’s neighbor pledged $5.00 for every 2 miles he swims in a charity swim-a-thon. If Landry swims 3 miles, 15/2 = $7.5
Spiral Review
Question 3.
Describe a situation that could be represented by –8.
Type below:
___________
Answer:
In Alaska the normal temperature in December was 3 degrees. Scientist predicted that by February the temperature would drop 11 degrees. What is the predicted temperature for February? The answer is -8.
Question 4.
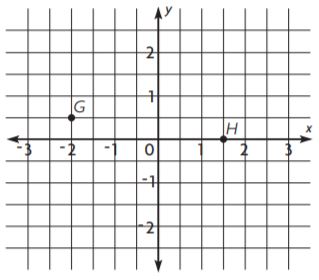
What are the coordinates of point G?
Type below:
___________
Answer:
(-2, 0.5)
Explanation:
The x-coordinate is -2
The y-coordinate is 0.5


Share and Show – Page No. 257
A redwood tree grew at a rate of 4 feet per year. Use this information for 1–3.
Question 1.
Complete the table of equivalent ratios for the first 5 years.
Type below:
___________
Answer:
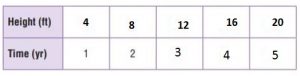
Explanation:
A redwood tree grew at a rate of 4 feet per year.
For 2 years, 2 × 4 = 8ft
For 3 years, 3 × 4 = 12ft
For 4 years, 4 × 4 = 16ft
For 5 years, 5 × 4 = 20ft
Question 2.
Write ordered pairs, letting the x-coordinate represent time in years and the y-coordinate represent height in feet.
Type below:
___________
Answer:
(1, 4), (2, 8), (3, 12), (4, 16), (5, 20)
Question 3.
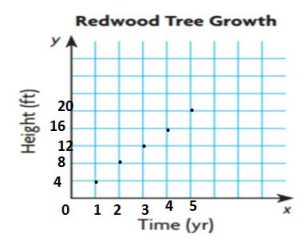
Use the ordered pairs to graph the tree’s growth over time.
Type below:
___________
Answer:
On Your Own
The graph shows the rate at which Luis’s car uses gas, in miles per gallon. Use the graph for 4–8.
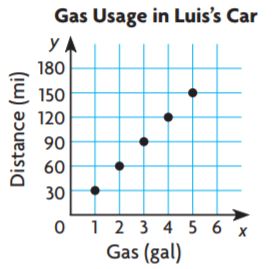
Question 4.
Complete the table of equivalent ratios.
Type below:
___________
Answer:
30/1, 60/2, 90/3, 120/4, 150/5
Question 5.
Find the car’s unit rate of gas usage.
Type below:
___________
Answer:
30mi/gal
Question 6.
How far can the car go on 5 gallons of gas?
_____ miles
Answer:
150 miles
Explanation:
the car go on 5 gallons of gas, 150/5
Question 7.
Estimate the amount of gas needed to travel 50 miles.
Type below:
___________
Answer:
5/3
Explanation:
30/1,
50/30 = 5/3
Question 8.
Ellen’s car averages 35 miles per gallon of gas. If you used equivalent ratios to graph her car’s gas usage, how would the graph differ from the graph of Luis’s car’s gas usage?
Type below:
___________
Answer:
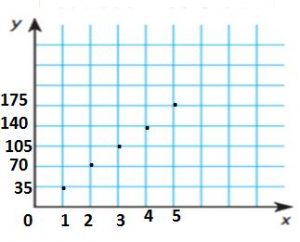
The distance is high for Ellen’s car’s gas usage compared to Luis’s car’s gas usage per one gal
Explanation:
35/1 × 2/2 = 70/2
35/1 × 3/3 = 105/3
35/1 × 4/4 = 140/4
35/1 × 5/5 = 175/5
Problem Solving + Applications – Page No. 258
Question 9.
Look for Structure The graph shows the depth of a submarine over time. Use equivalent ratios to find the number of minutes it will take the submarine to descend 1,600 feet.
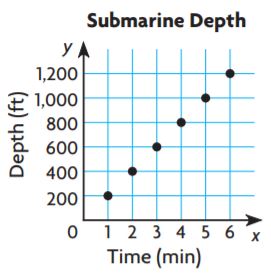
_____ minutes
Answer:
8 minutes
Explanation:
200/1 × 8/8 = 1600/8
Question 10.
The graph shows the distance that a plane flying at a steady rate travels over time. Use equivalent ratios to find how far the plane travels in 13 minutes.
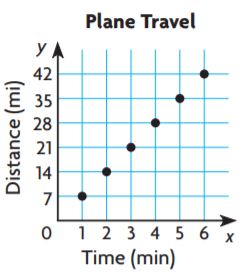
_____ miles
Answer:
91 miles
Explanation:
7/1 × 13/13 = 91/13
Question 11.
Sense or Nonsense? Emilio types at a rate of 84 words per minute. He claims that he can type a 500-word essay in 5 minutes. Is Emilio’s claim sense or nonsense? Use a graph to help explain your answer.
Type below:
___________
Answer:
He said that he can write 84 in 60sec ,500 words will be written in 500×60/84=357 it’s a nonsense
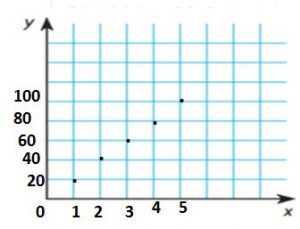
Question 12.
The Tuckers drive at a rate of 20 miles per hour through the mountains. Use the ordered pairs to graph the distance traveled over time.
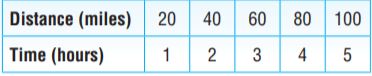
Type below:
___________
Answer:
Equivalent Ratios and Graphs – Page No. 259
Christie makes bracelets. She uses 8 charms for each bracelet. Use this information for 1–3.
Question 1.
Complete the table of equivalent ratios for the first 5 bracelets.
Type below:
___________
Answer:
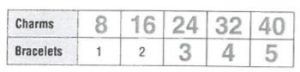
Explanation:
Question 2.
Write ordered pairs, letting the x-coordinate represent the number of bracelets and the y-coordinate represents the number of charms.
Type below:
___________
Answer:
(1, 8), (2, 16), (3, 24), (4, 32), (5, 40)
Question 3.
Use the ordered pairs to graph the charms and bracelets.
Type below:
___________
Answer:
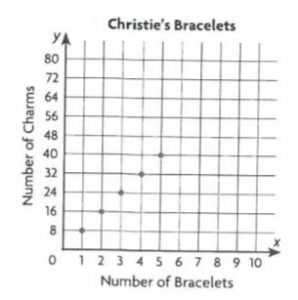
The graph shows the number of granola bars that are in various numbers of boxes of Crunch N Go. Use the graph for 4–5.
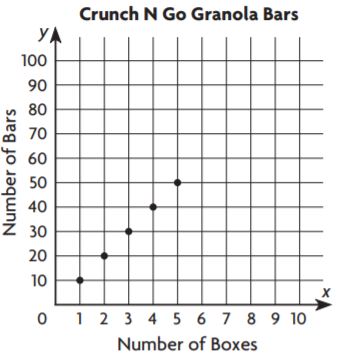
Question 4.
Complete the table of equivalent ratios.

Type below:
___________
Answer:

Question 5.
Find the unit rate of granola bars per box.
Type below:
___________
Answer:
10 bars/1 box
Problem Solving
Question 6.
Look at the graph for Christie’s Bracelets. How many charms are needed for 7 bracelets?
_____ charms
Answer:
56 charms
Question 7.
Look at the graph for Crunch N Go Granola Bars. Stefan needs to buy 90 granola bars. How many boxes must he buy?
_____ boxes
Answer:
9 boxes
Question 8.
Choose a real-life example of a unit rate. Draw a graph of the unit rate. Then explain how another person could use the graph to find the unit rate.
Type below:
___________
Answer:
Sam prepares 4 bracelets per month. How many bracelets does she prepare in a span of 6 months?
For 1 month, 1 × 4 = 4 bracelets
For 2 months, 2 × 4 = 8 bracelets
For 3 months, 3 × 4 = 12 bracelets
For 4 months, 4 × 4 = 16 bracelets
For 5 months, 5 × 4 = 20 bracelets
Lesson Check – Page No. 260

Question 2.
Maura charges $11 per hour to babysit. She makes a graph comparing the amount she charges (the y-coordinate) to the time she babysits (the x-coordinate). Which ordered pair shown is NOT on the graph?
(4, 44) (11, 1) (1, 11) (11, 12)
Type below:
___________
Answer:
(11, 1)
Explanation:
It is not 11,1 because she charges 11 hours per hour (y coordinate) and x would be time to babysit. so it can’t be 11,1
Spiral Review
Question 3.
List 0, –4, and 3 from least to greatest.
Type below:
___________
Answer:
-4, 0, 3
Question 4.
What two numbers can be used in place of the ? to make the statement true?
|?| = \(\frac{8}{9}\)
Type below:
___________
Answer:
–\(\frac{8}{9}\), \(\frac{8}{9}\)
Explanation:
|-\(\frac{8}{9}\)| = \(\frac{8}{9}\)
|\(\frac{8}{9}\)| = \(\frac{8}{9}\)
Question 5.
Morgan plots the point (4, –7) on a coordinate plane. If she reflects the point across the y-axis, what are the coordinates of the reflected point?
Type below:
___________
Answer:
(-4, -7)
Explanation:
Morgan plots the point (4, –7) on a coordinate plane. If she reflects the point across the y-axis, it will be (-4, -7)

Chapter 4 Review/Test – Page No. 261
Question 1.
Kendra has 4 necklaces, 7 bracelets, and 5 rings. Draw a model to show the ratio that compares rings to bracelets
Type below:___________
Answer:
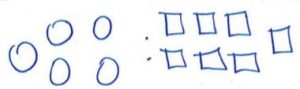
Question 2.
There are 3 girls and 2 boys taking swimming lessons. Write the ratio that compares the girls taking swimming lessons to the total number of students taking swimming lessons.
Type below:
___________
Answer:
3 : 5
Explanation:
There are 3 girls and 2 boys taking swimming lessons.
the total number of students taking swimming lessons = 5
3 : 5
Question 3.
Luis adds 3 strawberries for every 2 blueberries in his fruit smoothie. Draw a model to show the ratio that compares strawberries to blueberries.
Type below:
___________
Answer:

Question 4.
Write the ratio 3 to 10 in two different ways.
Type below:
___________
Answer:
3/10, 3 : 10
Question 5.
Alex takes 3 steps every 5 feet he walks. As Alex continues walking, he takes more steps and walks a longer distance. Complete the table by writing two equivalent ratios.
Type below:
___________
Answer:
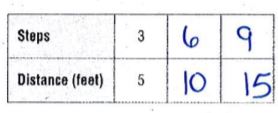
Explanation:
Alex takes 3 steps every 5 feet he walks. As Alex continues walking, he takes more steps and walks a longer distance.
3/5 × 2/2 = 6/10
3/5 × 3/3 = 9/15
Page No. 262
Question 6.
Sam has 3 green apples and 4 red apples. Select the ratios that compare the number of red apples to the total number of apples. Mark all that apply.
Options:
a. 4 to 7
b. 3 to 7
c. 4 : 7
d. 4 : 3
e. \(\frac{3}{7}\)
f. \(\frac{4}{7}\)
Answer:
a. 4 to 7
c. 4 : 7
f. \(\frac{4}{7}\)
Explanation:
Sam has 3 green apples and 4 red apples.
the total number of apples = 3 + 4 = 7
4 : 7
Question 7.
Jeff ran 2 miles in 12 minutes. Ju Chan ran 3 miles in 18 minutes. Did Jeff and Ju Chan run the same number of miles per minute? Complete the tables of equivalent ratios to support your answer.
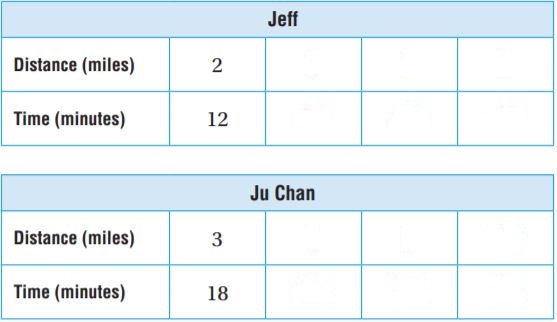
Type below:
___________
Answer:
Explanation:
2/12 × 2/2 = 4/24
2/12 × 3/3 = 6/39
2/12 × 4/4 = 8/48
3/18 × 2/2 = 6/36
3/18 × 3/3 = 9/24
3/18 × 4/4 = 12/72
Page No. 263
Question 9.
Determine whether each ratio is equivalent to \(\frac{1}{2}, \frac{2}{3}, \text { or } \frac{4}{7}\). Write the ratio in the correct box.

Type below:
___________
Answer:
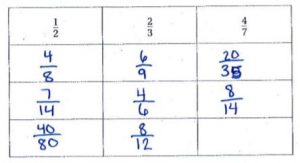
Explanation:
1/2 × 2/2 = 4/8
7/14 ÷ 2/2 = 1/2
20/35 ÷ 5/5 = 4/7
40/80 ÷ 40/40 = 1/2
8/14 ÷ 2/2 = 4/7
4/6 ÷ 2/2 = 2/3
8/12 ÷ 4/4 = 2/3
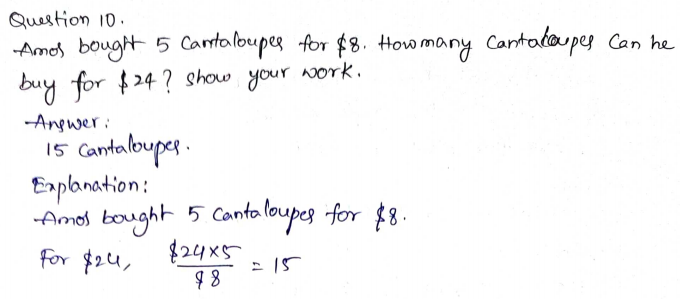
Question 11.
Camille said \(\frac{4}{5}\) is equivalent to \(\frac{24}{30}\). Check her work by making a table of equivalent ratios.
Type below:
___________
Answer:

Question 12.
A box of oat cereal costs $3.90 for 15 ounces. A box of rice cereal costs $3.30 for 11 ounces. Which box of cereal costs less per ounce? Use numbers and words to explain your answer.
Type below:
___________
Answer:
A box of oat cereal costs $3.90 for 15 ounces.
$3.90/15 = $0.26
A box of rice cereal costs $3.30 for 11 ounces.
$3.30/11 = $0.3
$0.26 < $0.3
Page No. 264
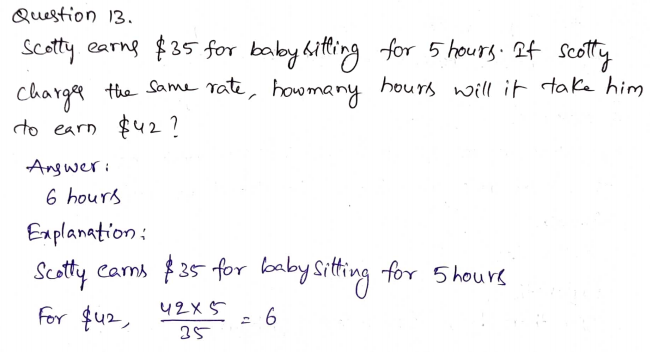
Question 14.
Use a unit rate to find the unknown value.
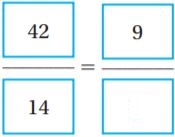
Type below:
___________
Answer:
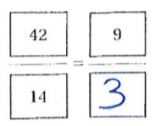
Explanation:
(9 × 42)/14 = 3
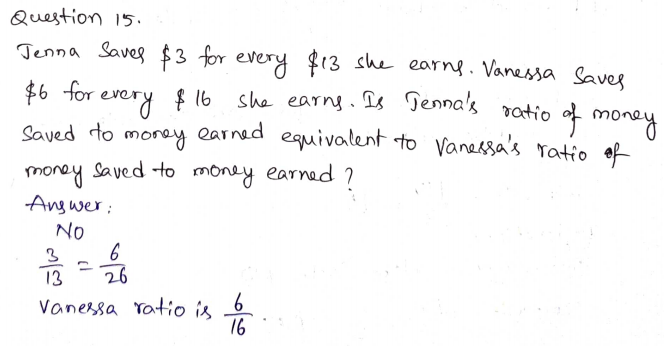
Question 16.
The Hendersons are on their way to a national park. They are traveling at a rate of 40 miles per hour. Use the ordered pairs to graph the distance traveled over time

Type below:
___________
Answer:
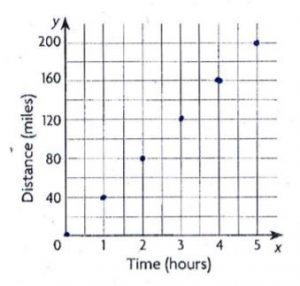
Page No. 265
Question 17.
Abby goes to the pool to swim laps. The graph shows how far Abby swam over time. Use equivalent ratios to find how far Abby swam in 7 minutes
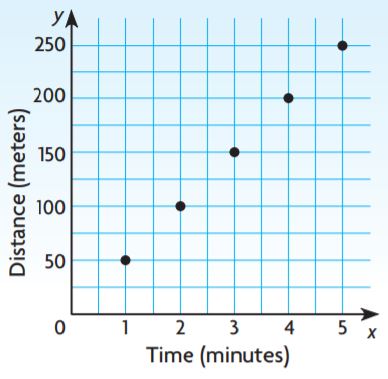
_____ meters
Answer:
350 meters
Explanation:
50/1 × 7/7 = 350/7
Question 18.
Caleb bought 6 packs of pencils for $12.
Part A
How much will he pay for 9 packs of pencils? Use numbers and words to explain your answer
$ _____
Answer:
$18
Explanation:
Caleb bought 6 packs of pencils for $12.
6/12 = 1/2 × 9/9 = 9/18
So, $18 is the answer
Question 18.
Part B
Describe how to use a bar model to solve the problem.
Type below:
___________
Answer:
Take the known ratio and identify the unknown value using known ratio.
Page No. 266
Question 19.
A rabbit runs 35 miles per hour. Select the animals who run at a faster unit rate per hour than the rabbit. Mark all that apply.
Options:
a. Reindeer: 100 miles in 2 hours
b. Ostrich: 80 miles in 2 hours
c. Zebra: 90 miles in 3 hours
d. Squirrel: 36 miles in 3 hours
Answer:
a. Reindeer: 100 miles in 2 hours
b. Ostrich: 80 miles in 2 hours
Explanation:
A rabbit runs 35 miles per hour.
35/1
100/2 = 50/1
80/2 = 40/1
90/3 = 30/1
36/3 = 12/1
Question 20.
Water is filling a bathtub at a rate of 3 gallons per minute.
Part A
Complete the table of equivalent ratios for the first five minutes of the bathtub filling up.

Type below:
___________
Answer:

Question 20.
Part B
Emily said there will be 36 gallons of water in the bathtub after 12 minutes. Explain how Emily could have found her answer
Type below:
___________
Answer:
Emily said there will be 36 gallons of water in the bathtub after 12 minutes.
36/12 ÷ 12/12 = 3/1
She can find the answer using the unit rate.
Conclusion:
Hope the solutions provided in Go Math Grade 6 Answer Key Chapter 4 Model Ratios helped you to enhance your math skills. Also, this Go Math Answer Key helps you to score the highest marks in the exam. Share this pdf link with your friends so that they can overcome the difficulties in maths. All the Best!!!
