Go Math Grade 7 Answer Key Chapter 1 Adding and Subtracting Integers

Are you searching for Go Math Grade 7 Solutions? then what are you waiting for Download Go Math Grade 7 Answer Key Chapter 1 Adding and Subtracting Integers pdf for free of cost. Here we are providing the step by step explanation for all the questions in Go Math Grade 7 Answer Key for Chapter 1 Adding and Subtracting Integers.

Go Math Grade 7 Answer Key Chapter 1 Adding and Subtracting Integers

We suggest the students check out the topics of Grade 7 chapter 1 before you start your preparation for exams. The chapter Adding and Subtracting Integers contains topics such as Adding Integers with the Same Sign, Different sign, Subtracting Integers, Applying Addition and Subtraction of Integers, and so on. Tap the below links and try to solve the questions provided in the Go Math Grade 7 Solution Key Chapter 1 Adding and Subtracting Integers.

Chapter 1 – Adding Integers with the Same Sign

• Adding Integers with the Same Sign – Guided Practice – Page No. 10
• Adding Integers with the Same Sign – Independent Practice – Page No. 11
• Adding Integers with the Same Sign – Page No. 12

Chapter 1 – Adding Integers with Different Signs

• Adding Integers with Different Signs – Guided Practice – Page No. 16
• Adding Integers with Different Signs – Independent Practice – Page No. 17
• Adding Integers with Different Signs – Page No. 18

Chapter 1 – Subtracting Integers

• Subtracting Integers – Guided Practice – Page No. 22
• Subtracting Integers – Independent Practice – Page No. 23
• Subtracting Integers – Page No. 24

Chapter 1 – Applying Addition and Subtraction of Integers

• Applying Addition and Subtraction of Integers – Guided Practice – Page No. 28
• Applying Addition and Subtraction of Integers – Independent Practice – Page No. 29

Chapter 1 – MODULE 1

• Module Quiz – Ready to Go On – Page No. 31
• Module Quiz – MODULE 1 MIXED REVIEW – Page No. 32
• MODULE 1 MIXED REVIEW
• Module 1 Review – Adding and Subtracting Integers – Page No. 103

Adding Integers with the Same Sign – Guided Practice – Page No. 10

Find each sum.

Question 1.
-5 + (-1)

a. How many counters are there?
_______ counters

Answer: 6

Explanation:
By seeing the above pictures we can say that there are 6 counters.

Question 1.
b. Do the counters represent positive or negative numbers?
____________

Answer: negative numbers

Explanation:
The counters are red so they represent negative numbers.

Question 1.
c. -5 + (-1) =
_______

Answer: -6

Explanation:
There are 6 counters so -5 + (-1) = – 6

Question 2.
-2 + (-7)

a. How many counters are there?
_______ counters

Answer: 9

Explanation:
The above figure shows that there are 9 counters.

Question 2.
b. Do the counters represent positive or negative numbers?
____________

Answer: negative numbers

Explanation:
The counters are red so they represent the negative numbers.

Question 2.
c. -2 + (-7) =
_______

Answer: -9

Explanation:
There are 9 counters so -2 + (-7) = -9
The answer is -9.

Model each addition problem on the number line to find each sum.

Question 3.
-5 + (-2) =

_______

Answer: -7

Explanation:
Remember if the number being added is positive more units go to the right and if the number being added is negative more units to the left.
Since we are adding the negative number starting from -5, we move 2 units to the left. This results in -7.

Question 4.
-1 + (-3) =

_______

Answer: -4

Explanation:
Remember if the number being added is positive more units go to the right and if the number being added is negative more units to the left.
Since we are adding a negative number starting from -1, we move 3 units to left. This results in -4.

Question 5.
-3 + (-7) =

_______

Answer: -10

Explanation:
Remember if the number being added is positive more units go to the right and if the number being added is negative more units to the left.
Since we are adding a negative number starting from -3, we move 7 units to left. This results in -10.

Question 6.
-4 + (-1) =

_______

Answer: -5

Explanation:
Remember if the number being added is positive more units go to the right and if the number being added is negative more units to the left.
Since we are adding a negative number starting from -4, we move 1 unit to left. This results in -5.

Question 7.
-2 + (-2) =

_______

Answer: -4

Explanation:
Remember if the number being added is positive more units go to the right and if the number being added is negative more units to the left.
Since we are adding the negative number starting at -2, we move 2 units to the left which gives the result -4.

Question 8.
-6 + (-8) =

_______

Answer: -14

Explanation:
Remember if the number being added is positive more units go to the right and if the number being added is negative more units to the left.
Since we are adding the negative number starting from -6 we have to move 8 units to the left which shows the result -14.

Find each sum.

Question 9.
-5 + (-4) =
_______

Answer: -9

Explanation:
In adding two integers with the same signs you add both integers and keep the common sign.
Since -5 + (-4) has the same sign we add their absolute value and keep the same sign.
-5 + (-4) = -(5 + 4) = -9

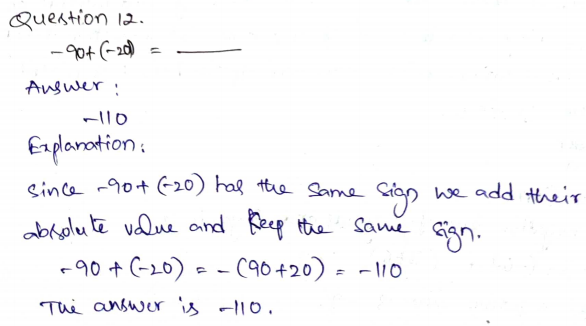
Question 13.
-52 + (-48) =
_______

Answer: -100

Explanation:
In adding two integers with the same signs you add both integers and keep the common sign.
Since -52 + (-48) has the same sign we add their absolute value and keep the same sign.
-52 + (-48) = -(52 + 48)
= -100
The answer is -100.

Question 14.
5 + 198 =
_______

Answer: 203

Explanation:
In adding two integers with the same signs you add both integers and keep the common sign.
Since 5 + 198 has the same sign we add their absolute value and keep the same sign.
5 + 198 = 203
The answer is 203.

Question 15.
-4 + (-5) + (-6) =
_______

Answer: -15

Explanation:
In adding two integers with the same signs you add both integers and keep the common sign.
Since -4 + (-5) + (-6) has the same sign we add their absolute value and keep the same sign.
-4 + (-5) + (-6) = -(4 + 5 + 6)
= -15
The answer is -15.

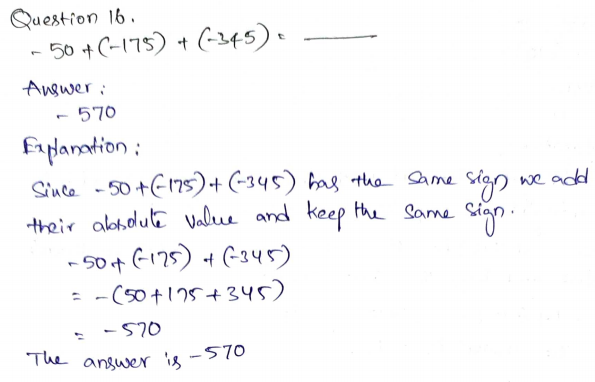
Adding Integers with the Same Sign – Independent Practice – Page No. 11

Question 18.
Represent Real-World Problems Jane and Sarah both dive down from the surface of a pool. Jane first dives down 5 feet and then dives down 3 more feet. Sarah first dives down 3 feet and then dives down 5 more feet.
a. Multiple Representations Use the number line to model the equation -5 + (-3) = -3 + (-5).

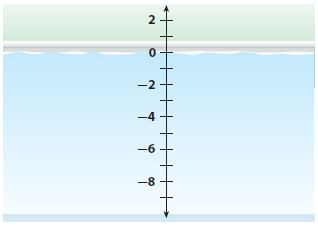
Type below:
______________

Answer: -8

Explanation:
Start at -3 and move 5 units down for one number line. Next, start at -5 and move down 3 units for another number line.
Both have a final answer of -8.
So, -5 + (-3) = -3 + (-5) = -8.

Question 18.
b. Does the order in which you add two integers with the same sign affect the sum? Explain.
_______

Answer: no

Explanation:

Based on the results of part a, the order doesn’t matter. Since the commutative properties of addition hold for the sum of two negative numbers.

Question 19.
A golfer has the following scores for a 4-day tournament.

What was the golfer’s total score for the tournament?
_______

Answer: -11

Explanation:
The total score is the sum of each day’s score
= -3 + (-1) + (-5) + (-2)
= -(3 + 1 + 5 + 2)
= -11
Thus the total score for 4 days tournament is -11.

Question 21.
When the quarterback is sacked, the team loses yards. In one game, the quarterback was sacked four times. What was the total sack yardage?

_______

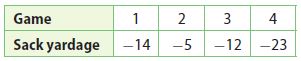
Answer: -54

Explanation:
The total sack yardage = -14 + (-5) + (-12) + (-23)
= -(14 + 5 + 12 + 23)
= -54
Therefore the total sack yardage is -54.

Question 22.
Multistep The temperature in Jonestown and Cooperville was the same at 1:00. By 2:00, the temperature in Jonestown dropped 10 degrees, and the temperature in Cooperville dropped 6 degrees. By 3:00, the temperature in Jonestown dropped 8 more degrees, and the temperature in Cooperville dropped 2 more degrees.
a. Write an equation that models the change to the temperature in Jonestown since 1:00.
Type below:
______________

Answer: J = T – 18

Explanation:
Let J be the final temperature and T be the initial temperature. Then the equation is J = T + (-10) + (-8)
J = T – 18

Question 22.
b. Write an equation that models the change to the temperature in Cooperville since 1:00.
Type below:
______________

Answer: C = T – 8

Explanation:
Let C be the final temperature and T be the initial temperature. Then the equation is C = T + (-6) + (-2)
C = T – 8

Question 22.
c. Where was it colder at 3:00, in Jonestown or Cooperville?
__________

Answer: Jonestown

Explanation:
Since they both started at the same temperature and Jonestown dropped a total of 18 degrees while Cooperville dropped a total of 8 degrees, Jonestown is colder.

Adding Integers with the Same Sign – Page No. 12

H.O.T. FOCUS ON HIGHER ORDER THINKING

Question 24.
Multistep On Monday, Jan made withdrawals of $25, $45, and $75 from her savings account. On the same day, her twin sister Julie made withdrawals of $35, $55, and $65 from her savings account.
a. Write a sum of negative integers to show Jan’s withdrawals on Monday. Find the total amount Jan withdrew.
Jan withdrew $ _______

Answer: 145

Explanation:
Each withdrawal is represented by a negative integer so find the sum of those negative integers = -25 + (-45) + (-75)
= -(25 + 45 + 75)
= -145
Thus Jan withdrew $145.

Question 24.
b. Write a sum of negative integers to show Julie’s withdrawals on Monday. Find the total amount Julie withdrew.
Julie withdrew $ _______

Answer: 155

Explanation:
Each withdrawal is represented by a negative integer so find the sum of those negative integers
= -35 + (-55) + (-65)
= – (35 + 55 + 65)
= -155
The total amount Julie withdrew is -$155.

Question 24.
c. Julie and Jan’s brother also withdrew money from his savings account on Monday. He made three withdrawals and withdrew $10 more than Julie did. What are three possible amounts he could have withdrawn?
Type below:
______________

Answer:

If he withdrew $10 more than Julie then he withdrew $165 in total. The possible amounts could then be $35, $55, $75.

Question 26.
Critique Reasoning The absolute value of the sum of two different integers with the same sign is 8. Pat says there are three pairs of integers that match this description. Do you agree? Explain.
__________

Answer: Disagree

Explanation:
Pat is saying that x + y = 8 is true for only three pairs of numbers with the same sign.
This is not true though. The pairs could be 1, 7, 2 and 6, 3, 5, 4 and -4, -1 and -7, -2 and -6, -3 and -5 and -4, -4.

Adding Integers with Different Signs – Guided Practice – Page No. 16

Use a number line to find each sum.

Question 1.
9 + (-3) =

_______

Answer: 6

Explanation:
Remember if the number being added is positive more units go to the right and if the number being added is negative more units to the left.
Since we are adding a negative number starting from 9, move 3 units to the left. This results in 6.

Question 2.
-2 + 7 =

_______

Answer: 5

Explanation:
Remember if the number being added is positive more units go to the right and if the number being added is negative more units to the left.
Since we are adding a positive number starting from -2 we move 7 units to the right. This results in 5.

Question 3.
-15 + 4 =

_______

Answer: -11

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding a positive number starting from -15, we move 4 units to the right. This results in -11

Question 4.
1 + (-4) =

_______

Answer: -3

Explanation:
Remember if the number being added is positive more number of units going to the right and if the number being added is negative more number of units to the left.
Since we are adding the negative number starting from 1, we move 4 units to the left. This results in -3.

Circle the zero pairs in each model. Find the sum.

Question 5.
-4 + 5 =

_______

Answer: 1

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
Above is an illustration of which are the zero pairs and what remains. In this item 1 yellow counter remains which means the sum is 1.

Question 6.
-6 + 6 =

_______

Answer: 0

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
Above is an illustration of which are the zero pairs and what remains. In this item, there are no counters so the sum is 0.

Question 7.
2 + (-5) =

_______

Answer: -3

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
Above is an illustration of which are the zero pairs and what remains. In this item, 3 red counters are remaining so the sum is -3.

Question 8.
-3 + 7 =

_______

Answer: 4

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
Above is an illustration of which are the zero pairs and what remains. In this item, 4 yellow counters remain so the sum is 4.

Find each sum.

Question 9.
-8 + 14 =
_______

Answer: 6

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
Here we are the opposite number with the negative number.
-8 + 14 = 6
The more significant number is having a positive sign so the sum is 6.

Question 12.
14 + (-14) =
_______

Answer: 0

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
14 + (-14) =14 – 14 = 0

Question 13.
0 + (-5) =

Answer: -5

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
0 + (-5) = 0 – 5 = -5
The larger is having a negative sign so the sum is -5.

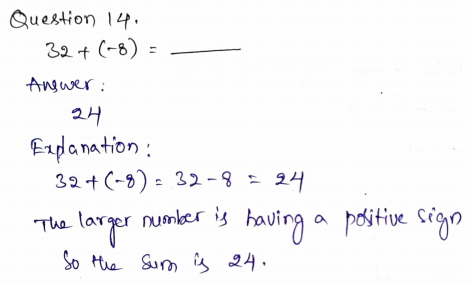
Adding Integers with Different Signs – Independent Practice – Page No. 17

Find each sum.

Question 16.
-15 + 71 =
_______

Answer: 56

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
-15 + 71 = |71| – |-15|
= 71 – 15
= 56

Question 17.
-53 + 45 =
_______

Answer: -8

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
-53 + 45 = |-53| – |45|
53 – 45 = 8
The larger number is having the negative symbol so the answer is -8.

Question 18.
-79 + 79 =
_______

Answer: 0

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
79 + (-79) = |79| – |-79|
79 – 79 = 0

Question 19.
-25 + 50 =
_______

Answer: 25

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
-25 + 50 = |50| – |-25|
50 – 25 = 25

Question 20.
18 + (-32) =
_______

Answer: -14

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
18 + (-32) = |-32| – |18|
32 – 18 = 14
The larger number is having a negative sign so the answer is -14.

Question 21.
5 + (-100) =
_______

Answer: -95

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
5 + (-100) = |-100| – |5|
100 – 5 = 95
The larger number is having a negative sign so the answer is -95.

Question 22.
-12 + 8 + 7 =
_______

Answer: 3

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
-12 + 8 + 7 = -12 + (8 + 7)
For the terms have different signs, we subtract the lesser absolute value from the greater absolute value and use the sign of the integer with the greater absolute value for the sum: 3
-12 + 15 = 3

Question 23.
-8 + (-2) + 3 =
_______

Answer: -7

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger and keep the sign of the number with the larger absolute value.
-(8 + 2) + 3
For the terms have different signs, we subtract the lesser absolute value from the greater absolute value and use the sign of the integer with the greater absolute value for the sum: -7
-10 + 3 = -7

Question 24.
15 + (-15) + 200 =
_______

Answer: 200

Explanation:
We are given the expression:
15 + (-15) + 200 = 0 + 200
The sum of the opposite number is 0.
0 + 200 = 200

Question 27.
A soccer team is having a car wash. The team spent $55 on supplies. They earned $275, including tips. The team’s profit is the amount the team made after paying for supplies. Write a sum of integers that represents the team’s profit.
Type below:
____________

Answer: 220

Explanation:
(-55) + (+275)
The money spent on supplies diminishes the profit, so they contribute to the profit with -55, while the earned money increases the profit, so they contribute to the profit with +275.
The sum of integers that represents the team’s profit is:
(-55) + (+275) = (275 -55) = 220

Question 28.
As shown in the illustration, Alexa had a negative balance in her checking account before depositing a $47.00 check. What is the new balance of Alexa’s checking account?

$ _______

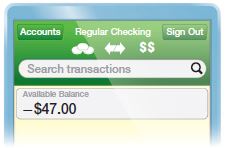
Answer: 0

Explanation:
(-47) + 47 = 0
The new balance consists of the sum between the old balance and the amount she deposits: 0

Question 29.
The sum of two integers with different signs is 8. Give two possible integers that fit this description.
Type below:
____________

Answer: 10 and -2

Explanation:
10 and 2
10 – 2 = 8
Because the sum of the two numbers is positive and the two numbers have different signs, it means the absolute value of the positive number is 8 units greater than the absolute value of the negative number. First, we find two positive numbers which are different by 8, which will be the positive values of our numbers.
10 and -2
Our positive number will be a greater one while our negative number will be the smaller one (-2). So the desired numbers are:
10 + (-2) = 8
12 + (-4) = 8
15 + (-7) = 8

Question 30.
Multistep Bart and Sam played a game in which each player earns or loses points in each turn. A player’s total score after two turns is the sum of his points earned or lost. The player with the greater score after two turns wins. Bart earned 123 points and lost 180 points. Sam earned 185 points and lost 255 points. Which person won the game? Explain.
____________

Answer: Bart

Explanation:
123 + (-180) = -(180 – 123) = -57
The person who has the greatest number of points after 2 turns wins.
We find the number of points Bart has, by adding the number of points from the two turns:
185 + (-255) = -(255 – 185) – 70
We find the number of points Sam has, by adding the number of points from the two turns:
The winner is Bart because -57 is greater than -70.

Adding Integers with Different Signs – Page No. 18

H.O.T. FOCUS ON HIGHER ORDER THINKING

Question 31.
Critical Thinking Explain how you could use a number line to show that -4 + 3 and 3 + (-4) have the same value. Which property of addition states that these sums are equivalent?
____________ Property of Addition

Answer: Commutative property of addition

Explanation:
In order to prove that -4 + 3 and 3 + (-4) have the same value we use the number line twice: -1 we start from -4 and we move 3 units in the positive direction to the right we get the sum -1.
We start from 3 and we move 4 units in the negative direction to the left where we find again -1.
The property of addition which states that the sum is the same no matter the order in which we add the terms is called commutative property.

Question 32.
Represent Real-World Problems Jim is standing beside a pool. He drops weight from 4 feet above the surface of the water in the pool. The weight travels a total distance of 12 feet down before landing on the bottom of the pool. Explain how you can write a sum of integers to find the depth of the water.
Type below:
____________

Answer: 12 + (-4) = 8

Explanation:
Given that,
Jim is standing beside a pool.
He drops weight from 4 feet above the surface of the water in the pool.
The weight travels a total distance of 12 feet down before landing on the bottom of the pool.
12 + (-4) = 12 – 4 = 8
The depth of the water can be calculated by adding to the total distance of 12 feet the negative distance of -4 feet.

Question 33.
Communicate Mathematical Ideas Use counters to model two integers with different signs whose sum is positive. Explain how you know the sum is positive.
Type below:
____________

Answer: The result is positive because there are more positive counters than negative counters.

Explanation:
○○○○○○○
●●●
Let’s model the sum 7 + (-3) using counters we use 7 white counters for the positive numbers and 3 black counters for the negative numbers.
We pair each white counter with a black counter their sum is being 0.
The result is +4 as we are left with 4 white counters.
The result is positive because there are more positive counters than negative counters.

Question 34.
Analyze Relationships You know that the sum of -5 and another integer is a positive integer. What can you conclude about the sign of the other integer? What can you conclude about the value of the other integer? Explain.
Type below:
____________

Answer:
We know that the sum is -5 and another integer is a positive integer. This means that the absolute value of the positive number is greater than the absolute value of -5.
The absolute value of -5 is 5, so the absolute value of the positive integer must be greater than 5. But because the number is positive, its absolute value is the number itself, so the positive number must be greater than 5.
-5 + 7 = 7 – 5 = 2

Subtracting Integers – Guided Practice – Page No. 22

Explain how to find each difference using counters.

Question 1.
5 – 8 =
_______

Answer: -3

Explanation:
5 – 8
We start with 5 black counters.
Since we have to subtract more black counters than we have (5 instead of 8), we add 3 zero pairs:
We subtract the 8 black counters: -3
We are left with 3 white counters, which means the result is -3.

Use a number line to find each difference.

Question 3.
− 4 − 5 = − 4 + ( _______ ) = _______

Answer: -9

Explanation:
-4 – 5
We have to compute the difference:
-4 – 5 = -(4 + 5)
On a number line, we start from -4 and we go to the left by 5 units:
-4 -5 = -9

Question 4.
1 − 4 = 1 + ( _______ ) = _______

Answer: -3

Explanation:
1 – 4
We have to compute the difference:
1 – 4 = 1 + (-4)
We replace the subtraction by addition with the opposite:
On a number line, we start from 1 and we go to the left by 4 units:
1 – 4 = – 3
The result is -3.

Solve.

Question 8.
-17 – 1 =
_______

Answer: -18

Explanation:
We have to perform the subtraction:
-17 – 1 = -17 + (-1)
We replace subtraction by addition with the opposite number:
-17 + (-1) = -18
We use the rule for adding integers: -18

Question 9.
0 – (-5) =
_______

Answer: 5

Explanation:
We have to perform the subtraction:
0 – (-5) = 0 + 5
We replace subtraction b addition with the opposite number:
0 + 5 = 5
We use the rule for adding integers: 5

Question 10.
1 – (-18) =
_______

Answer: 19

Explanation:
We have to perform the subtraction:
1 – (-18) = 1 + 18
We replace subtraction by addition with the opposite number:
1 + 18 = 19
We use the rule for adding integers: 19

Question 11.
15 – 1 =
_______

Answer: 14

Explanation:
We have to perform the subtraction:
15 – 1 = 14
We subtract the numbers directly as in this case it is simpler than to replace subtraction by addition with the opposite: 14

Question 12.
-3 – (-45) =
_______

Answer: 42

Explanation:
We have to perform the subtraction:
-3 – (-45) = -3 + 45
We replace subtraction by addition with the opposite number:
-3 + 45 = 42
We use the rule for adding integers: 42

Subtracting Integers – Independent Practice – Page No. 23

Question 16.
Theo had a balance of -$4 in his savings account. After making a deposit, he has $25 in his account. What is the overall change to his account?
$ _______

Answer: $29

Explanation:
Theo had a balance of -$4 in his savings account.
After making a deposit, he has $25 in his account.
25 – (-4)
The overall change to the account is the difference between the amount in the account after making the deposit and the amount before it, so we have to perform the subtraction.
25 – (-4) = 25 + 4
We change subtraction to addition with the opposite number:
25 + 4 = 29
We apply the rules for adding integers: $29

Question 17.
As shown, Suzi starts her hike at an elevation below sea level. When she reaches the end of the hike, she is still below sea level at -127 feet. What was the change in elevation from the beginning of Suzi’s hike to the end of the hike?

_______ feet

Answer: 98 feet

Explanation:
127 – (-225)
The change in the elevation from the beginning of Suzi’s hike to the end of the hike is the difference between the elevation at the end of the hike and the elevation at the beginning of it, so we have to perform the subtraction:
-127 – (-225) = -127 + 225
We change subtraction to addition with the opposite number:
-127 + 225 = 98
We apply the rules for adding integers: 98 feet

Question 20.
A scientist conducts three experiments in which she records the temperature of some gases that are being heated. The table shows the initial temperature and the
final temperature for each gas.

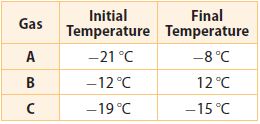
a. Write a difference of integers to find the overall temperature change for each gas.
Gas A: __________ °C increase
Gas B: __________ °C increase
Gas C: __________ °C increase

Answer:
We determine the overall change of temperature for each gas by subtracting the initial temperature from the final temperature.
Gas A:
-8 – (-21) = -8 + 21 = 13
Gas B:
12 – (-12) = 12 + 12 = 24
Gas C:
-15 – (-19) = -15 + 19 = 4

Question 20.
What If? Suppose the scientist performs an experiment in which she cools the three gases. Will the changes in temperature be positive or negative for this experiment? Why?
__________

Answer: Negative

Explanation:
Cooling the gases means diminishing their temperature, thus their final temperature will be lower than the initial temperature, so the change in temperature will be negative.

Subtracting Integers – Page No. 24

Question 21.
Analyze Relationships For two months, Nell feeds her cat Diet Chow brand cat food. Then for the next two months, she feeds her cat Kitty Diet brand cat food. The table shows the cat’s change in weight over 4 months.

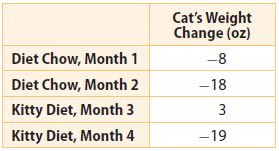
Which brand of cat food resulted in the greatest weight loss for Nell’s cat? Explain.
__________

Answer: Diet Chow

Explanation:
(-8) + (-18) = -26
We count the total change of weight resulted after using the diet chow for two months.
We count the total change of weight resulted after using the Kitty Diet for two months:
3 + (-19) = -16
This means that by using the Diet Chow the cat lost 26 oz, while using the Kitty Diet she lost 16 oz, thus the greatest loss of weight resulted in using the Diet Chow food.

FOCUS ON HIGHER ORDER THINKING

Question 22.
Represent Real-World Problems Write and solve a word problem that can be modeled by the difference -4 – 10.
Type below:
____________

Answer:
We have to write and solve a problem using the difference:
-4 – 10
For example:
Yesterday the temperature was -4 degrees. Today the temperature decreased by 10 degrees. What is the temperature today?
– 4 – 10 =- + (-10) = -14

Question 23.
Explain the Error When Tom found the difference -11 – (-4), he got -15. What might Tom have done wrong?
Type below:
____________

Answer:
We have to find the error in computing the difference:
-11 – (-4) = -15
In order to perform subtraction, Tom replaced it with addition, but he was wrong in adding -4 instead of adding its opposite 4.
The correct form is -11 – (-4) = -11 + 4 = -7

Applying Addition and Subtraction of Integers – Guided Practice – Page No. 28

Write an expression. Then find the value of the expression.

Question 1.
Tomas works as an underwater photographer. He starts at a position that is 15 feet below sea level. He rises 9 feet, then descends 12 feet to take a photo of a coral reef. Write and evaluate an expression to find his position relative to sea level when he took the photo.
_______ feet below sea level

Answer: 18 feet

Explanation:
When he rises, we add the distance. When he descends, we subtract the distance.
The initial position is -15. We write an expression to find his position relative to sea level when he took the photo:
-15 + 9 – 12 = (-15) + 9 + (-12)
(-15) + (-12) + 9
-(15 + 12) + 9
-27 + 9 = -18
Thus he was 18 feet below sea level when he took the photo.

Question 2.
The temperature on a winter night was -23 °F. The temperature rose by 5 °F when the sun came up. When the sun set again, the temperature dropped by 7 °F. Write and evaluate an expression to find the temperature after the sun set.
_______ °F

Answer: -25

Explanation:
When the temperature rises, we add the temperature. When the temperature drops, we subtract the temperature. The initial temperature is -23.
We write an expression to find the temperature after sunset:
-23 + 5 – 7 = -(23 + 7) + 5
-30 + 5 = -25
Thus the temperature is -25°F after sunset.

Find the value of each expression.

Question 4.
-6 + 15 + 15 =
_______

Answer: 24

Explanation:
We have to find the value of the expression:
-6 + 15 + 15 = – 6 + 30 = 24
-6 + 15 + 15 = 24

Question 5.
9 – 4 – 17 =
_______

Answer: -12

Explanation:
We have to find the value of the expression:
9 – 4 – 17 = 9 – (4 + 17)
= 9 – 21 = -12

Question 6.
50 – 42 + 10 =
_______

Answer: 18

Explanation:
We have to find the value of the expression:
50 + (-42) + 10 = 60 – 42
We use the commutative property:
60 – 42 = 18

Determine which expression has a greater value.

Question 10.
-12 + 6 – 4 or -34 – 3 + 39
___________

Answer:
We have to compare the expressions:
-12 + 6 – 4 or -34 – 3 + 39
We compute the first expression:
-12 + 6 – 4
-(12 + 4) + 6
-16 + 6 = -10
We compute the second expression:
-34 – 3 + 39
-(34 + 3) + 39
-37 + 39 = 2
2 > -10
Since 2 is greater than -10, the second expression is greater than the first expression.

Question 11.
21 – 3 + 8 or -14 + 31 – 6
___________

Answer:
We have to compare the expressions:
21 – 3 + 8 or -14 + 31 – 6
We compute the first expression:
21 – 3 + 8
21 + 8 – 3
21 + 5 = 26
We compute the second expression:
-14 + 31 – 6
31 – (14 + 6)
31 – 20 = 11
26 > 11
Since 26 is greater than 11, the first expression is greater than the second.

Question 12.
Explain how you can find the value of the expression -5 + 12 + 10 – 7.
Type below:
___________

Answer: 10

Explanation:
We have to find the value of the expression:
-5 + 12 + 10 – 7 = 12 + 10 – (5 + 7)
22 – 12 = 10

Applying Addition and Subtraction of Integers – Independent Practice – Page No. 29

Question 13.
Sports Cameron is playing 9 holes of golf. He needs to score a total of at most 15 over par on the last four holes to beat his best golf score. On the last four holes, he scores 5 over par, 1 under par, 6 over par, and 1 under par.
a. Write and find the value of an expression that gives Cameron’s score for 4 holes of golf.
Type below:
___________

Answer:
We write the expression that gives Cameron’s score for 4 holes:
5 – 1 + 6 – 1
5 + 6 – (1 + 1)
11 – 2 = 9

Question 13.
b. Is Cameron’s score on the last four holes over or under par?
Type below:
___________

Answer: The result shows that Cameron’s score is over par.

Question 13.
c. Did Cameron beat his best golf score?
_______

Answer:
Since his score of 9 is beaten his best score of 9 > 15.

Question 16.
Lee and Barry play a trivia game in which questions are worth different numbers of points. If a question is answered correctly, a player earns points. If a question is answered incorrectly, the player loses points. Lee currently has -350 points.

a. Before the game ends, Lee answers a 275-point question correctly, a 70-point question correctly, and a 50-point question incorrectly. Write and find the value of an expression to find Lee’s final score.
_______ points

Answer: -55 points

Explanation:
The initial score is -350 points. We write and find the value of an expression to find Lee’s final score:
-350 + 275 + 70 – 50
-(350 + 50) + 275 + 70
-400 + 345 = -55

Question 17.
b. Barry’s final score is 45. Which player had the greater final score?
___________

Answer: Since -55 < 45, it means Barry has a greater final score.

Question 17.
Multistep Rob collects data about how many customers enter and leave a store every hour. He records a positive number for customers entering the store each hour and a negative number for customers leaving the store each hour.

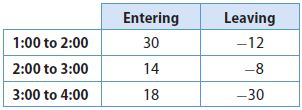
a. During which hour did more customers leave than arrive?
___________

Answer: 3:00 – 4:00

Explanation:
since in the last column, the only positive value is in the last position, the hour in which more customers leave than arrive is 3:00 – 4:00

Question 17.
b. There were 75 customers in the store at 1:00. The store must be emptied of customers when it closes at 5:00. How many customers must leave the store between 4:00 and 5:00?
_______ customers

Answer: 87

Explanation:
75 + 30 – 12 + 14 – 8 + 18 – 30
75 + 30 + 14 + 18 – (12 + 8 + 30)
137 – 50 = 87
Since there are 87 customers in the store at 4:00 and the store must be emptied at 5:00, the number of clients who must leave is 87.

Applying Addition and Subtraction of Integers – Page No. 30

The table shows the changes in the values of two friends’ savings accounts since the previous month.

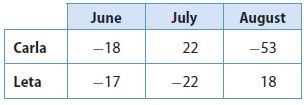
Question 18.
Carla had $100 in her account in May. How much money does she have in her account in August?
$ _______

Answer: $51

Explanation:
We are given the data:
100 – 18 + 22 – 53
100 + 22 -(18 + 53)
122 – 71 = 51
Thus Carla saved $51 in her account in August.

FOCUS ON HIGHER ORDER THINKING

Question 21.
Represent Real-World Problems Write and solve a word problem that matches the diagram shown.

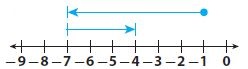
Type below:
___________

A diver leaves from a point situated 1 meter below the sea level. First, he dives 6 meters, then he rises 3 meters and stops. At which level under the sea level does he stop?
We start from the initial point -1, we add distance if he rises and we subtract distance when he dives. We determine the final level under the sea level where he stops:
-1 – 6 + 3
-(1 + 6) + 3
-7 + 3 = -4
-4 or 4 meters below sea level.

Question 23.
Draw Conclusions An expression involves subtracting two numbers from a positive number. Under what circumstances will the value of the expression be negative? Give an example.
Type below:
___________

Answer:
The sum of the two numbers to be subtracted from the positive number is a number, we will study this first. Since we subtract this number from the positive number and we get a negative number, it means that the number is greater than the positive number, therefore mandatory positive. This means the two numbers cannot be both negative.
Example:
10 – (7 + 5) = 10 – 12 = -2
-2 < 0

Module Quiz – Ready to Go On – Page No. 31

Adding Integers with the Same Sign

Add

Question 1.
−8 + (−6) = _______

Answer: -14

Explanation:
In adding two integers with the same signs you add both integers and keep the common sign.
−8 + (−6) = -(8 + 6) = -14

Question 2.
−4 + (−7) = _______

Answer: -11

Explanation:
In adding two integers with the same signs you add both integers and keep the common sign.
−4 + (−7) = – 4 – 7
-(4 + 7) = -11
−4 + (−7) = -11

Question 3.
−9 + (−12) = _______

Answer: -21

Explanation:
In adding two integers with the same signs you add both integers and keep the common sign.
−9 + (−12) = -9 – 12
-(9 + 12) = – 21
Thus −9 + (−12) = -21

Adding Integers with Different Signs

Add

Question 4.
5 + (−2) = _______

Answer: 3

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
5 + (−2) = 5 – 2 = 3
The larger number is having a positive sign thus the sum is 3

Question 5.
−8 + 4 = _______

Answer: -4

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
−8 + 4 = (-8) + 4 = -4
The larger number is having a negative sign thus the sum is -4.

Question 6.
15 + (−8) = _______

Answer: 7

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
15 + (−8) = 15 – 8 = 7
The larger number is having a positive sign thus the sum is 7.

Subtracting Integers

Subtract.

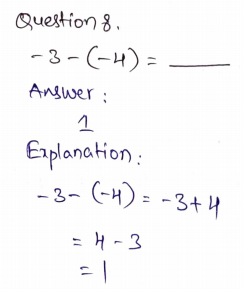
Applying Addition and Subtraction of Integers

Question 10.
A bus makes a stop at 2:30, letting off 15 people and letting on 9. The bus makes another stop ten minutes later to let off 4 more people. How many more or fewer people are on the bus after the second stop compared to the number of people on the bus before the 2:30 stop?
_______ people

Answer: 10

Explanation:
Assume that the total number of passengers on the bus before 2:30 was x
15 passengers got off and 9 got on.
number of passengers = x – 15 + 9
number of passengers = x -6
4 passengers got off the bus
number of passengers = (x-6) – 4
number of passengers = x – 10
The original number of passengers on the bus decreased by 10 after the second stop.

Question 11.
Cate and Elena were playing a card game. The stack of cards in the middle had 24 cards in it to begin with. Cate added 8 cards to the stack. Elena then took 12 cards from the stack. Finally, Cate took 9 cards from the stack. How many cards were left in the stack?
_______ cards

Answer: 11 cards

Explanation:
When cards are put to the stack, we perform addition.
When cards are taken from the stack we perform subtraction.
24 + 8 – 12 – 9
32 – (12 + 9)
32 – 21 = 11
Thus in the end the stack has 11 cards.

ESSENTIAL QUESTION

Question 12.
Write and solve a word problem that can be modeled by the addition of two negative integers.
Type below:
_____________

Answer: -25

Explanation:
A football team played two games. During the first game, the team lost 15 points and during the second game, it lost another 10 points. What is the change in the team’s score after these two games?
(-15) + (-10) = -25

Module Quiz – MODULE 1 MIXED REVIEW – Page No. 32

Assessment Readiness

Selected Response

Question 1.
Which expression has the same value as -3 + (-5):
Options:
a. -3 – (-5)
b. -3 + 5
c. -5 + (-3)
d. -5 – (-3)

Answer: -5 + (-3)

Explanation:
a. -3 – (-5)
-3 + 5 = 2
b. -3 + 5
5 – 3 = 2
c. -5 + (-3)
– 5 – 3 = -8
d. -5 – (-3)
-5 + 3 = -2
Thus the correct answer is option C.

Question 2.
A diver’s elevation is -30 feet relative to sea level. She dives down 12 feet. What is her elevation after the dive?
Options:
a. 12 feet
b. 18 feet
c. -30 feet
d. -42 feet

Answer: -42 feet

Explanation:
A diver’s elevation is -30 feet relative to sea level. She dives down 12 feet.
-30 -12 = (-30) + (-12) = -42 feet
Thus the correct answer is option D.

Question 3.
Which number line models the expression -3 + 5?
Options:
a.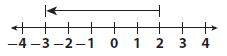
b.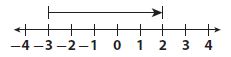
c.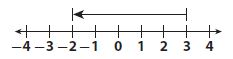
d.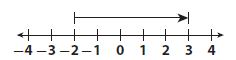

Answer:

Explanation:
-3 + 5
On the numeric line, his is modeled by starting at -3 and going right by 5 units. The number which models this is is:

Thus the correct answer is option B.

Question 4.
Which number can you add to 5 to get a sum of 0?
Options:
a. -10
b. -5
c. 0
d. 5

Answer: -5

Explanation:
The number we can add to 5 to get a sum of 0 is its opposite:
5 + (-5) = 0
The correct answer is option B.

Question 5.
The temperature in the morning was -3 °F. The temperature dropped 11 degrees by night. What was the temperature at night?
Options:
a. -14 °F
b. -8 °F
c. 8 °F
d. 14 °F

Answer: -14 °F

Explanation:
The temperature in the morning was -3 °F. The temperature dropped 11 degrees by night.
-3 + (-11) = -3 – 11 = -14°F
Therefore the correct answer is option A.

Question 6.
Which of the following expressions has the greatest value?
Options:
a. 3 – 7 + (-10)
b. 3 + 7 – (-10)
c. 3 – 7 – (-10)
d. 3 + 7 + (-10)

Answer: 3 + 7 – (-10)

Explanation:
a. 3 – 7 + (-10)
3 – 7 – 10 = 3 -(7 + 10) = 3 – 17 = -14
b. 3 + 7 – (-10)
3 + 7 + 10 = 20
c. 3 – 7 – (-10)
3 – 7 + 10 = 13 – 7 = 6
d. 3 + 7 + (-10)
10 – 10 = 0
Thus the correct answer is option B.

Mini-Task

Question 7.
At the end of one day, the value of a share of a certain stock was $12. Over the next three days, the change in the value of the share was -$1, then, -$1, and then $3.
a. Write an expression that describes the situation.
Type below:
____________

Answer:
We write an expression that describes the changes in the value of the share:
12 – 1 – 1 + 3

Question 7.
b. Evaluate the expression.
______

Answer: 13

Explanation:
12 – 1 – 1 + 3
12 + 3 – (1 + 1)
15 – 2 = 13

Question 7.
c. What does your answer to part b mean in the context of the problem?
Type below:
____________

Answer: After 3 days, the value of the share changed from $12 to $13.

MODULE 1

MIXED REVIEW

Assessment Readiness

Look at each expression. Does it have the same value as -6 – 4?

Select Yes or No for expressions A–C.

Question 8.
A. -6 + (-4)
______

Answer: Yes

Explanation:
-6 + (-4) = – 6 – 4
-6 + (-4) has the same value as – 6 – 4

Question 8.
B. -4 + (-6)
______

Answer: Yes

Explanation:
-4 + (-6) = -4 – 6
-4 + (-6) has the same value as – 6 – 4

Question 8.
C. 6 + (-4)
______

Answer: No

Explanation:
6 + (-4) = 6 – 4
6 – 4 ≠ – 6 – 4
So, 6 – 4 does not have the same value as – 6 – 4

Choose True or False for A–C.

Question 9.
A. x = 4 is the solution for x + 4 = 0.
i. True
ii. False

Answer: False

Explanation:
x + 4 = 0
x = 4
4 + 4 = 0
8 ≠ 0
So, the statement is false.

Question 9.
B. x = 24 is the solution for \(\frac{x}{3}\) = 8.
i. True
ii. False

Answer: True

Explanation:
\(\frac{x}{3}\) = 8
x = 24
24/3 = 8
8 = 8
Thus the statement is true.

Question 9.
C. x = 6 is the solution for 6x = 1
i. True
ii. False

Answer: False

Explanation:
6x = 1
x = 6
6(6) = 1
36 ≠ 1
Thus the statement is false.

Module 1 Review – Adding and Subtracting Integers – Page No. 103

EXERCISES

Question 1.
−10 + (−5) =
________

Answer: -15

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
-10 – 5 = -(10 + 5) = -15

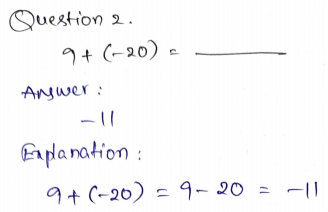
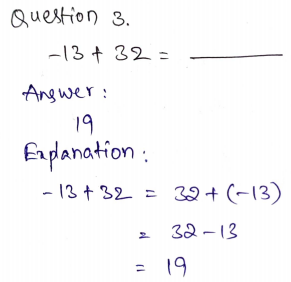
Question 5.
25 − (−4) =
________

Answer: 29

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
25 − (−4) = 25 + 4 = 29

Question 6.
−3 − (−40) =
________

Answer: 37

Explanation:
In adding two integers with the same sign, add their absolute value, and keep the common sign.
When adding two integers with opposite signs, subtract the smaller absolute value from the larger one and keep the sign of the number with the larger absolute value.
-3 – (-40) = -3 + 40 = 37

Question 7.
Antoine has $13 in his checking account. He buys some school supplies and ends up with $5 in his account. What was the overall change in Antoine’s account?
$ ________

Answer: $8

Explanation:
The overall change in his account is given by the difference between the final amount of money and the initial amount of money
5 – 13 = 5 + (-13) = -8
The amount in his account is decreased by $8.

Conclusion:
We believe that the solutions provided in Go Math Answer Key Grade 7 Chapter 1 Adding and Subtracting Integers are helpful for you. Also, share the Go Math Grade 7 Key Chapter 1 Adding and Subtracting Integers with your dear ones to help to overcome the issues in solving the integer problems. It helps to learn simple techniques to solve adding and subtracting integer problems. If you have any doubts you can clarify them by posting the comments in the below section.