Get Free Access to Download Go Math Grade 8 Answer Key Chapter 2 Exponents and Scientific Notation PDF from here. Start your preparation with the help of Go Math Grade 8 Answer Key. It is essential for all the students to learn the concepts of this chapter in-depth. So, make use of the Go Math Grade 8 Chapter 2 Exponents and Scientific Notation Solution Key links and go through the solutions.
Go Math Grade 8 Chapter 2 Exponents and Scientific Notation Answer Key
Check out the list of the topics before you start your preparation. You can step by step explanation for all the questions in HMH Go Math Grade 8 Answer Key Chapter 2 Exponents and Scientific Notation for free of cost. Quickly download Go Math Grade 8 Chapter 2 Answer Key PDF and fix the timetable to prepare.
Lesson 1: Integer Exponents
- Integer Exponents – Page No. 36
- Integer Exponents – Page No. 37
- Integer Exponents Lesson Check – Page No. 38
Lesson 2: Scientific Notation with Positive Powers of 10
- Scientific Notation with Positive Powers of 10 – Page No. 42
- Scientific Notation with Positive Powers of 10 – Page No. 43
- Scientific Notation with Positive Powers of 10 Lesson Check – Page No. 44
Lesson 3: Scientific Notation with Negative Powers of 10
- Scientific Notation with Negative Powers of 10 – Page No. 48
- Scientific Notation with Negative Powers of 10 – Page No. 49
- Scientific Notation with Negative Powers of 10 Lesson Check – Page No. 50
Lesson 4: Operations with Scientific Notation
- Operations with Scientific Notation – Page No. 54
- Operations with Scientific Notation – Page No. 55
- Operations with Scientific Notation Lesson Check – Page No. 56
Model Quiz
Mixed Review
Guided Practice – Integer Exponents – Page No. 36
Find the value of each power.
Question 1.
8−1 =
\(\frac{□}{□}\)
Answer:
\(\frac{1}{8}\)
Explanation:
Base = 8
Exponent = 1
8−1 = (1/8)1 = 1/8
Question 2.
6−2 =
\(\frac{□}{□}\)
Answer:
\(\frac{1}{36}\)
Explanation:
Base = 6
Exponent = 2
6−2 = (1/6)2 = 1/36
Question 3.
2560 =
______
Answer:
1
Explanation:
2560
Base = 256
Exponent = 0
Anything raised to the zeroth power is 1.
2560 = 1
Question 4.
102 =
______
Answer:
100
Explanation:
Base = 10
Exponent = 2
102 = 10 × 10 = 100
Question 5.
54 =
______
Answer:
625
Explanation:
Base = 5
Exponent = 4
54 = 5 × 5 × 5 × 5 = 625

Question 9.
11−3 =
\(\frac{□}{□}\)
Answer:
\(\frac{1}{1,331}\)
Explanation:
Base = 11
Exponent = 3
11−3 = (1/11)3 = (1/11) × (1/11) × (1/11) = 1/1,331
Use properties of exponents to write an equivalent expression.
Question 10.
4 ⋅ 4 ⋅ 4 = 4?
Type below:
_____________
Answer:
43
Explanation:
The same number 4 is multiplying 3 times.
The number of times a term is multiplied called the exponent.
So the base is 4 and the exponent is 3
4 ⋅ 4 ⋅ 4 = 43
Question 11.
(2 ⋅ 2) ⋅ (2 ⋅ 2 ⋅ 2) = 2? ⋅ 2? = 2?
Type below:
_____________
Answer:
25
Explanation:
The same number 2 is multiplying 5 times.
The number of times a term is multiplied called the exponent.
So the base is 2 and the exponent is 5
(2 ⋅ 2) ⋅ (2 ⋅ 2 ⋅ 2) = 22 ⋅ 23 = 25
Question 12.
\(\frac { { 6 }^{ 7 } }{ { 6 }^{ 5 } } \) = \(\frac{6⋅6⋅6⋅6⋅6⋅6⋅6}{6⋅6⋅6⋅6⋅6}\) = 6?
Type below:
_____________
Answer:
62
Explanation:
\(\frac { { 6 }^{ 7 } }{ { 6 }^{ 5 } } \) = \(\frac{6⋅6⋅6⋅6⋅6⋅6⋅6}{6⋅6⋅6⋅6⋅6}\)
Cancel the common factors
6.6
Base = 6
Exponent = 2
62
Question 13.
\(\frac { { 8 }^{ 12 } }{ { 8 }^{ 9 } } \) = 8?-? = 8?
Type below:
_____________
Answer:
83
Explanation:
\(\frac { { 8 }^{ 12 } }{ { 8 }^{ 9 } } \)
Bases are common. So, the exponents are subtracted
812-9 = 83
Question 14.
510 ⋅ 5 ⋅ 5 = 5?
Type below:
_____________
Answer:
512
Explanation:
Bases are common and multiplied. So, the exponents are added
Base = 5
Exponents = 10 + 1 + 1 = 12
512
Question 15.
78 ⋅ 75 = 7?
Type below:
_____________
Answer:
713
Explanation:
Bases are common and multiplied. So, the exponents are added
Base = 7
Exponents = 8 + 5 = 13
713
Question 16.
(62)4 = (6 ⋅ 6)? = (6 ⋅ 6) ⋅ (6 ⋅ 6) ⋅ (? ⋅ ?) ⋅ ? = 6?
Type below:
_____________
Answer:
68
Explanation:
(62)4 = (6 ⋅ 6)4 = (6 ⋅ 6) ⋅ (6 ⋅ 6) ⋅ (6 ⋅ 6) ⋅ (6 ⋅ 6) = 62 ⋅ 62 . 62 ⋅ 62
Bases are common and multiplied. So, the exponents are added
= 62+2+2+2
68
Simplify each expression.
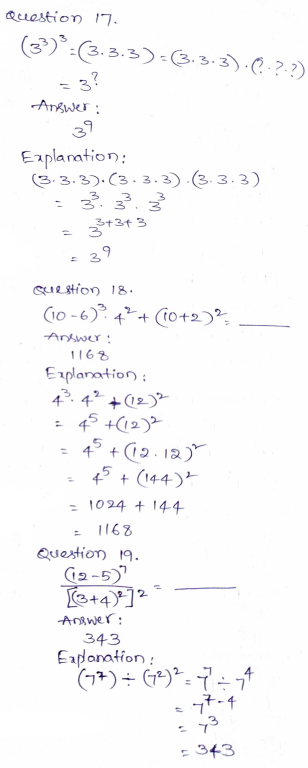
ESSENTIAL QUESTION CHECK-IN
Question 20.
Summarize the rules for multiplying powers with the same base, dividing powers with the same base, and raising a power to a power.
Type below:
______________
Answer:
The exponent “product rule” tells us that, when multiplying two powers that have the same base, you can add the exponents.
The quotient rule tells us that we can divide two powers with the same base by subtracting the exponents.
The “power rule” tells us that to raise a power to a power, just multiply the exponents.
Independent Practice – Integer Exponents – Page No. 37
Question 21.
Explain why the exponents cannot be added in the product 123 ⋅ 113.
Type below:
______________
Answer:
The exponent “product rule” tells us that, when multiplying two powers that have the same base, you can add the exponents.
The bases are not the same in the given problem.
=> (12)³ x (11)³
If we solve this equation following the rule of exponent will get the correct answer:
=> (12 x 12 x 12) x (11 x 11 x 11)
=> 1728 X 1331
=> the answer is 2 299 968
But if we add the exponent, the answer would be wrong
=> (12)³ x (11)³
=> 132^6
=> 5289852801024 which is wrong.
Question 22.
List three ways to express 35 as a product of powers.
Type below:
______________
Answer:
3¹ . 34
3² . 33
3³ . 32
Question 23.
Astronomy
The distance from Earth to the moon is about 224 miles. The distance from Earth to Neptune is about 227 miles. Which distance is the greater distance and about how many times greater is it?
_______ times
Answer:
(22)³ or 10,648 times
Explanation:
The distance from Earth to the moon is about 224 miles. The distance from Earth to Neptune is about 227 miles.
227 – 224 = (22)³
The greatest distance is from Earth to Neptune
The distance from Earth to Neptune is greater by (22)³ or 10,648 miles
Question 24.
Critique Reasoning
A student claims that 83 ⋅ 8-5 is greater than 1. Explain whether the student is correct or not.
______________
Answer:
83 ⋅ 8-5 is = 8-2
(1/8)²
(1/8) . (1/8) = 1/64 = 0.015
The student is not correct.
Find the missing exponent.
Question 28.
Communicate Mathematical Ideas
Why do you subtract exponents when dividing powers with the same base?
Type below:
______________
Answer:
To divide exponents (or powers) with the same base, subtract the exponents. The division is the opposite of multiplication, so it makes sense that because you add exponents when multiplying numbers with the same base, you subtract the exponents when dividing numbers with the same base.
Question 29.
Astronomy
The mass of the Sun is about 2 × 1027 metric tons, or 2 × 1030 kilograms. How many kilograms are in one metric ton?
________ kgs in one metric ton
Answer:
1,000 kgs in one metric ton
Explanation:
The mass of the Sun is about 2 × 1027 metric tons, or 2 × 1030 kilograms.
2 × 1027 metric tons = 2 × 1030 ki
1 metric ton = 2 × 1030 ki ÷ 2 × 1027 = (10)³ = 1,000 kgs in one metric ton
Question 30.
Represent Real-World Problems
In computer technology, a kilobyte is 210 bytes in size. A gigabyte is 230 bytes in size. The size of a terabyte is the product of the size of a kilobyte and the size of a gigabyte. What is the size of a terabyte?
Type below:
______________
Answer:
240 bytes
Explanation:
In computer technology, a kilobyte is 210 bytes in size. A gigabyte is 230 bytes in size. The size of a terabyte is the product of the size of a kilobyte and the size of a gigabyte.
terabyte = 210 bytes × 230 bytes = 210+30 bytes = 240 bytes
Integer Exponents – Page No. 38

A toy store is creating a large window display of different colored cubes stacked in a triangle shape. The table shows the number of cubes in each row of the triangle, starting with the top row.

Question 32.
Look for a Pattern
Describe any pattern you see in the table.
Type below:
______________
Answer:
As the number of rows increased, the number of cubes in each row by a multiple of 3.
Question 33.
Using exponents, how many cubes will be in Row 6? How many times as many cubes will be in Row 6 than in Row 3?
_______ times more cubes
Answer:
(33) times more cubes
Explanation:
For row 6, the number of cubes in each row = (36)
(36) ÷ (33) = (36-3) = (33)
(33) times more cubes
Question 34.
Justify Reasoning
If there are 6 rows in the triangle, what is the total number of cubes in the triangle? Explain how you found your answer.
______ cubes
Answer:
1,092 cubes
Explanation:
(31) + (32) + (33) + (34) + (35) + (36)
3 + 9 + 27 + 81 + 243 + 729 = 1,092
H.O.T.
Focus on Higher Order Thinking
Question 35.
Critique Reasoning
A student simplified the expression \(\frac { { 6 }^{ 2 } }{ { 36 }^{ 2 } } \) as \(\frac{1}{3}\). Do you agree with this student? Explain why or why not.
______________
Answer:
\(\frac { { 6 }^{ 2 } }{ { 36 }^{ 2 } } \)
(62) ÷ (62)²
(62) ÷ (64)
(62 – 4)
(6-2) = 1/36
I don’t agree with the student
Question 36.
Draw Conclusions
Evaluate –an when a = 3 and n = 2, 3, 4, and 5. Now evaluate (–a)n when a = 3 and n = 2, 3, 4, and 5. Based on this sample, does it appear that –an = (–a)n? If not, state the relationships, if any, between –an and (–a)n.
Type below:
______________
Answer:
–an when a = 3 and n = 2, 3, 4, and 5.
-3n
-(32 )= -9
(–a)n = -3 . -3 = 9
–an = (–a)n are not equal.
Persevere in Problem-Solving

Guided Practice – Scientific Notation with Positive Powers of 10 – Page No. 42
Write each number in scientific notation.
Question 1.
58,927
(Hint: Move the decimal left 4 places)
Type below:
______________
Answer:
5.8927 × (10)4
Explanation:
58,927
Move the decimal left 4 places
5.8927 × (10)4
Question 2.
1,304,000,000
(Hint: Move the decimal left 9 places.)
Type below:
______________
Answer:
1.304 × (10)9
Explanation:
1,304,000,000
Move the decimal left 9 places
1.304 × (10)9
Question 3.
6,730,000
Type below:
______________
Answer:
Explanation:
6,730,000
Move the decimal left 6 places
6.73 × (10)6
Question 4.
13,300
Type below:
______________
Answer:
Explanation:
13,300
Move the decimal left 4 places
1.33 × (10)4
Question 5.
An ordinary quarter contains about 97,700,000,000,000,000,000,000 atoms.
Type below:
______________
Answer:
Explanation:
97,700,000,000,000,000,000,000
Move the decimal left 22 places
9.77 × (10)22
Question 6.
The distance from Earth to the Moon is about 384,000 kilometers.
Type below:
______________
Answer:
3.84 × (10)6
Explanation:
384,000
Move the decimal left 6 places
3.84 × (10)6
Write each number in standard notation.
Question 7.
4 × 105
(Hint: Move the decimal right 5 places.)
Type below:
______________
Answer:
400,000
Explanation:
4 × 105
Move the decimal right 5 places
400,000
Question 8.
1.8499 × 109
(Hint: Move the decimal right 9 places.)
Type below:
______________
Answer:
1849900000
Explanation:
1.8499 × 109
Move the decimal right 9 places
1849900000
Question 9.
6.41 × 103
Type below:
______________
Answer:
6410
Explanation:
6.41 × 103
Move the decimal right 3 places
6410
Question 10.
8.456 × 107
Type below:
______________
Answer:
84560000
Explanation:
8.456 × 107
Move the decimal right 7 places
84560000
Question 11.
8 × 105
Type below:
______________
Answer:
800,000
Explanation:
8 × 105
Move the decimal right 5 places
800,000
Question 12.
9 × 1010
Type below:
______________
Answer:
90000000000
Explanation:
9 × 1010
Move the decimal right 10 places
90000000000
Question 13.
Diana calculated that she spent about 5.4 × 104 seconds doing her math homework during October. Write this time in standard notation.
Type below:
______________
Answer:
5400
Explanation:
Diana calculated that she spent about 5.4 × 104 seconds doing her math homework during October.
5.4 × 104
Move the decimal right 4 places
5400
Question 14.
The town recycled 7.6 × 106 cans this year. Write the number of cans in standard notation
Type below:
______________
Answer:
7600000
Explanation:
The town recycled 7.6 × 106 cans this year.
7.6 × 106
Move the decimal right 10 places
7600000
ESSENTIAL QUESTION CHECK-IN
Question 15.
Describe how to write 3,482,000,000 in scientific notation.
Type below:
______________
Answer:
3.482 × (10)9
Explanation:
3,482,000,000
Move the decimal left 9 places
3.482 × (10)9
Independent Practice – Scientific Notation with Positive Powers of 10 – Page No. 43
Paleontology
Use the table for problems 16–21. Write the estimated weight of each dinosaur in scientific notation.
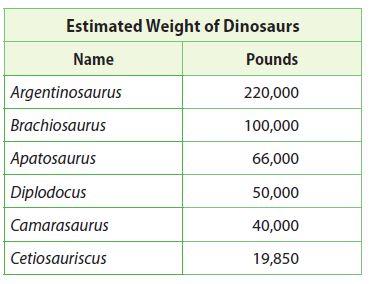
Question 16.
Apatosaurus ______________
Type below:
______________
Answer:
6.6 × (10)4
Explanation:
66,000
Move the decimal left 4 places
6.6 × (10)4
Question 17.
Argentinosaurus ___________
Type below:
______________
Answer:
2.2 × (10)5
Explanation:
220,000
Move the decimal left 5 places
2.2 × (10)5
Question 18.
Brachiosaurus ______________
Type below:
______________
Answer:
1 × (10)5
Explanation:
100,000
Move the decimal left 5 places
1 × (10)5
Question 19.
Camarasaurus ______________
Type below:
______________
Answer:
4 × (10)4
Explanation:
40,000
Move the decimal left 4 places
4 × (10)4
Question 20.
Cetiosauriscus ____________
Type below:
______________
Answer:
1.985 × (10)4
Explanation:
19,850
Move the decimal left 4 places
1.985 × (10)4
Question 21.
Diplodocus _____________
Type below:
______________
Answer:
5 × (10)4
Explanation:
50,000
Move the decimal left 4 places
5 × (10)4
Question 22.
A single little brown bat can eat up to 1,000 mosquitoes in a single hour. Express in scientific notation how many mosquitoes a little brown bat might eat in 10.5 hours.
Type below:
______________
Answer:
1.05 × (10)4
Explanation:
(1000 x 10.5) = 10500.
The little brown bat can eat 10500 mosquitoes in 10.5 hours.
1.05 × (10)4
Question 23.
Multistep
Samuel can type nearly 40 words per minute. Use this information to find the number of hours it would take him to type 2.6 × 105 words.
Type below:
______________
Answer:
Samuel can type 40 words per minute.
Then how many hours will it take for him to type 2.6 words times 10 to the power of five words
2.6 words time 10 to the power of 5
2.6 × (10)4
2.6 x 100 000 = 260 000 words in all.
Now, we need to find the number of words Samuel can type in an hour
40 words/minutes, in 1 hour there are 60 minutes
40 x 60
2,400 words /hour
Now, let’s divide the total of words he needs to type to the number of words he can type in an hour
260 000 / 2 400
108.33 hours.
Question 24.
Entomology
A tropical species of mite named Archegozetes longisetosus is the record holder for the strongest insect in the world. It can lift up to 1.182 × 103 times its own weight.
a. If you were as strong as this insect, explain how you could find how many pounds you could lift.
Type below:
______________
Answer:
Number of pounds you can lift by 1.182 × 103 by your weight
Question 24.
b. Complete the calculation to find how much you could lift, in pounds, if you were as strong as an Archegozetes longisetosus mite. Express your answer in both scientific notation and standard notation.
Type below:
______________
Answer:
scientific notation: 1.182 × 105
standard notation: 118200
Explanation:
1.182 × 103 × 102
1.182 × 105
118200
Question 25.
During a discussion in science class, Sharon learns that at birth an elephant weighs around 230 pounds. In four herds of elephants tracked by conservationists, about 20 calves were born during the summer. In scientific notation, express approximately how much the calves weighed all together.
Type below:
______________
Answer:
4.6 × 103
Explanation:
During a discussion in science class, Sharon learns that at birth an elephant weighs around 230 pounds. In four herds of elephants tracked by conservationists, about 20 calves were born during the summer.
Total weight of the claves = 230 × 20 = 4600
Move the decimal left 3 places
4.6 × 103
Question 26.
Classifying Numbers
Which of the following numbers are written in scientific notation?
0.641 × 103 9.999 × 104
2 × 101 4.38 × 510
Type below:
______________
Answer:
0.641 × 103
4.38 × 510
Scientific Notation with Positive Powers of 10 – Page No. 44
Question 27.
Explain the Error
Polly’s parents’ car weighs about 3500 pounds. Samantha, Esther, and Polly each wrote the weight of the car in scientific notation. Polly wrote 35.0 × 102, Samantha wrote 0.35 × 104, and Esther wrote 3.5 × 104.
a. Which of these girls, if any, is correct?
______________
Answer:
None of the girls is correct
Question 27.
b. Explain the mistakes of those who got the question wrong.
Type below:
______________
Answer:
Polly did not express the number such first part is greater than or equal to 1 and less than 10
Samantha did not express the number such first part is greater than or equal to 1 and less than 10
Esther did not express the exponent of 10 correctly
Question 28.
Justify Reasoning
If you were a biologist counting very large numbers of cells as part of your research, give several reasons why you might prefer to record your cell counts in scientific notation instead of standard notation.
Type below:
______________
Answer:
It is easier to comprehend the magnitude of large numbers when in scientific notation as multiple zeros in the number are removed and express as an exponent of 10.
It is easier to compare large numbers when in scientific notation as numbers are be expressed as a product of a number greater than or equal to 1 and less than 10
It is easier to multiply the numbers in scientific notation.
H.O.T.
Focus on Higher Order Thinking
Question 29.
Draw Conclusions
Which measurement would be least likely to be written in scientific notation: number of stars in a galaxy, number of grains of sand on a beach, speed of a car, or population of a country? Explain your reasoning.
Type below:
______________
Answer:
speed of a car
Explanation:
As we know scientific notation is used to express measurements that are extremely large or extremely small.
The first two are extremely large, then, they could be expressed in scientific notation.
If we compare the speed of a car and the population of a country, it is clear that the larger will be the population of a country.
Therefore, it is more likely to express that in scientific notation, so the answer is the speed of a car.
Question 30.
Analyze Relationships
Compare the two numbers to find which is greater. Explain how you can compare them without writing them in standard notation first.
4.5 × 106 2.1 × 108
Type below:
______________
Answer:
2.1 × 108
Explanation:
2.1 × 108 is greater because the power of 10 is greater in 2.1 × 108
Question 31.
Communicate Mathematical Ideas
To determine whether a number is written in scientific notation, what test can you apply to the first factor, and what test can you apply to the second factor?
Type below:
______________
Answer:
The first term must have one number before the decimal point
the second term (factor) must be 10 having some power.
Guided Practice – Scientific Notation with Negative Powers of 10 – Page No. 48
Write each number in scientific notation.
Question 1.
0.000487
Hint: Move the decimal right 4 places.
Type below:
______________
Answer:
4.87 × 10-4
Explanation:
0.000487
Move the decimal right 4 places
4.87 × 10-4
Question 2.
0.000028
Hint: Move the decimal right 5 places
Type below:
______________
Answer:
2.8 × 10-5
Explanation:
0.000028
Move the decimal right 5 places
2.8 × 10-5
Question 3.
0.000059
Type below:
______________
Answer:
5.9 × 10-5
Explanation:
0.000059
Move the decimal right 5 places
5.9 × 10-5
Question 4.
0.0417
Type below:
______________
Answer:
4.17 × 10-2
Explanation:
0.0417
Move the decimal right 2 places
4.17 × 10-2
Question 5.
Picoplankton can be as small as 0.00002 centimeters.
Type below:
______________
Answer:
2 × 10-5
Explanation:
0.00002
Move the decimal right 5 places
2 × 10-5
Question 6.
The average mass of a grain of sand on a beach is about 0.000015 gram.
Type below:
______________
Answer:
1.5 × 10-5
Explanation:
0.000015
Move the decimal right 5 places
1.5 × 10-5
Write each number in standard notation.
Question 7.
2 × 10-5
Hint: Move the decimal left 5 places.
Type below:
______________
Answer:
0.00002
Explanation:
2 × 10-5
Move the decimal left 5 places
0.00002
Question 8.
3.582 × 10-6
Hint: Move the decimal left 6 places.
Type below:
______________
Answer:
0.000003582
Explanation:
3.582 × 10-6
Move the decimal left 6 places
0.000003582
Question 9.
8.3 × 10-4
Type below:
______________
Answer:
0.00083
Explanation:
8.3 × 10-4
Move the decimal left 4 places
0.00083
Question 10.
2.97 × 10-2
Type below:
______________
Answer:
0.0297
Explanation:
2.97 × 10-2
Move the decimal left 2 places
0.0297
Question 11.
9.06 × 10-5
Type below:
______________
Answer:
0.0000906
Explanation:
9.06 × 10-5
Move the decimal left 5 places
0.0000906
Question 12.
4 × 10-5
Type below:
______________
Answer:
0.00004
Explanation:
4 × 10-5
Move the decimal left 5 places
0.00004
Question 13.
The average length of a dust mite is approximately 0.0001 meters. Write this number in scientific notation.
Type below:
______________
Answer:
1 × 10-4
Explanation:
The average length of a dust mite is approximately 0.0001 meters.
0.0001
Move the decimal right 4 places
1 × 10-4
Question 14.
The mass of a proton is about 1.7 × 10-24 grams. Write this number in standard notation.
Type below:
______________
Answer:
0.000000000000000000000017
Explanation:
The mass of a proton is about 1.7 × 10-24 grams.
1.7 × 10-24
Move the decimal left 24 places
0.000000000000000000000017
ESSENTIAL QUESTION CHECK-IN
Question 15.
Describe how to write 0.0000672 in scientific notation.
Type below:
______________
Answer:
6.72 × 10-5
Explanation:
0.0000672
Move the decimal right 5 places
6.72 × 10-5
Independent Practice – Scientific Notation with Negative Powers of 10 – Page No. 49
Use the table for problems 16–21. Write the diameter of the fibers in scientific notation.
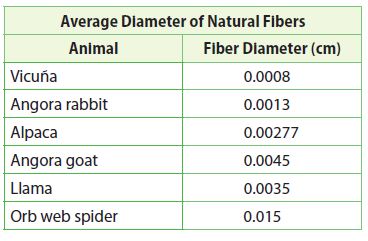
Question 16.
Alpaca _______
Type below:
______________
Answer:
2.77 × 10-3
Explanation:
0.00277
Move the decimal right 3 places
2.77 × 10-3
Question 17.
Angora rabbit _____________
Type below:
______________
Answer:
1.3 × 10-3
Explanation:
0.0013
Move the decimal right 3 places
1.3 × 10-3
Question 18.
Llama ____________
Type below:
______________
Answer:
3.5 × 10-3
Explanation:
0.0035
Move the decimal right 3 places
3.5 × 10-3
Question 19.
Angora goat ____________
Type below:
______________
Answer:
4.5 × 10-3
Explanation:
0.0045
Move the decimal right 3 places
4.5 × 10-3
Question 20.
Orb web spider ___________
Type below:
______________
Answer:
1.5 × 10-2
Explanation:
0.015
Move the decimal right 2 places
1.5 × 10-2
Question 21.
Vicuña __________
Type below:
______________
Answer:
8 × 10-4
Explanation:
0.0008
Move the decimal right 4 places
8 × 10-4
Question 22.
Make a Conjecture
Which measurement would be least likely to be written in scientific notation: the thickness of a dog hair, the radius of a period on this page, the ounces in a cup of milk? Explain your reasoning.
Type below:
______________
Answer:
The ounces in a cup of milk would be least likely to be written in scientific notation. The ounces in a cup of milk is correct.
Scientific notation is used for either very large or extremely small numbers.
The thickness of dog hair is very small as the hair is thin. Hence can be converted to scientific notation.
The radius of a period on this page is also pretty small. Hence can be converted to scientific notation.
The ounces in a cup of milk. There are 8 ounces in a cup, so this is least likely to be written in scientific notation.
Question 23.
Multiple Representations
Convert the length 7 centimeters to meters. Compare the numerical values when both numbers are written in scientific notation
Type below:
______________
Answer:
7 centimeters convert to meters
In every 1 meter, there are 100 centimeters = 7/100 = 0.07
Therefore, in 7 centimeters there are 0.07 meters.
7 cm is a whole number while 0.07 m is a decimal number
Scientific Notation of each number
7 cm = 7 x 10°
7 m = 1 x 10¯²
Scientific notation, by the way, is an expression used by the scientist to make a large number of very small number easy to handle.
Question 24.
Draw Conclusions
A graphing calculator displays 1.89 × 1012 as 1.89E12. How do you think it would display 1.89 × 10-12? What does the E stand for?
Type below:
______________
Answer:
1.89E-12. E= Exponent
Explanation:
Question 25.
Communicate Mathematical Ideas
When a number is written in scientific notation, how can you tell right away whether or not it is greater than or equal to 1?
Type below:
______________
Answer:
A number written in scientific notation is of the form
a × 10-n where 1 ≤ a < 10 and n is an integer
The number is greater than or equal to one if n ≥ 0.
Question 26.
The volume of a drop of a certain liquid is 0.000047 liter. Write the volume of the drop of liquid in scientific notation.
Type below:
______________
Answer:
4.7 × 10-5
Explanation:
The volume of a drop of a certain liquid is 0.000047 liter.
Move the decimal right 5 places
4.7 × 10-5
Question 27.
Justify Reasoning
If you were asked to express the weight in ounces of a ladybug in scientific notation, would the exponent of the 10 be positive or negative? Justify your response.
______________
Answer:
Negative
Explanation:
Scientific notation is used to express very small or very large numbers.
Very small numbers are written in scientific notation using negative exponents.
Very large numbers are written in scientific notation using positive exponents.
Since a ladybug is very small, we would use the very small scientific notation, which uses negative exponents.
Physical Science – Scientific Notation with Negative Powers of 10 – Page No. 50
The table shows the length of the radii of several very small or very large items. Complete the table.
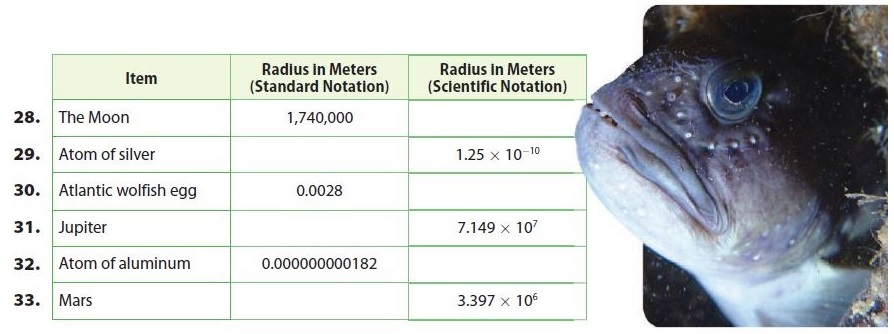
Question 28.
Type below:
______________
Answer:
1.74 × (10)6
Explanation:
The moon = 1,740,000
Move the decimal left 6 places
1.74 × (10)6
Question 29.
Type below:
______________
Answer:
1.25e-10
Explanation:
1.25 × (10)-10
Move the decimal left 10 places
1.25e-10
Question 30.
Type below:
______________
Answer:
2.8 × (10)3
Explanation:
0.0028
Move the decimal left 3 places
2.8 × (10)3
Question 31.
Type below:
______________
Answer:
71490000
Explanation:
7.149 × (10)7
Move the decimal left 7 places
71490000
Question 32.
Type below:
______________
Answer:
1.82 × (10)-10
Explanation:
0.000000000182
Move the decimal right 10 places
1.82 × (10)-10
Question 33.
Type below:
______________
Answer:
3397000
Explanation:
3.397 × (10)6
Move the decimal left 6 places
3397000
Question 34.
List the items in the table in order from the smallest to the largest.
Type below:
______________
Answer:
1.82 × (10)-10
1.25 × (10)-10
2.8 × (10)3
1.74 × (10)6
3.397 × (10)6
7.149 × (10)7
H.O.T.
Focus on Higher Order Thinking
Question 35.
Analyze Relationships
Write the following diameters from least to greatest. 1.5 × 10-2m ; 1.2 × 102 m ; 5.85 × 10-3 m ; 2.3 × 10-2 m ; 9.6 × 10-1 m.
Type below:
______________
Answer:
5.85 × 10-3 m, 1.5 × 10-2m, 2.3 × 10-2 m, 9.6 × 10-1 m, 1.2 × 102 m
Explanation:
1.5 × 10-2m = 0.015
1.2 × 102 m = 120
5.85 × 10-3 m = 0.00585
2.3 × 10-2 m = 0.023
9.6 × 10-1 m = 0.96
0.00585, 0.015, 0.023, 0.96, 120
Question 36.
Critique Reasoning
Jerod’s friend Al had the following homework problem:
Express 5.6 × 10-7 in standard form.
Al wrote 56,000,000. How can Jerod explain Al’s error and how to correct it?
Type below:
______________
Answer:
Explanation:
5.6 × 10-7 in
0.000000056
Al wrote 56,000,000. AI wrote the zeroes to the right side of the 56 which is not correct. As the exponent of 10 is negative zero’s need to add to the left of the number.
Question 37.
Make a Conjecture
Two numbers are written in scientific notation. The number with a positive exponent is divided by the number with a negative exponent. Describe the result. Explain your answer.
Type below:
______________
Answer:
When the division is performed, the denominator exponent is subtracted from the numerator exponent. Subtracting a negative value from the numerator exponent will increase its value.
Guided Practice – Operations with Scientific Notation – Page No. 54
Add or subtract. Write your answer in scientific notation.
Question 1.
4.2 × 106 + 2.25 × 105 + 2.8 × 106
4.2 × 106 + ? × 10 ? + 2.8 × 106
4.2 + ? + ?
? × 10?
Type below:
______________
Answer:
4.2 × 106 + 0.225 × 10 × 105 + 2.8 × 106
Rewrite 2.25 = 0.225 × 10
(4.2 + 0.225 + 2.8) × 106
7.225 × 106
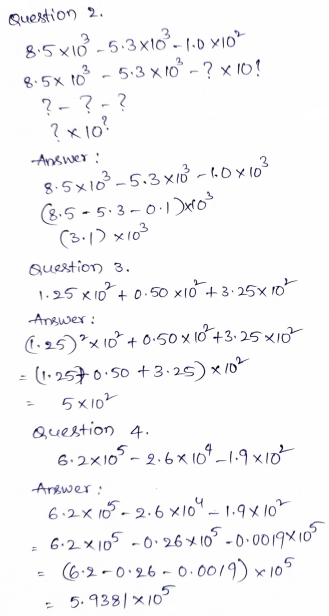
Multiply or divide. Write your answer in scientific notation.
Question 5.
(1.8 × 109)(6.7 × 1012)
Type below:
______________
Answer:
12.06 × 1021
Explanation:
(1.8 × 109)(6.7 × 1012)
1.8 × 6.7 = 12.06
109+12 = 1021
12.06 × 1021
Question 6.
\(\frac { { 3.46×10 }^{ 17 } }{ { 2×10 }^{ 9 } } \)
Type below:
______________
Answer:
1.73 × 108
Explanation:
3.46/2 = 1.73
1017/109 = 1017-9 = 108
1.73 × 108
Question 7.
(5 × 1012)(3.38 × 106)
Type below:
______________
Answer:
16.9 × 1018
Explanation:
(5 × 1012)(3.38 × 106)
5 × 3.38 = 16.9
106+12 = 1018
16.9 × 1018
Question 8.
\(\frac { { 8.4×10 }^{ 21 } }{ { 4.2×10 }^{ 14 } } \)
Type below:
______________
Answer:
2 × 107
Explanation:
8.4/4.2 = 2
1021/1014 = 1021-14 = 107
2 × 107
Write each number using calculator notation.
Question 9.
3.6 × 1011
Type below:
______________
Answer:
3.6e11
Question 10.
7.25 × 10-5
Type below:
______________
Answer:
7.25e-5
Question 11.
8 × 10-1
Type below:
______________
Answer:
8e-1
Write each number using scientific notation.
Question 12.
7.6E − 4
Type below:
______________
Answer:
7.6 × 10-4
Question 13.
1.2E16
Type below:
______________
Answer:
1.2 × 1016
Question 14.
9E1
Type below:
______________
Answer:
9 × 101
ESSENTIAL QUESTION CHECK-IN
Question 15.
How do you add, subtract, multiply, and divide numbers written in scientific notation?
Type below:
______________
Answer:
Numbers with exponents can be added and subtracted only when they have the same base and exponent.
To multiply two numbers in scientific notation, multiply their coefficients and add their exponents.
To divide two numbers in scientific notation, divide their coefficients, and subtract their exponents.
Independent Practice – Operations with Scientific Notation – Page No. 55
Question 16.
An adult blue whale can eat 4.0 × 107 krill in a day. At that rate, how many krill can an adult blue whale eat in 3.65 × 102 days?
Type below:
______________
Answer:
14.6 × 109
Explanation:
(4.0 × 107 )(3.65 × 102 )
4.0 × 3.65 = 14.6
107+2 = 109
14.6 × 109
Question 17.
A newborn baby has about 26,000,000,000 cells. An adult has about 4.94 × 1013 cells. How many times as many cells does an adult have than a newborn? Write your answer in scientific notation.
Type below:
______________
Answer:
1.9 × 103
Explanation:
26,000,000,000 = 2.6 × 1010
4.94 × 1013
(4.94 × 1013 )/(2.6 × 1010 )
1.9 × 103
Represent Real-World Problems
The table shows the number of tons of waste generated and recovered (recycled) in 2010.

Question 18.
What is the total amount of paper, glass, and plastic waste generated?
Type below:
______________
Answer:
11.388 × 107
Explanation:
7.131 × 107 + 1.153 × 107 + 3.104 × 107
11.388 × 107
Question 19.
What is the total amount of paper, glass, and plastic waste recovered?
Type below:
______________
Answer:
5.025 × 107
Explanation:
4.457 × 107 + 0.313 × 107 + 0.255 × 107
5.025 × 107
Question 20.
What is the total amount of paper, glass, and plastic waste not recovered?
Type below:
______________
Answer:
6.363 × 107
Explanation:
(11.388 × 107 ) – (5.025 × 107)
6.363 × 107
Question 21.
Which type of waste has the lowest recovery ratio?
Type below:
______________
Answer:
Plastics
Explanation:
7.131 × 107 – 4.457 × 107 = 2.674 × 107
1.153 × 107 – 0.313 × 107 = 0.84 × 107
3.104 × 107 – 0.255 × 107 = 2.849 × 107
Plastics has the lowest recovery ratio
Social Studies
The table shows the approximate populations of three countries.

Question 22.
How many more people live in France than in Australia?
Type below:
______________
Answer:
4.33 × 107
Explanation:
(6.48 × 107 ) – (2.15× 107)
4.33 × 107
Question 23.
The area of Australia is 2.95 × 106 square miles. What is the approximate average number of people per square mile in Australia?
Type below:
______________
Answer:
About 7 people per square mile
Explanation:
2.95 × 106 square miles = (2.15× 107)
1 square mile = (2.15× 107)/(2.95 × 106) = 7.288
Question 24.
How many times greater is the population of China than the population of France? Write your answer in standard notation.
Type below:
______________
Answer:
20.52; there are about 20 people in china for every 1 person in France.
Question 25.
Mia is 7.01568 × 106 minutes old. Convert her age to more appropriate units using years, months, and days. Assume each month to have 30.5 days.
Type below:
______________
Answer:
13 years 3 months 22.5 days
Explanation:
7.01568 × 106 minutes
(7.01568 × 106 minutes) ÷ (6 × 101)(2.4 × 101)(1.2 × 101)(3.05 × 101)
= (1.331 × 101)
= 13 years 3 months 22.5 days
Operations with Scientific Notation – Page No. 56
Question 26.
Courtney takes 2.4 × 104 steps during her long-distance run. Each step covers an average of 810 mm. What total distance (in mm) did Courtney cover during her run? Write your answer in scientific notation. Then convert the distance to the more appropriate unit kilometers. Write that answer in standard form.
______ km
Answer:
19.4 km
Explanation:
Courtney takes 2.4 × 104 steps during her long-distance run. Each step covers an average of 810 mm.
(2.4 × 104 steps) × 810mm
(2.4 × 104 ) × (8.1 × 102 )
The total distance covered = (19.44 × 106 )
Convert to unit kilometers:
(19.44 × 106 ) × (1 × 10-6 )
(1.94 × 101 )
19.4 km
Question 27.
Social Studies
The U.S. public debt as of October 2010 was $9.06 × 1012. What was the average U.S. public debt per American if the population in 2010 was 3.08 × 108 people?
$ _______
Answer:
$29,400 per American
Explanation:
($9.06 × 1012.)/(3.08 × 108 )
($2.94 × 104.) = $29,400 per American
H.O.T.
Focus on Higher Order Thinking
Question 28.
Communicate Mathematical Ideas
How is multiplying and dividing numbers in scientific notation different from adding and subtracting numbers in scientific notation?
Type below:
______________
Answer:
When you multiply or divide in scientific notation, you just add or subtract the exponents. When you add or subtract in scientific notation, you have to make the exponents the same before you can do anything else.
Question 29.
Explain the Error
A student found the product of 8 × 106 and 5 × 109 to be 4 × 1015. What is the error? What is the correct product?
Type below:
______________
Answer:
The error student makes is he multiplies the terms instead of adding.
Explanation:
product of 8 × 106 and 5 × 109
40 × 1015
4 × 1016
The student missed the 10 while multiplying the product of 8 × 106 and 5 × 109
Question 30.
Communicate Mathematical Ideas
Describe a procedure that can be used to simplify \(\frac { { (4.87×10 }^{ 12 }) – { (7×10 }^{ 10 }) }{ { (3×10 }^{ 7 })-{ (6.1×10 }^{ 8 }) } \). Write the expression in scientific notation in simplified form.
Type below:
______________
Answer:
\(\frac { { (4.87×10 }^{ 12 }) – { (7×10 }^{ 10 }) }{ { (3×10 }^{ 7 })-{ (6.1×10 }^{ 8 }) } \)
\(\frac { { (487×10 }^{ 10 }) – { (7×10 }^{ 10 }) }{ { (3×10 }^{ 7 })-{ (61×10 }^{ 7 }) } \)
(480 × 1010 )/(64 × 107 )
7.50 × 10³
2.1 Integer Exponents – Model Quiz – Page No. 57
Find the value of each power.
Question 1.
3-4
\(\frac{□}{□}\)
Answer:
\(\frac{1}{81}\)
Explanation:
Base = 3
Exponent = 4
3-4 = (1/3)4 = 1/81
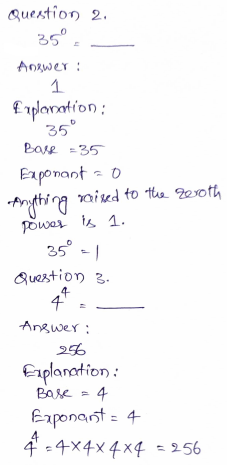
Use the properties of exponents to write an equivalent expression.
Question 4.
83 ⋅ 87
Type below:
____________
Answer:
810
Explanation:
83 ⋅ 87
83+7
810
Question 5.
\(\frac { 12^{ 6 } }{ 12^{ 2 } } \)
Type below:
____________
Answer:
124
Explanation:
126 ÷ 122
126-2
124
Question 6.
(103)5
Type below:
____________
Answer:
108
Explanation:
(103)5
(103+5)
(108)
2.2 Scientific Notation with Positive Powers of 10
Convert each number to scientific notation or standard notation.
Question 7.
2,000
Type below:
____________
Answer:
2 × (103)
Explanation:
2 × 1,000
Move the decimal left 3 places
2 × (103)
Question 8.
91,007,500
Type below:
____________
Answer:
9.10075 × (107)
Explanation:
91,007,500
Move the decimal left 7 places
9.10075 × (107)
Question 9.
1.0395 × 109
Type below:
____________
Answer:
1039500000
Explanation:
1.0395 × 109
Move the decimal right 9 places
1039500000
Question 10.
4 × 102
Type below:
____________
Answer:
400
Explanation:
4 × 102
Move the decimal right 2 places
400
2.3 Scientific Notation with Negative Powers of 10
Convert each number to scientific notation or standard notation.
Question 11.
0.02
Type below:
____________
Answer:
2 × 10-2
Explanation:
0.02
Move the decimal right 2 places
2 × 10-2
Question 12.
0.000701
Type below:
____________
Answer:
7.01 × 10-4
Explanation:
0.000701
Move the decimal right 4 places
7.01 × 10-4
Question 13.
8.9 × 10-5
Type below:
____________
Answer:
0.000089
Explanation:
8.9 × 10-5
Move the decimal left 5 places
0.000089
Question 14.
4.41 × 10-2
Type below:
____________
Answer:
0.0441
Explanation:
4.41 × 10-2
Move the decimal left 2 places
0.0441
2.4 Operations with Scientific Notation
Perform the operation. Write your answer in scientific notation.
Question 15.
7 × 106 − 5.3 × 106
Type below:
____________
Answer:
1.7 × 106
Explanation:
7 × 106 − 5.3 × 106
(7 – 5.3) × 106
1.7 × 106
Question 16.
3.4 × 104 + 7.1 × 105
Type below:
____________
Answer:
7.44 × 104
Explanation:
3.4 × 104 + 7.1 × 105
0.34 × 105 + 7.1 × 105
(0.34 + 7.1) × 105
7.44 × 105
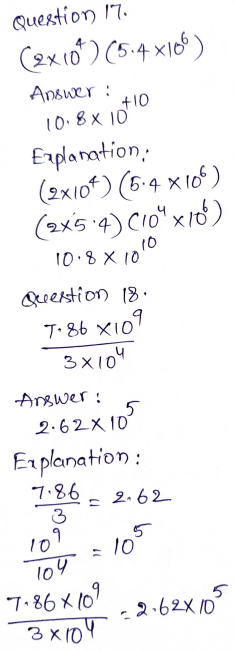
Question 19.
Neptune’s average distance from the Sun is 4.503×109 km. Mercury’s average distance from the Sun is 5.791 × 107 km. About how many times farther from the Sun is Neptune than Mercury? Write your answer in scientific notation.
Type below:
____________
Answer:
(0.7776 × 102 km) = 77.76 times
Explanation:
Neptune’s average distance from the sun is 4.503×109 km and Mercury’s is 5.791 × 107 km
(4.503×109 km)/(5.791 × 107 km)
(0.7776 × 109-7 km)
(0.7776 × 102 km)
77.76 times
Essential Question
Question 20.
How is scientific notation used in the real world?
Type below:
____________
Answer:
Scientific notation is used to write very large or very small numbers using less digits.
Selected Response – Mixed Review – Page No. 58
Question 1.
Which of the following is equivalent to 6-3?
Options:
a. 216
b. \(\frac{1}{216}\)
c. −\(\frac{1}{216}\)
d. -216
Answer:
b. \(\frac{1}{216}\)
Explanation:
Base = 6
Exponent = 3
63 = (1/6)3 = 1/216
Question 2.
About 786,700,000 passengers traveled by plane in the United States in 2010. What is this number written in scientific notation?
Options:
a. 7,867 × 105 passengers
b. 7.867 × 102 passengers
c. 7.867 × 108 passengers
d. 7.867 × 109 passengers
Answer:
c. 7.867 × 108 passengers
Explanation:
786,700,000
Move the decimal left 8 places
7.867 × 108 passengers
Question 3.
In 2011, the population of Mali was about 1.584 × 107 people. What is this number written in standard notation?
Options:
a. 1.584 people
b. 1,584 people
c. 15,840,000 people
d. 158,400,000 people
Answer:
c. 15,840,000 people
Explanation:
1.584 × 107
Move the decimal right 7 places
15,840,000 people
Question 4.
The square root of a number is between 7 and 8. Which could be the number?
Options:
a. 72
b. 83
c. 51
d. 66
Answer:
c. 51
Explanation:
7²= 49
8²=64
(49+64)/2
56.5
Question 5.
Each entry-level account executive in a large company makes an annual salary of $3.48 × 104. If there are 5.2 × 102 account executives in the company, how much do they make in all?
Options:
a. $6.69 × 101
b. $3.428 × 104
c. $3.532 × 104
d. $1.8096 × 107
Answer:
d. $1.8096 × 107
Explanation:
Each entry-level account executive in a large company makes an annual salary of $3.48 × 104. If there are 5.2 × 102 account executives in the company,
($3.48 × 104)( 5.2 × 102)
$1.8096 × 107
Question 6.
Place the numbers in order from least to greatest.
0.24,4 × 10-2, 0.042, 2 × 10-4, 0.004
Options:
a. 2 × 10-4, 4 × 10-2, 0.004, 0.042, 0.24
b. 0.004, 2 × 10-4, 0.042, 4 × 10-2, 0.24
c. 0.004, 2 × 10-4, 4 × 10-2, 0.042, 0.24
d. 2 × 10-4, 0.004, 4 × 10-2, 0.042, 0.24
Answer:
d. 2 × 10-4, 0.004, 4 × 10-2, 0.042, 0.24
Explanation:
2 × 10-4 = 0.0002
4 × 10-2 = 0.04
Question 7.
Guillermo is 5 \(\frac{5}{6}\) feet tall. What is this number of feet written as a decimal?
Options:
a. 5.7 feet
b. 5.\(\bar{7}\) feet
c. 5.83 feet
d. 5.8\(\bar{3}\) feet
Answer:
c. 5.83 feet
Question 8.
Human hair has a width of about 6.5 × 10-5 meters. What is this width written in standard notation?
Options:
a. 0.00000065 meter
b. 0.0000065 meter
c. 0.000065 meter
d. 0.00065 meter
Answer:
c. 0.000065 meter
Explanation:
6.5 × 10-5 meter = 0.000065
Mini-Task
Question 9.
Consider the following numbers: 7000, 700, 70, 0.7, 0.07, 0.007
a. Write the numbers in scientific notation.
Type below:
_____________
Answer:
7000 = 7 × 10³
700 = 7 × 10²
70 = 7 × 10¹
0.7 = 7 × 10¯¹
0.07 = 7 × 10¯²
0.007 = 7 × 10¯³
Question 9.
b. Look for a pattern in the given list and the list in scientific notation. Which numbers are missing from the lists?
Type below:
_____________
Answer:
In the given list the decimal is moving to the left by one place. From the scientific notation, numbers are decreasing by 10. The number missing is 7
Question 9.
c. Make a conjecture about the missing numbers.
Type below:
_____________
Answer:
The numbers will continue to decrease by 10 in the given list.
Conclusion:
We wish the information provided in the Go Math Grade 8 Answer Key Chapter 2 Exponents and Scientific Notation for all the students. Go through the solved examples to have a complete grip on the subject and also on the way of solving each problem. Go Math Grade 8 Chapter 2 Exponents and Scientific Notation Key will help the students to score the highest marks in the exam.
