A cuboid is a solid rectangular figure with three dimensions such as length, breadth, and height. To find the lateral surface area of a cuboid we have to add the length and breadth of the cuboid and multiply the sum with the height of the given solid figure. Here you can find the details of the solid figures like the lateral surface area of cuboid definition, the formula of LSA, How to find the lateral surface area of a cuboid, and examples of LSA of a cuboid.
See More:
Lateral Surface Area of a Cuboid – Definition
A cuboid has six faces, eight vertices, and twelve edges similar to the cube. The sum of surface areas of all sides except the top and bottom face of a solid is defined as the lateral surface area of a solid. The metric units of the Lateral Surface Area (LSA) of a Cuboid are Square units, square centimeters, square meters, square inches, etc.
Formula for finding Lateral Surface Area of a Cuboid
Area of the room = sum of the vertical faces
A = 2(l + b)h
where,
A = Area of the cuboid
l = length
b = base
h = height
How to Find Lateral Surface Area of a Cuboid?
The lateral surface area of a cuboid is nothing but the area of each surface of the cuboid. There are some steps to calculate the surface area of a cuboid. Go through the following steps and solve the problems.
Step 1: Check the dimensions of the cuboid.
Step 2: If the units of the dimensions are not the same then you have it into the same units.
Step 3: Once the dimensions are the same then use the formula of the lateral surface of the cuboid
Step 4: After that express the obtained value and write the units of the answer.
LSA of a Cuboid Examples
Example 1.
Find the lateral surface and total surface area of a cuboid of length 8 cm, breadth 4 cm, and height 2 cm.
Solution:
Given that
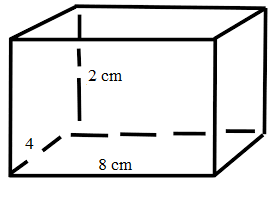
length (l) = 8 cm
Breadth (b) = 4 cm
Height (h) = 2 cm
The lateral surface area of the cuboid = 2(lh+bh)=2h(l + b)
Lateral surface area =2(2)(8+4)
= 4(12)
= 48 cm².
Therefore the lateral surface area of a cuboid = 48 cm²
Example 2.
Rahul has a rice container with dimensions of length 8 cm, breadth 12 cm, and height 14 cm. Find the lateral surface area of a rice container
Solution:
Given that
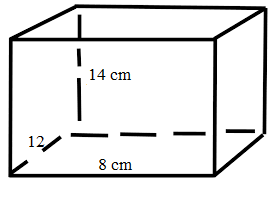
Length of a rice container = 8cm
Breadth of a rice container = 12 cm
Height of a rice container= 14 cm
Know we have to find out the lateral surface of the area of a rice container
We know that
The lateral surface area of the cuboid = 2(lh+bh)=2h(l + b)
The rice container is in the shape of a cuboid.
The lateral surface area of a rice container = 2 × 14 (8 + 12)
= 28(20)
= 560 cm²
Therefore, The lateral surface area of a rice container is 560 cm²
Example 3.
The dimensions of a cuboid are length 12 cm breadth 16 cm and height 15 cm. Find the lateral surface area of a cuboid.
Solution:
Given that
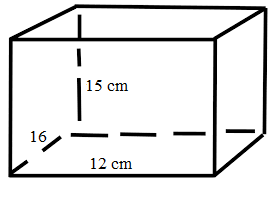
Length of a cuboid = 12 cm
Breadth of a cuboid = 16 cm
Height of a cuboid = 15 cm
The lateral surface area of the cuboid = 2(lh+bh)=2h(l + b)
= 2 × 15(12 + 16)
= 30(28)
= 840 cm²
Therefore The lateral surface area of the cuboid = 840 cm²
Example 4.
The dimensions of a cubical room are 4 m × 3 m × 6 m. The room has two doors each measuring 5 m by 1 m and four windows each measuring 1 m by 1 m. What will be the cost of plastering the four walls and the ceiling at Rs 35 per m²
Solution:
The total area of the four walls = Lateral surface area of the cuboid
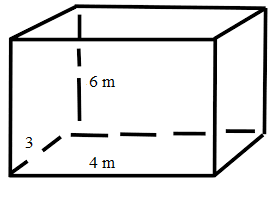
= 2(l + b)h
= 2(4 + 3) × 6
= 2(7) × 6m2
= 84 m².
The area of the ceiling = l × b
= 4 × 3
= 12 m²
The sum of the areas of the two doors and the four windows
5(5 × 1) m² + 6(1 × 1) m²
= 31 m²
Therefore, the total area to be plastered = lateral surface area + area of the ceiling – sum of the areas of the doors and the four windows
= (84 + 12 – 31) m²
= 65 m²
Therefore, the cost of plastering = 65× Rs. 35
= Rs. 2275
Example 5.
Find the lateral surface and total surface area of a cuboid of length 3 cm, breadth 13 cm and height 24 cm.
Solution:
Given that
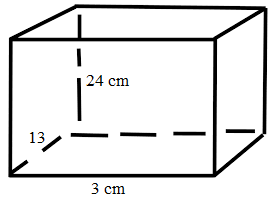
length (l) = 3 cm
Breadth (b) = 13 cm
Height (h) = 24 cm
The lateral surface area of the cuboid = 2(lh+bh)=2h(l + b)
Lateral surface area =2(24)(3 + 13)
= 48(16)
= 768 cm².
Therefore the lateral surface area of a cuboid = 768 cm²
FAQs on Lateral Surface Area of a Cuboid
1. What is the formula for the lateral surface area?
The lateral surface area of an object is equal to the surface area minus the area of the bases of the object.
2. How do you work out the surface area of a cuboid?
The surface area of cuboid = 2(lb + bh + lh),
where ‘l’ is the base length of the cuboid,
‘b’ is the base width of the cuboid, and
‘h’ is the height of the cuboid.
3. How many lateral faces does a cuboid have?
The four faces which are adjacent to the base are called the lateral faces of the cuboid.