The line of symmetry is the axis or imaginary line that passes through the center of an object and divides it into identical halves. If we cut an equilateral triangle into two halves, then it forms two right-angled triangles. Similarly, rectangle, square, circle are examples of a line of symmetry. The line of symmetry is also called an axis of symmetry. Also, it is named a mirror line where it forms two reflections of an image. A basic definition of a line of symmetry is it divides an object into two halves.
Types of Lines of Symmetry
There are mainly two types considered in Lines of Symmetry concepts. They are
1. Vertical Line of Symmetry
2. Horizontal Line of Symmetry
Vertical Line of Symmetry: If the axis of the shape cuts it into two equal halves vertically then it is called a Vertical Line of Symmetry. The mirror image of the one half appears in a vertical or straight standing position. Examples for vertical Line of Symmetry are H, M, A, U, O, W, V, Y, T.
Horizontal Line of Symmetry: If the axis of the shape cuts it into two equal halves horizontally, then it is called as Horizontal Line of Symmetry. The mirror image of the one half appears as the other similar half. Examples of Horizontal Line of Symmetry are C, B, H, E.
Three Lines of Symmetry: An equilateral triangle is an example of three lines of symmetry. This is symmetrical along its three medians.
Four Lines of Symmetry: A square is an example of Four Lines of Symmetry. The symmetrical lines are two along the diagonals and two along with the midpoints of the opposite sides.
Five Lines of Symmetry: A regular pentagon is an example of Five Lines of Symmetry. The symmetrical lines are joining a vertex to the mid-point of the opposite side.
Six Lines of Symmetry: A regular hexagon is an example of Six Lines of Symmetry. The symmetrical lines are 3 joining the opposite vertices and 3 joining the mid-points of the opposite sides.
Infinite Lines of Symmetry: A circle is an example of Infinite Lines of Symmetry. It has infinite or no lines of symmetry. It is symmetrical along all its diameters.
Line of Symmetry Examples
Check out some of the examples of Line of Symmetry and learn completely with clear details.
1. Line segment:
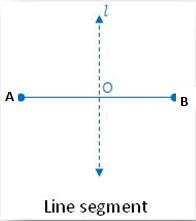
From the figure, there is one line of symmetry. line of symmetry of a Line segment passes through its center. There may infinite line passes through the line segment and forms different angles. But we only consider a line as a line of symmetry that cuts the line segment into two equal halves. The Line segment AB is symmetric along the perpendicular bisector l.
2. An angle:
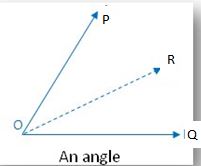
From the figure, there is one line of symmetry. An angle measures the amount of ‘turning’ between two straight lines that meet at a point. The figure is symmetric along the angle bisector OC.
3. An isosceles triangle:
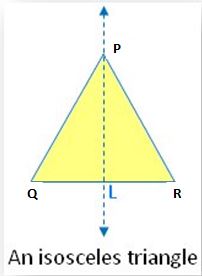
From the figure, there is one line of symmetry. The isosceles triangle figure is symmetric along the bisector of the vertical angle. The Median PL. If the isosceles triangle is also an equilateral triangle, then it has three lines of symmetry. An isosceles triangle has exactly two sides of equal length. Therefore, it has only 1 line of symmetry that passes from the vertex between the two sides of equal length to the midpoint of the side opposite that vertex.
4. Semi-circle:
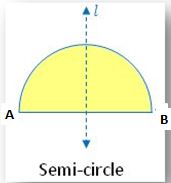
From the figure, there is one line of symmetry. The Semi-circle figure is symmetric along the perpendicular bisector l. of the diameter AB. A semi-circle does not have any rotational symmetry.
5. Kite:
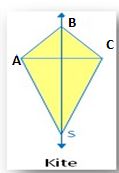
From the figure, there is one line of symmetry. The Kite is symmetric along with the diagonal BS. A kite is a quadrilateral with two different pairs of adjacent sides that are equal in length and also have only one line of symmetry.
6. Isosceles trapezium:
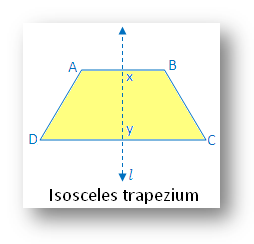
From the figure, there is one line of symmetry. The Isosceles trapezium figure is symmetric along the line l joining the midpoints of two parallel sides AB and DC. The isosceles trapezium is a convex quadrilateral consists a pair of non-parallel sides that are equal and another pair of sides is parallel but not equal.
7. Rectangle:
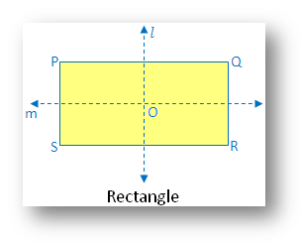
From the figure, there are two lines of symmetry. The Rectangle figure is symmetric along the lines l and m joining the midpoints of opposite sides. There are 2 symmetry lines of a rectangle which are from its length and breadth. They cut the rectangle into two equal halves. They appear mirror to each other.
8. Rhombus:
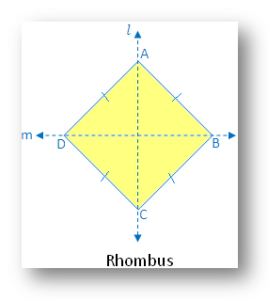
From the figure, there are two lines of symmetry. The Rhombus figure is symmetric along the diagonals AC and BD of the figure. Both the lines of symmetry in a rhombus are from its diagonals. So, it can also say the rhombus lines of symmetry are both diagonals.
Lines of Symmetry in Alphabets
Have a look at the letters that have the line of symmetry.
One Line of symmetry: The letters consist of One line of symmetry are A B C D E K M T U V W Y.
Vertical Line of symmetry: The letters consist of a Vertical line of symmetry is A M T U V W Y.
Horizontal Line of symmetry: The letters consist of a Horizontal line of symmetry is B C D E K.
Two Lines of Symmetry: The letters consist of Two lines of symmetry are H I X. These are having both horizontal and vertical lines of symmetry.
No Lines of Symmetry: The letters consist of No lines of symmetry are F G J L N P Q R S Z. These have neither horizontal nor vertical lines of symmetry.
Infinite Lines of Symmetry: The letter having Infinite lines of symmetry is O.
