In this article, you can know about the Midpoint Theorem which is invented by Rene Descartes, the famous mathematician. In geometry, the midpoint theorem benefits to find the missing values of the sides of the triangle. The midpoint theorem is one of the important theorems in the concept of geometry.
The midpoint theorem deals with the properties of triangles. Students can learn about the definition, statement, formula, proof of the Midpoint Theorem, and examples to find the coordinates of the defined points.
Related Articles:
Midpoint Theorem – Definition
The term midpoint means the ‘center’ of something, it is the midway between the two endpoints. The midpoint theorem expresses that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side of the triangle. A midpoint generally means a point on a line segment that has an equal distance from both endpoints and bisects the line segment.
Statement of Midpoint Theorem
The midpoint theorem states that “The line segment in a triangle joining the midpoint of two sides of the triangle is said to be parallel to its third side of the triangle and is also half of the length of the third side.”
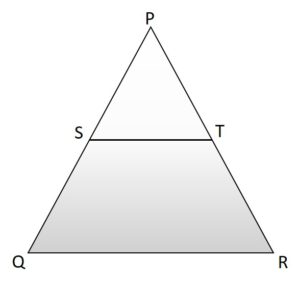
Proof of Midpoint Theorem
Consider the triangle PQR, as shown in the above figure
Let S and T be the midpoint of the sides PQ and PR. Now, the line ST is said to be parallel to the side QR, where the ST is half of the side QR, i.e.,
ST ∥ QR
ST = (½ × QR)
Now, if you consider the below figure, it is an extended version of the above figure provided.
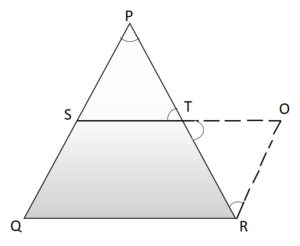
Construction:
Extend the line segment ST and produce it to point O such that, OT = ST.
In a triangle, PST and TOR,
TR = PT – – (given)
∠RTO = ∠PTD (vertically opposite angles)
∠SPT = ∠TRO (alternate angles)
By ASA congruence criterion,
△TOR ≅ △PST
Therefore,
∠ROT = ∠PST { by c.p.c.t.c}
∠ORT = ∠SPT { by c.p.c.t.c}
and RO = PS { by c.p.c.t.c}
∠ROT and ∠PSE are the alternate interior angles.
Assume OR and PQ as two lines that are intersected by the transversal SO.
Similarly, ∠ORT and ∠SPT are the alternate interior angles.
Let us again assume that OR and PQ are the two lines that are intersected by the transversal PR.
Therefore, OR ∥ PQ
So, OR ∥ SQ
and OR = SQ (since SQ = SP, it is proved that OR = PS)
Thus, OSQR forms a parallelogram.
By the properties of a parallelogram, we can write
QR ∥ ST
and QR = ST
ST ∥ QR
and ST = (½ × QR)
Hence, the midpoint theorem is proved.
Midpoint Theorem Formula
In geometry, the midpoint theorem describes the midpoint of the line segment. It specifies the coordinate points of the midpoint of the line segment and can be identified by taking the average of the coordinates of the given endpoints. The formula for midpoint is used to identify the midpoint between the two given points.
If (x1, y1) and (x2, y2) are the coordinates of two given endpoints, then the midpoint formula is as follows
Midpoint (x,y) = [ (x1+x2)/2, (y1+y2)/2 ]
Here, x1 and x2 are coordinates of the x-axis, and y1 and y2 are the coordinates of the y-axis.
For example, to find the midpoint of (x,y,z) then the midpoint formula is
(x,y,z) = [ (x1+x2)/2, (y1+y2)/2 , (z1+z2)/2 ]
The coordinates are (x1,y1,z1), (x2,y2,z2).
Examples of Midpoint Theorem
Example 1:
In triangle PQR, the midpoints of PQ, RP, QR are S, T, and U respectively. Find the value of ST, if the value of QR = 12 cm.

Solution:
Given QR = 14 cm
If S is the midpoint of PQ and T is the midpoint of PR then using the midpoint theorem
ST = (½ × QR)
Substituting the value of QR,
ST = (½ × 12)
ST = 6 cm.
Therefore, the value of ST is 6cm.
Example 2:
How do you solve a problem such that the point (1,4) is the midpoint of (2,-4), and at what point is the second coordinate?
Solution:
The first coordinates are (2,-4).
Let us assume that the other coordinates are (m,n).
Now, the formula for midpoint is
(x,y) = [ (x1+x2)/2, (y1+y2)/2 ]
Substitute the above given values,
We get,
(1,4) = [(2+m)/2,(-4+n)/2]
⇒ (2+m)/2 = 1 and (-4+n)/2 = 4
⇒ m= 0 and n= 12.
Therefore, the second point has coordinates (0,12).
Example 3:
Find the coordinates of the center of the circle. The endpoints of the triangle are given as (6, 2), and (2, 4).
Solution:
Given coordinates of the triangle are
(6, 2) = (x1, y1) and (2, 4) = (x2, y2)
Coordinates of the center of the circle (x,y) = [ (x1+x2)/2, (y1+y2)/2 ]
[ (x1+x2)/2, (y1+y2)/2 ]
= [ ( 6+2)/2, (2+4)/2 ]
= [ 8/2, 6/2 ]
= (4, 2)
Hence, the coordinates of the center of the circle are (4,2).
FAQs on Midpoint Theorem
1. what does the midpoint theorem says?
The midpoint defines that “the line segment drawn from the midpoint of two sides of the triangle is parallel to the third side of the triangle and it is half of the length of the third side of the triangle”.
2. Why is important to define a midpoint?
The midpoint formula applies when one is needed to find the exact center point between two defined points. A line segment has to use this formula to calculate the exact point that bisects a line segment defined by the two given points.
3. How to prove the midpoint theorem?
To prove the midpoint theorem, we use congruency rules. We draw a triangle outside to the given triangle so that it touches the sides of the triangle. Now, we prove that it is congruent to any one part of the triangle. Here, we use the CPCTC rules to prove the equality between the sides of the triangle.
4. What is the use of the midpoint theorem in everyday life?
The midpoint theorem is basically used to know the specific information regarding the length of the sides of the triangle.