All the students of 9th grade must know the properties of a parallelogram before proving the theorem on Opposite Angles of a Parallelogram is Equal. If you understand the theorem then you can solve different types of problems on properties of a parallelogram. We know that the opposite sides of a parallelogram are the same and parallel. Draw a transversal line from A to C in a parallelogram ABCD. The alternate angles of a parallelogram become equal and it is divided into two triangles.
Opposite Angles of a Parallelogram are Equal Theorem
Question: Prove that opposite angles of a parallelogram are equal?
Given: In a Parallelogram, the Opposite Angles Are Equal.
Proof:
Given: ABCD is a parallelogram, and ∠A, ∠B, ∠C, ∠D are the four angles.
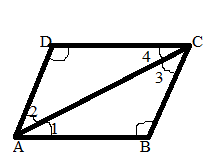
To Prove that:
∠A =∠C and ∠B=∠D
Let us assume that ABCD is a parallelogram. Now compare triangles ABC, and CDA. Here we have
AC=AC (common sides)
∠1=∠4 (alternate interior angles)
∠2=∠3 (alternate interior angles).
Thus, by ASA, the two triangles are congruent, which means that ∠B=∠D. Similarly, we can show that ∠A=∠C. This proves that opposite angles in any parallelogram are equal.
Example:
If one angle of a parallelogram is 90°, show that all its angles will be equal to 90°.
Solution:
Consider the parallelogram ABCD in which ∠A is a right angle
We know that in any parallelogram, the opposite angles are equal.
Therefore ∠C=90°.
Also, in any parallelogram, the adjacent angles are supplementary.
This implies ∠B=180° – ∠ A=180° – 90° =90°.
Similarly
∠D=180° – ∠C=180° – 90° =90°.
Hence, ∠A=∠B=∠C=∠D = 90°.
All the angles in this parallelogram are equal to 90°.
We have proved that when one angle of a parallelogram is 90°, the parallelogram is a rectangle.
Also, See:
- Pair of Opposite Sides of a Parallelogram are Equal and Parallel
- Opposite Sides of a Parallelogram are Equal
Points to Remember:
1. Opposite sides of a parallelogram are congruent.
2. Opposite angles of a parallelogram are congruent.
3. Diagonals of a parallelogram bisect each other.
4. The consecutive angles are supplementary.
5. In a parallelogram if any of the angles is a right angle, then all the angles will be right angles.
FAQs on Opposite Angles of a Parallelogram are Equal
1. How do you find the opposite angles of a parallelogram?
There are 5 properties to be known to find the opposite angles of a parallelogram
1. Opposite sides are congruent
2. Opposite angles are congruent
3. Diagonals bisect each other.
4. Consecutive angles are supplementary
5. If any of the angles is a right angle, then all the angles will be right angles.
2. Are all angles of parallelogram equal?
A parallelogram must have equivalent opposite interior angles. The sum of all interior angles must have equal degrees. As the angles and are opposite interior angles they must be equivalent.
3. Is opposite angles are equal?
Opposite angles are non-adjacent angles formed by two intersecting lines. Opposite angles are congruent.