Primary school students should be familiar with the different types of lines to solve the most important geometry concepts of Math as it helps them in their higher education. In geometry, perpendicular lines are one of the important topics to understand all the concepts which involve lines. Every child has to know about the concept of lines and what it is made of? A line is simple which joins infinite points and has no starting or ending point.
Here, in this section, you can go through perpendicular lines, properties of perpendicular lines, types to draw perpendicular lines, and few perpendicular lines examples to know practically. So, let’s dive into this article and gain more about perpendicular lines.
What are Perpendicular Lines?
Perpendicular lines are the two distinct lines that intersect each other at 90° or at the right angle. In other words, a perpendicular line is a straight line that makes an angle of 90° with another line and 90° is also called a right angle. Now, look at the below figure to know how perpendicular lines meet at the right angle.
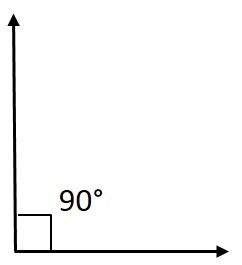
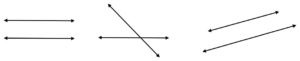
And, have a glance below to know some more examples that are not perpendicular lines. These lines are not meeting at any point nor intersect each other at any angle or at 90° so these lines are not called as perpendicular lines.
Perpendicular Line Symbol
Perpendicular lines are represented by a symbol ⊥. For suppose, if you have two lines m1 and m2 the two lines meet at the right angle of 90°, then they are perpendicular to each other. Symbolically, we represent the lines as m1 ⊥ m2 and we read as m1 is perpendicular to m2.
For example, let us represent the lines AB and CD, and the lines both intersect each other and the angle between them is a right angle.
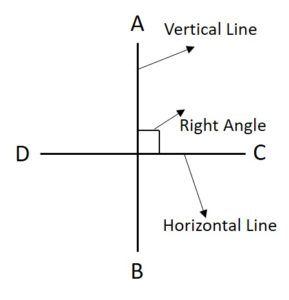
Here, line AB is intersecting with line CD at the right angle. So, both the lines are perpendicular lines. If two lines \(\overline{AB}\) and \(\overline{CD}\) are perpendicular to each other, we represent them as \(\overline{AB}\) ⊥ \(\overline{CD}\) and read them as \(\overline{AB}\) is perpendicular to \(\overline{CD}\).
Properties of Perpendicular Lines
We know how the perpendicular lines look. If there are two lines and their figure shape is “L”, the corresponding angle at the vertex is a right angle or 90°. Perpendicular lines meet and intersect each other but the lines can’t be perpendicular to each other always. The main properties of perpendicular lines are as follows:
- Perpendicular lines always meet or intersect each other at a right angle.
- The angle between perpendicular lines is always equal to 90°.
- If any two lines are perpendicular to the same line, then both the lines are parallel and never intersect each other.
Also, check:
Methods to Draw Perpendicular Lines
While we draw perpendicular lines students should know how many types are there to draw and what is the easiest method to draw quickly. All we need is a scale, compass, and protractor. There are various types to draw a perpendicular line in a certain method. So, the types to draw perpendicular lines are
- Using a Compass
- Using a Protractor
Real-Life Examples of Perpendicular Lines
If the students have observed clearly, there are plenty of examples in our real life that illustrates perpendicularity. They are:
- Hands of a clock when the time strikes to 3 o’Clock.
- The tiles of a kitchen and the corners of the wall intersect each other at a right angle.
- The intersection of roads at squares.
- The corners of your computer desk or table and the doors.
How to Construct Perpendicular Lines?
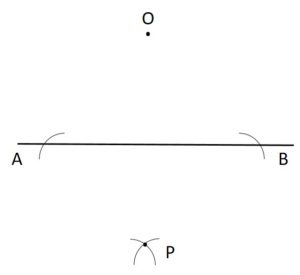
Follow the steps to draw a perpendicular line from the given point.
Step 1: Keep the compass on given point O. Draw an arc to the line on each side of the given point O. Do not adjust the width of the compass while drawing the second arc.
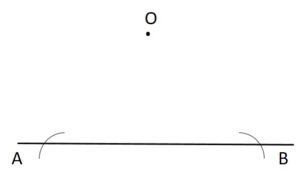
Step 2: Draw another arc on the opposite side of the line from the given point O, from each arc on the line. The two new arcs will intersect and label with another point (P).
Step 3: Use your ruler or scale to join the given point O and where the arcs intersect at point P.
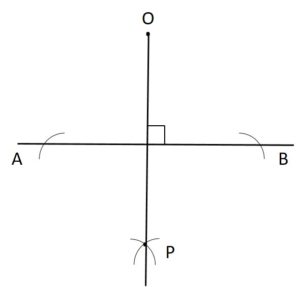
Now, AB is perpendicular to OP. We can also write as AB ⊥ OP.
Read Similar Articles: Construction of Perpendicular Lines by using a Protractor
Difference Between Perpendicular Lines and Parallel Lines
| Parallel Lines | Perpendicular Lines |
|---|---|
| Parallel lines are the lines that do not intersect at any point and always have the same distance between the lines. | Lines that intersect each other and forms a right angle or 90° are called perpendicular lines. |
| For example, in the steps of a straight ladder, the opposite sides of a rectangle are parallel lines. | The corner of two walls; the letter “L” is a real-time example of perpendicular lines |
| The symbol we use to represent two parallel lines: || | The symbol we use to represent two perpendicular lines: ⊥ |
Examples of Perpendicular Lines
Example 1:
In the following diagram, lines P and Q are perpendicular lines. If ∠a is 14 degrees less than ∠b, what is the measure of ∠a?
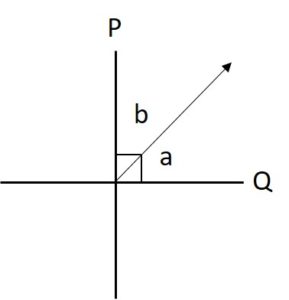
Solution:
Since we knew ∠a is 14° less than ∠b, we have ∠a = ∠b – 14°.
P and Q are perpendicular lines, we have ∠a + ∠b = 90°, now, substitute this equation in the first equation.
∠a + ∠b = 90°
∠b – 14° + ∠b = 90°
2∠b = 90°+ 14°
2∠b =104°
∠b = 52°
Now, find the measure of ∠a.
∠a = ∠b – 14°
∠a = 52° – 14° = 38°.
Thus, the measure of ∠a is 38°.
Example 2:
If one line passes through the points (-1, –3) and (–4, 6) and another line passes through the points (3, 5) and (–5, 1). Are these lines parallel lines or perpendicular lines?
Solution:
Slope of the equation is (y2 – y1) / (x2 – x1)
m1 = (6+3) / (-4+1) = 9/-3 = -2
m2 = (1-5) / (-5-3) = -4/-8 = 1/2
Since m1 ≠ m2 , hence, lines are not parallel.
Perpendicular lines formula is m1×m2= -1.
m1×m2= -2×(1/2)= -1.
Therefore, the given lines are perpendicular lines.
FAQ’s on Perpendicular Lines
1. What are perpendicular lines or angles?
The perpendicular lines can also be known as a right angle i.e., 90° that is formed when two lines intersect each other.
2. Does perpendicular lines touch each other?
Yes, the perpendicular lines touch each other. One of the properties says that the perpendicular lines intersect and touch each other.
3. What is the formula for perpendicular lines?
To know the slope of two lines we use the perpendicular line’s formula. The formula is defined as the product of two slopes m1 and m2 is -1. In mathematical terms, we express as m1×m2= -1 or m1 = -1/m2 .
