Problems on Finding Area of Triangle and Parallelogram are available here for free. So, the students who wish to solve different types of problems in the area can refer to our page and solve the questions in a simple method. Use the formulas of triangle and parallelogram to find the area of the given questions. Read the entire article and learn how to solve the problems on finding area of triangle and parallelogram.
Read More:
Finding Area of Triangle and Parallelogram Problems with Solutions
We have provided various types of questions on finding the area of triangles and parallelograms. This will help the students a lot to score good marks and also to improve their knowledge of the subject.
Example 1.
Find the Area of a triangle whose base is 6 cm and height is 8 cm.
Solution:
Given,
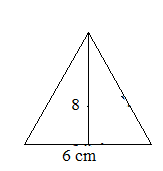
base = 6 cm
height = 8 cm
We know that,
Area of triangle = 1/2 × b × h
A = 1/2 × 6 × 8
A = 24 sq. cm
Thus the area of the triangle is 24 sq. cm.
Example 2.
What is the area of triangle and parallelogram if the base is 7 in and height 8 in?
Solution:
Given,
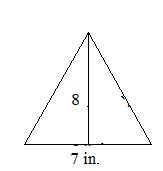
base = 7 in.
height = 8 in.
We know that,
Area of triangle = 1/2 × b × h
A = 1/2 × 7 × 8
A = 14 sq. in
Thus the area of the triangle is 14 sq. inches.
We know that,
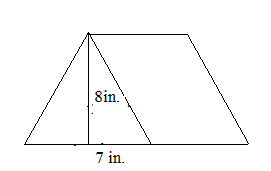
Area of parallelogram = bh
A = 7 × 8
A = 56 sq. in
Thus the area of a parallelogram is 56 sq. inches.
Example 3.
If the area of a parallelogram is 49 sq. meters and height is 7 meters. Find the base of the parallelogram?
Solution:
Given that,
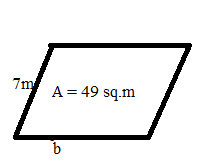
The area of a parallelogram is 49 sq. meters and
height is 7 meters
We know that,
Area of parallelogram = bh
49 = b × 7
b = 49/7
b = 7
Thus the base of the parallelogram is 7 meters.
Example 4.
What is the area of triangle and parallelogram if the base is 10 in and height 9 in?
Solution:
Given,
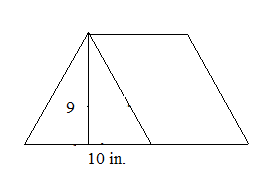
base = 10 in.
height = 9 in.
We know that,
Area of triangle = 1/2 × b × h
A = 1/2 × 10 × 9
A = 45 sq. in
Thus the area of the triangle is 45 sq. inches.
We know that,
Area of parallelogram = bh
A = 10 × 9
A = 90 sq. in
Thus the area of a parallelogram is 90 sq. inches.
Example 5.
Find the height of the triangle where the area is 100 sq. cm and the base is 50 cm?
Solution:
Given that,
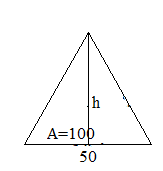
the area is 100 sq. cm and
the base is 50 cm
We know that,
Area of triangle = 1/2 × b × h
100 = 1/2 × 50 × h
100 = 25 h
h = 100/25
h = 4
Thus the height of the triangle is 4 cm.
Example 6.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 6cm, 8cm, and 10cm and the parallelogram stands on the base 8cm, find the height of the parallelogram?
Solution:
Perimeter of a triangle 2s = 6 + 8 + 10
2s = 24
s = 12
Area = √s(s – a)(s – b)(s – c)
Area = √12(12 – 6)(12 – 8)(12 – 10)
Area = 166
Area of Parallelogram = area of triangle
h × 8 = 166
h = 40.75
Height of the parallelogram is 40.75
Therefore h is 40.75 cm.
Example 7.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 16cm, 18cm, and 20cm and the parallelogram stands on the base 18cm, find the height of the parallelogram?
Solution:
Perimeter of a triangle 2s = 16 + 18 + 20
2s = 54
s = 27
Area = √s(s – a)(s – b)(s – c)
Area = √27(27 – 16)(27 – 18)(27 – 20)
Area = 3600
Area of Parallelogram = area of triangle
h × 18 = 3600
h = 200
Height of the parallelogram is 200
Thus the height of the parallelogram is 200 cm.
Example 8.
A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 24cm, 26cm, and 28cm, and the parallelogram stands on the base of 26. Find the height of the parallelogram?
Solution:
Area of the parallelogram = Area of the triangle
By using the area of parallelograms we can calculate the height of the parallelogram
Area of triangle = √s(s – a)(s – b)(s – c)
a, b, c are the sides of a triangle
S is the semi perimeter= half of the perimeter of the triangle
Let ABCD is a parallelogram and ABE is a triangle having a common base with parallelogram ABCD.
From ∆ABE
a = 28cm, b = 24cm, and c = 26cm
Semi perimeter (s) = perimeter/2
s = a + b + c/2
= 28 + 24 + 26/2 = 39
area of ∆ABE = √s(s – a)(s – b)(s – c)
√39(39 – 28)(39 – 24)(39 – 26)
= 289.23
Area of parallelogram ABCD = area of ∆ABE
Base × height = 289.23cm²
26cm² × height = 289.23cm²
Height = 11.12cm²
Thus the Height of the parallelogram is 11.12cm²
Example 9.
In the figure, ABCD is a Parallelogram N is a point BC such that BN: NC = 1: 4, DN produced meets AB produced at O. If the area of the triangle CNO = 40cm². Calculate the areas of the parallelogram ABCD and ∆CDN?
Solution:
Draw OP //BC which cuts DC produced at P.
Then CPOB is a parallelogram join CO.
Area of ∆BNO/∆CNO = BN/ND (both triangles have equal altitudes)
Area of ∆BNO/40cm² = 1/4
Area of (∆BNO) = 10cm²
Therefore
Area of (∆BCO) = area of ∆BNO + area of ∆CNO
= 10cm² + 40cm²
= 50cm²
Therefore
Area of parallelogram CDPO = 2area of ∆BCO = 2 × 50 cm² = 100cm²
Now
Area of parallelogram ABCD/area of parallelogram BCPO = base DC × height/ base CP × height
DC/CP (both the parallelograms have the same height)
Therefore
Area of parallelogram ABCD/area of parallelogram BCPO = DC/BO
∆NBO and ∆NCD
∆NBO = ∆NCD and ∆BON = ∆NDC (BO // DC)
Therefore
∆ NBO ~ ∆NCD
Corresponding sides are proportional
So, NB/NC = BO/DC
Area of ABCD/Area of BCPO = NC/NB = 4/1
Area of parallelogram ABCD = 4 × 100cm² = 400cm²
Now, area of ∆CDO = ½ × area of parallelogram ABCD
= ¼ × 400cm²
100cm²
Area of ∆CDN = area (∆CDO) – are of CNO
= 100cm² – 40cm²
A = 60 cm²
Thus the area of the traingle CDN is 60 sq. cm
Example 10.
In the figure XQ//SY, PS //QR, XS//SYnqnd QY = 4cm. Find the area of ∆MSR and parallelogram PQRS?
Solution:
Area of ∆MSR = ½ × area of a rectangle of SR of height QY
= ½ × SR × QY
½ × 6 × 4cm²
= 8cm²
Area of ∆MSR = ½ × area of parallelogram PQRS
Therefore
9cm² = ½ × area of parallelogram PQRS
Thus the Area of parallelogram PQRS = 8 × 2cm² = 16cm²
Example 11.
The angle between any two sides of a parallelogram is 60 degrees. If the length of the two parallel sides is 4cm and 6cm respectively then find the area.
Solution:
Let a = 4cm and b = 6cm
x = 60 degrees
Area = ab sin(90)
Area = 24 sin90
Area = 24 × 1 = 24 square cm
Example 12.
Find the area of the parallelogram with the base of 2cm and the height of 6cm.
Solution:
Given that
Base = 2cm, height = 6cm
We know that
Area of parallelogram = base × height square units
= 2 × 6 = 12cm
Therefore the area of parallelogram = 12cm²
Example 13.
The base of the parallelogram is twice its height. If the area is 182 cm². Find the base and height.
Solution:
Let the height of the parallelogram = h cm
Then the base of the parallelogram = 3h cm
Area of parallelogram = 182cm²
Area of Parallelogram = base × height
Therefore 182 = 3h × h
3 × h² = 182
h² = 182/3
Hence the height of the Parallelogram is 182/3 cm and breadth is
Breadth = 3 × h
= 3 × 182/3
= 182cm
Example 14.
The area of a parallelogram is 400 square cm. Its height is twice its base. Find the height and base.
Solution:
Given that
Area = 400 square cm
Height = twice of base
h = 2b
We know that
Area = breadth × height
400 = breadth × 2b
2b² = 400
b² = 200
b = 14.1
Height = 2 × b = 2 × 14.1 = 28.2cm
Example 15.
Find the area of Parallelogram whose breadth is 4cm and height is 2cm.
Solution:
Given that
Breadth = 4cm
Height = 2cm
Area of Parallelogram = breadth × height
= 4 × 2cm²
= 8cm²