An isosceles triangle is a type of triangle that is having two sides of equal length, two equal angles. The sum of internal angles of a triangle is equal to 180°. Here we will learn about the properties of an isosceles triangle and problems on it from this page. The different types of questions and solutions on the isosceles triangle are along the lines.
Properties of Isosceles Triangle
Every isosceles triangle has the following properties.
- It has two sides of equal length.
- The unequal side of an isosceles triangle is called the base of the isosceles triangle.
- The angles opposite to the equal sides are equal.
- The angle which is not congruent to the two congruent base angles is called an apex angle.
- The altitude drawn from the apex bisects the base into two equal parts and also divides the apex angle into two equal angles.
- The altitude from the apex of an isosceles triangle divides the triangle into two congruent triangles.
- The perimeter of the triangle = the sum of all three sides.
- Area of an isosceles triangle = ½ x base x height.
Also, Read
- Angles Opposite to Equal Sides of an Isosceles Triangle are Equal
- Bisectors of the Angles of a Triangle Meet at a Point
- Sides Opposite to the Equal Angles of a Triangle are Equal
Examples on Properties of Isosceles Triangles
Example 1:
Find the area, perimeter of an isosceles triangle whose equal sides and base length is 5 cm, 6 cm respectively.
Solution:
Given that,
Two equal sides of an isosceles triangle a = 5 cm
length of the base b = 6 cm
Perimeter of an isosceles triangle = a + a + b
= 5 + 5 + 6 = 16 cm
Area of an isosceles triangle A = \(\frac { b }{ 2 } \) √(a² – \(\frac { b² }{ 4 } \))
= \(\frac { 6 }{ 2 } \) √(5² – \(\frac { 6² }{ 4 } \))
= 3 √(25 – 9)
= 3 x √16 = 3 x 4 = 12 sq cm
Therefore, the perimeter, area of an isosceles triangle is 16 cm, 12 sq cm.
Example 2:
Find x° from the below figures.

Solution:
In ∆ABC, AB = AC
According to the theorem, Angles Opposite to Equal Sides of an Isosceles Triangle are Equal
Therefore, ∠ABC = ∠ACB = x°
The sum of internal angles in a triangle is 180 degrees
So, ∠BAC + ∠ABC + ∠ACB = 180°
76° + x° + x° = 180°
76° + 2x° = 180°
2x°= 180°- 76°
2x° = 104°
x° = 104/2 = 52
Therefore, the value of x° is 52°.
Example 3:
If an isosceles triangle has lengths of two equal sides 15 cm, base 8 cm and altitude are drawn from the apex to the base of the triangle. Then find its perimeter and area.
Solution:
Given that,
Two equal sides are 15 cm, the base is 8 cm
The area of an isosceles triangle formula is ½ x base x altitude
So first, find the altitude.
We know that the altitude from the apex divides the isosceles triangle into two equal right angles and bisects the base into two equal parts.
Using Pythagorean theorem
Hypotenuse² = base² + perpendicular²
Altitude = √(15² – 8²)
= √(225 – 64) = √161
= 12.68
Area of triangle = ½ x 8 x 12.68
= 50.72 sq cm
Perimeter of isosceles triangle = 15 + 15 + 8 = 38 cm
Therefore, area and perimeter of an isosceles triangle are 50.72 sq cm, 38 cm respectively.
Example 4:
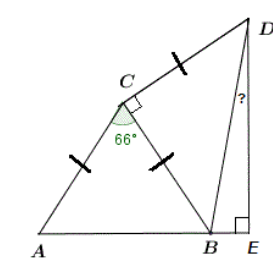
△ABC, △BCD are isosceles triangles. Find ∠BDE.
Solution:
Given that,
△ABC, △BCD are isosceles triangles.
Angles Opposite to Equal Sides of an Isosceles Triangle are Equal
So, ∠CAB = ∠ABC
∠CAB + ∠ABC = 180° – 66°
2∠ABC = 114°
∠ABC = 57°
△BCD is a right isosceles triangle
∠CBD = ∠CDB = (180 – 90)/2 = 45°
∠ABC, ∠CBD and ∠DBE make a straight angle
So, ∠ABC + ∠CBD + ∠DBE = 180°
∠DBE = 180 – ∠ABC – ∠CBD
= 180° – 57° – 45° = 78°
DBE is a right triangle
So, ∠BDE = 90 – 78 = 12°
Example 5:
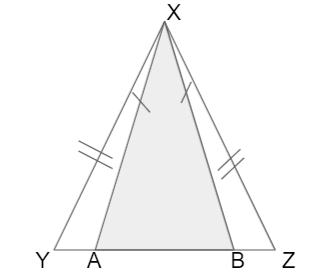
In the adjoining figure, it is given that XY = 4y, XZ = 7x, XA = 10x and XB = 12 + 2y. Find the values of x and y.
Solution:
Given that,
XY = XZ
4y = 7x
7x – 4y = 0 — (i)
XA = XB
10x = 12 + 2y
10x – 2y – 12 = 0 — (ii)
Multiply (ii) by 2
12x – 4y – 24 = 0 —- (iii)
Subtract (iii) from (i)
12x – 4y – 24 – 7x + 4y = 0
5x – 24 = 0
x = 24/5 = 4.8
Substituting x = 4.8 in (i)
7(4.8) – 4y = 0
33.6 = 4y
y = 8.4
Therefore, the values of x and y are 4.8, 8.4.
Example 6:
Find x° and y° from the given figure.

Solution:
In ∆XYP,
∠YXP = 180° – ∠QXY, as they form a linear pair.
∠YXP = 180° – 130°
∠YXP = 50°
It is given that, XP = YP
∠YXP = ∠XYP = 50°
The sum of three angles of a triangle is 180°
∠XPY + ∠YXP + ∠XYP = 180°
∠XPY = 180° – (∠YXP + ∠XYP)
∠XPY = 180° – (50° + 50°)
= 180° – 100°
∠XPY = 80°
Now, x° = ∠XPZ = 180° – ∠XPY (linear pair)
x° = 180° – 80°
x° = 100°
Also, in ∆XPZ we have,
XP = ZP
∠PXZ = ∠XZP = z°
Therefore, in ∆XPZ we have,
∠XPZ + ∠PXZ + ∠XZP = 180°
x° + z° + z° = 180°
100° + z° + z° = 180°
100° + 2z° = 180°
2z° = 180° – 100° = 80°
z° = 40°
Therefore, y° = ∠XZR = 180° – ∠XZP
y° = 180° – 40°
y° = 140°.