Radian is a measure of the trigonometric angle. The angle formed by an arc in a circle is exactly one radian and it is equal to the radius of the circle. We use radian as a unit of measuring angles in a circular system. Here we are giving the proof for the statement radian is a constant angle. Also, check example questions on expressing radian in the units of the sexagesimal system.
Prove that Radian is a Constant Angle
A radian is defined as an angle subtended at the center of a circle by an arc whose length is equal to the radius of that circle. Here is the proof for the statement i.e radian is a constant angle.
Let us take a circle with center O and radius r. Also, take any two points on the circle A, B and AB = OA = r, then by the definition ∠AOB = 1 radian.
Produce AO to intersect the circle at point C so that the length of arc ABC is equal to half of the circumference and ∠AOC, the angle at the center subtended by the arc = arc straight angle = two right angles.
\(\frac { arc AB }{ arc ABC } \) = \(\frac { r }{ ½ x 2πr } \) = \(\frac { 1 }{ π } \)
\(\frac { ∠AOB }{ ∠AOC } \) = \(\frac { 1 radian }{ 2 right angles } \)
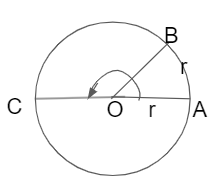
The arc of a circle is proportional to the angle it subtended at the center of the circle.
Therefore, \(\frac { ∠AOB }{ ∠AOC } \) = \(\frac { arc AB }{ arc ABC } \)
\(\frac { 1 radian }{ 2 right angles } \) = \(\frac { 1 }{ π } \)
So, 1 radian = \(\frac { 2 }{ π } \) right angles
Both 2, π are constants.
Hence, proved.
Also, Check
Example Questions & Answers
Question 1:
Express one radian in the units of the sexagesimal system.
Answer:
1 radian = 180°/(22/7)
= (180 x 7)°/22
= 57° 16′ 22″
Question 2:
Express 3 radians in the units of the sexagesimal system.
Answer:
3 radians = 540°/(22/7)
= (540 x 7)°/22
= 171°49’5″
FAQ’s on Radian Angle
1. Can radians be an angle?
A radian is a measurement unit for the angles. It is defined as the ratio of the length of the arc of a circle to its circle.
2. What type of angle is a radian?
A radian is a measurement unit for the circular system angles. It is mostly used in trigonometry.
3. Is radian equal to pi?
The exact value of 1 radian = 57.2958°.