You must have searched various sites to learn about Rectangular Cartesian Coordinates of a Point. Cartesian coordinates are the pair of numbers that specify the distance on the coordinate axis. Rectangular Cartesian Coordinates of a Point are defined by the ordered pairs x and y that indicate the points on the graph. Refer to our page to gather more information regarding the rectangular cartesian coordinates of a point. In addition to the concept of cartesian coordinates, the students can also find the solved examples on Rectangular Cartesian Coordinates of a Point from this article.
Also, See:
Rectangular Cartesian Coordinates of a Point – Definition
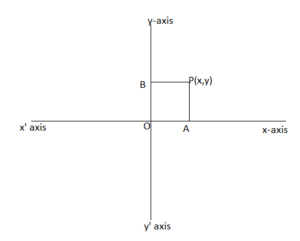
In order to find the rectangular cartesian coordinates of a point, you have to take two intersecting lines x-axis and the y-axis. They are perpendicular to each other which cuts at the origin O. Let P be the point in a plane. Draw the perpendicular lines from P to x-axis and P to y-axis. That point is M and N. Measure the lines PA and PB in a and b units. Here (a,b) are called the rectangular Cartesian coordinates of a point. The point P represents the position of the point in a plane.
Rectangular Coordinate System Examples with Answers
Example 1.
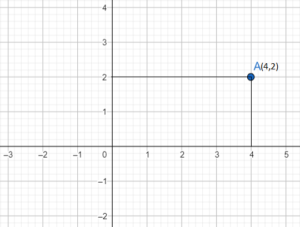
Find the new coordinates of the point (3,4) if the origin is shifted to the point (1,2) by translation of the axis.
Solution:
The given points are
(h,k)=(1,2) and (x,y)=(3,4)
Therefore new coordinates (X,Y)
x=X+h and y=Y+k
Therefore 3=X+1 and 4=Y+2
Which gives, X=4 and Y=2.
Hence, the new coordinates are (4,2)
Example 2.
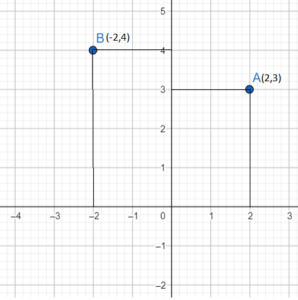
Plot the rectangular coordinates of the points (2,3) (-2,4).
Solution:
Given that
The first point is (2,3)
Here the x coordinate is positive and the y coordinate is also positive, so the point lies in the first coordinate and plots the graph using the points (2,3).
The second point is (-2,4).
Here the x coordinate is negative and the y coordinate is positive, so the points lie in the second quadrant and plot the graph using the points (-2,4).
Example 3.
Find the new coordinates of the point (5,6) if the origin is shifted to the point (3,7) by translation of the axis.
Solution:
The given points are
(h,k)=(5,6) and (x,y)=(3,7)
Therefore new coordinates (X,Y) .
x=X+h and y=Y+k
Therefore 3 = X+5 and 7 = Y+6
Which gives, X=2 and Y= -1
Hence, the new coordinates are (2,-1)

Example 4.
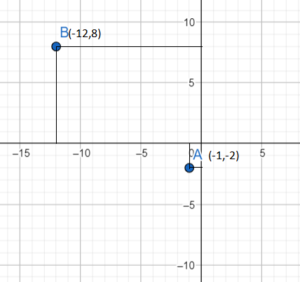
Plot the rectangular coordinates of the points (-1,-2) (-12,8)
Solution:
Given that
The first point is (-1,-2)
Here the x coordinate is negative and the y coordinate is also negative, so the point lies in the third coordinate and plots the graph using the points (-1,-2).
The second point is (-12,8)
Here the x coordinate is negative and the y coordinate is positive, so the points lie in the second quadrant and plot the graph using the points (-12,8).
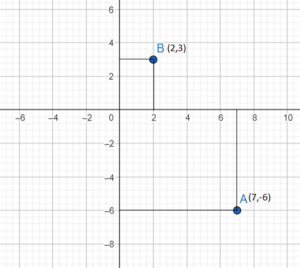
Example 5.
Plot the rectangular coordinates of the points (7,-6)
Solution:
Given that
The first point is (7,-6)
Here the x coordinate is positive and the y coordinate is negative, so the point lies in the fourth coordinate and plot the graph using the points (2,3).
Frequently Asked Questions
1. What is a rectangular Cartesian coordinate?
Cartesian coordinates are also called rectangular coordinates, it is a method of plotting graphs and pointing the positions of points on a two-dimensional surface or in three-dimensional space. The Cartesian plane consists of two perpendicular axes that cross the origin.
2. What is the point in rectangular coordinates?
In the rectangular coordinate every point is represented as an ordered pair. The first number in the ordered pair is called the x-coordinate, and the second number is called the y-coordinate.
3. How are polar coordinates and rectangular coordinates related?
Rectangular coordinates or cartesian coordinates come in the form of (x,y). Polar coordinates on the opposite hand, are available in the shape (r,θ). rather than moving out from the origin victimization horizontal and vertical lines, we tend to instead choose the angle θ, that is that the direction, then moves out from the origin a particular distance r.